无人驾驶车辆模型预测控制中的运动规划算法

研究无人驾驶车辆的运动规划问题时，利用感知系统提供的障碍物位置与运动属性、路面特性以及车辆本身状态，可计算出从当前位置到局部目标位置的没有碰撞的行驶轨迹。根据前面对路径规划与轨迹规划的特点介绍可知，一旦轨迹被确定了，车辆沿着路径的运动形式也就被确定了。轨迹规划既可以是在路径规划后的二次规划，也可以是根据感知信息所进行的一次规划。

1.路径规划算法约束条件

无人驾驶车辆的局部路径规划算法不同于一般移动机器人的路径规划问题。为满足车辆转向过程中的平稳性以及安全性需求，车辆运动微分约束和动力学特性约束是需要考虑的重要特征，同时还需要考虑车辆操纵稳定性及舒适性问题带来的控制约束。文献[26]利用弹性带理论(Elastic Band Theory)对无人驾驶车辆的紧急避障路径进行了规划，在规划时提出将路径的局部曲率变化最小作为约束条件，从而提高了车辆紧急避障时的操纵稳定性。文献[27]讨论了非结构化环境下基于滚动窗口的无人车辆路径规划问题，并在规划过程中考虑了车辆的安全约束。

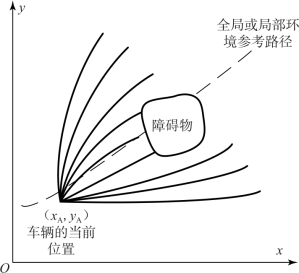
图1.3　基于5次多项式的路径规划

局部路径规划算法中考虑约束的一种思路是对车辆行驶曲线进行描述，通过设计评价函数选取不同工况下的行驶曲线完成规划。文献[16]利用5次多项式描述行驶曲线，将问题变为求取连接两个确定的目标点之间的曲线，并且满足目标点处有固定的航向角和固定曲率的要求，如图1.3所示；同时，在全局或者局部环境中的参考路径上用不同预瞄距离确定若干个预瞄位姿，对于每个预瞄位姿沿其法线方向按照不同横向位置偏差再确定若干个目标位姿，各目标位姿航向与预瞄位姿相同，计算当前车辆位姿和各目标位姿之间的行驶曲线作为候选曲线集合，行驶曲线需要满足车辆运动微分约束。候选曲线集合包含了用不同预瞄距离生成的行驶曲线，而对于同一预瞄距离处的多条行驶曲线，其目标位姿相对于期望路径是对称分布的。首先对各条行驶曲线进行碰撞分析，在行驶曲线上的每一位姿处增加车辆的宽度和长度信息，与构形空间中的障碍物检测结果进行对比，判断行驶曲线与障碍物发生碰撞的位置，仅保留此位置以前的行驶曲线。然后，在具有相同横向位置偏差的行驶曲线中保留最长的一条用于路径评价。经过碰撞安全性分析，在每个横向位置偏差仅保留了一条满足横向安全和路径跟踪要求的行驶曲线。车辆的实际驾驶行为，如跟随或超车，则通过选择一条行驶曲线作为待执行路径来实现。

德国卡尔斯鲁厄大学在DARPA Urban Challenge的参赛车辆AnnieWAY上采用了基于触须原理的局部路径规划算法[28]，利用多组不同半径的圆弧描述不同车速下的行驶路径，如图1.4所示。文献[18]对该算法进行了改进，使之适用于全局环境未知的智能车自主行驶，但由于它在进行触须生成时采用圆弧曲线，而忽略了车辆转弯半径的变化，故在车速较快时容易发生跟踪失败的情况。这也说明在高速时还需要进一步考虑车辆动力学特性的约束。

文献[29]结合预测控制理论进行了无人车辆的局部路径规划。借鉴预测控制的滚动优化原理，提出了基于滚动窗口的移动机器人路径规划方法。该方法在全局环境未知时能够充分利用已探知的局部信息，有效地结合优化与反馈机制，不仅使局部规划的计算量保持在较低水平，而且保证了全局的收敛性，获得了较好的规划效果。文献[30]同样借鉴了滚动优化的原理，提出了一种带约束曲线拟合的路径规划方式，如图1.5所示。该方法通过在规划中引入几何约束，如起始位姿约束、最小转弯半径约束等，有效地避免了在跟踪过程中同时考虑位置和航向误差的问题。

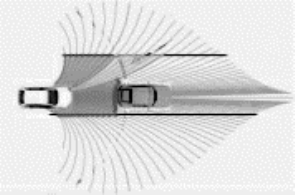
图1.4　基于触须原理的路径规划　

图1.5　带约束曲线拟合的路径规划

2.轨迹规划算法约束条件(www.xing528.com)

轨迹规划问题一般是在考虑系统某项性能最优的同时，加入边界约束、环境几何约束以及系统的动力学约束等非线性约束，最终构成一个非线性最优化问题。因此，轨迹规划的主要研究方向集中在非线性最优求解和约束条件等价转换上。轨迹规划问题一般无法找到显式解，普遍的做法就是将这一优化问题转换为非线性规划问题，进而通过相应的非线性规划求解器求解。

文献[31]采用直接法，利用多项式直接对系统状态进行参数化，进而将轨迹规划问题转换为数学规划问题。文献[32]在借鉴样条法原理的基础上，通过局部近似的方法构建全局连续的优化轨迹。虽然这种转换解决了在轨迹空间优化的难题，但是其优化的速度依赖于参数空间的维度。为此，Fahroo等人在对非线性系统平坦性研究的基础上，给出了平坦系统的轨迹规划方法[33]。其主要优点就是通过系统的平坦性将高维度空间的参数优化问题降为低维度参数空间的优化问题，从而提高了优化速度。文献[34][35]也应用微分平坦理论对不同形式的机器人进行了轨迹规划方面的研究。

侧倾约束下的运动规划也是高速运动车辆需要考虑的一个重要约束。侧倾主要采用横向载荷转移率(LTR)、侧倾角和横向加速度作为判断标准。文献[36]在被动侧倾控制基础上进行了模型预测改进运动规划；文献[52][63]在机器人车辆运动轨迹规划时，设计了车辆动力学参数值窗口，采用了速度-曲率轨迹方法计算运动轨迹。由于采用的窗口值只考虑曲率，所以其计算速度快，但并不具备车辆控制稳定的最优性。

在约束条件处理方面，基于简化运动学模型满足车辆非完整约束的方法比较普遍[37，38]。假设车辆在运动过程中没有滑移，那么就是非完整(Nonholonomic)动力学约束，但是这种方法不适用于高速行驶车辆，因为此时车辆的约束已经不再局限于非完整约束，车辆的横向动力学成为规划中必须考虑的因素。文献[39][40]在考虑车辆动力学约束情况下对车辆的行驶轨迹进行了规划，实现了连续曲率的轨迹规划。

图1.6　点质量模型受力分析

为了减少动力学约束的复杂程度，忽略车辆尺寸信息简化而来的点质量模型也在轨迹规划中得到了应用[41-43]。其受力分析如图1.6所示。从图1.6中可以看出，该模型考虑了车辆的侧向受力，并且将约束条件转换为加速度圆(Acceleration Circle Constraint)。应用该模型能够顺利完成避障任务。点质量模型相比于普通自行车模型计算量更小，可以有效地减少车辆非线性动力学模型的复杂性。将车辆动力学模型近似为点质量模型，同时将轮胎摩擦圆约束也映射到加速度约束上，以及其他的一些技巧，均可用于简化计算。

3.运动规划算法及存在的问题小结

从上面介绍可以看出，轨迹规划方面的研究一般都按照局部路径规划方法进行，然后在考虑多种约束条件的情况下对其进行轨迹化。与低速行驶的移动机器人不同的是，无人驾驶车辆的路径规划和轨迹规划更多采用多项式行驶曲线的方式进行拟合，同时考虑了执行机构的约束。这种规划的特点是能够保证车辆平顺行驶，不会出现突然转向。为了进一步提高系统的实时性，微分平坦、点质量模型等相关理论也被应用在了轨迹规划的过程中。

普通规划方法在高速无人车辆运动规划中普遍存在的问题是实时性达不到要求，特别是紧急情形下的危险规避运动规划对实时性要求更高。基于动力学优化模型的规划方法均考虑了轮胎摩擦圆约束，采用受加速度约束的点质量模型对轮胎摩擦圆约束做了近似处理，但没有对高速车辆动力学模型结合运动规划做深入的最优分析。对侧倾约束下运动规划方法的研究较少，且主要集中在越野环境，仅仅是根据阈值窗口范围进行运动规划，也同样没有根据车辆动力学理论的稳定性最优原则产生运动轨迹。此外，同时考虑滑移与侧倾的研究则更少。

点质量模型最优控制特性分析也是运动规划中的一个重要因素。用加速度值有界且方向可控的点质量模型进行最优控制特性分析和证明，能保证建立在此基础上的相关算法的可靠应用。Bryson和Ho给出了几种情形的证明并且将其应用到运载火箭的发射中，用于推力控制分析中[44]，可以供地面车辆的运动规划最优特性分析参考。