大学物理实验报告一般式样举例-附录

金属丝杨氏模量的测定

【实验目的】

（1）掌握用光杠杆装置测量微小长度变化的原理和调节方法；

（2）学会用拉伸法测量金属丝的杨氏模量；

（3）学会用逐差法处理数据.

【实验原理】

一根均匀的钢丝（设长度为L，直径为d），在受到沿长度方向的外力F作用下发生形变，伸长了△L.根据胡克定律，在弹性限度内，胁强与胁变成正比，即

又截面积，整理后，该钢丝的杨氏模量E由下式表示：

式中，△L是一个微小的长度变化量，很难用普通测量长度的仪器测准确，本实验中，用光杠杆装置进行放大测量.光杠杆放大原理如图A-1所示.

图A-1　光杠杆原理图

由图A-1中的几何关系，可近似地有

将式（A-2）代入式（A-1），得

这就是本实验用来测定杨氏弹性模量的原理公式.式中，E为钢丝的杨氏弹性模量（N·m-2）；F为作用在钢丝轴向上的外力（N）；L为钢丝的原长（m）；R为镜面至标尺的距离（m）；d为钢丝的直径（m）；D为光杠杆常数（光杠杆后足尖至两前足尖连线的垂直距离）（m）；l为挂重物前后标尺读数的差值（m）.

【实验仪器】

杨氏模量仪、望远镜及标尺、螺旋测微计、直尺、卷尺、砝码等.

【数据记录与处理】

1.用逐差法处理数据

（1）将数据填入相应的表格中（表A-1，表A-2，表A-3），并用逐差法计算l.

表A-1　标尺读数测量数据表(www.xing528.com)

表A-2　金属丝直径测量数据表

注：量具：螺旋测微计， Δ仪=0.004mm.

表A-3　L，R，D测量数据表

注：L，R，D都是单次测量，且标志线位置较难确定，对应的不确定度值由实验室给出.

（2）计算杨氏模量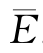

（3）计算杨氏模量的不确定度

杨氏模量的测量结果为

2.用作图法处理数据

式（A-3）可改写为

式中，.若作l-F图线，且为直线，求出斜率K，就可得

由表A-1可列出表A-4：

表A-4

以F为横轴，l为纵轴，作得l-F图线，见图A-2.

图A-2　l-F图

由图线得到斜率

代入式（A-5），得

【讨论】（略）

讨论内容一般不受限制，可以对实验现象进行评述，对结论和误差原因进行分析，也可以对实验提出改进意见.