用牛顿环测量曲率半径的光干涉实验成果

光的干涉现象是光波的基本特性之一.在对光的本性的认识过程中，它为光的波动性提供了重要的实验证据.光的干涉现象在科学研究和工程技术上有着广泛的应用.如测量光波波长，测量微小物体的长度、厚度和角度，检验加工物体表面的光洁度，测定材料的折射率等.

本实验利用光的干涉现象测量平凸透镜的曲率半径.

【实验目的】

（1）观察光的等厚干涉现象；

（2）用牛顿环测量平凸透镜的曲率半径；

（3）掌握读数显微镜的使用方法；

（4）掌握用逐差法处理数据.

【实验原理】

牛顿环仪是由曲率半径较大的平凸透镜与平面玻璃组成，如图3-8-1所示.在透镜的凸面和平面之间形成一层空气薄膜，厚度从中心接触点到边缘逐渐增加.当平行的单色光垂直入射时，入射光将在此薄膜上下两表面反射，产生具有一定光程差的两束相干光.由于透镜的一面为球面，所以，光程差相等的各点连起来的轨迹是一个以接触点为中心的圆，因此，形成的干涉条纹是一个以接触点为圆心的一系列明暗相间的同心圆环，如图3-8-2所示.这样一族圆环形的干涉条纹叫做牛顿环.

设R为平凸透镜的曲率半径，r为牛顿环某环的半径，e为半径r处空气薄膜的厚度，λ为入射光的波长.透镜下表面所反射的光1与玻璃平板上表面所反射的光2发生干涉，两束光的光程差为

式中，为附加光程差.它是由于光从光疏媒质（空气）射向光密媒质（玻璃）的交界面上反射时，发生半波损失而引起的.

由图3-8-1中的几何关系可得

由于e≪R，所以，e2≪2Re，可将e2从上式中略去，即

图3-8-1　牛顿环光路图

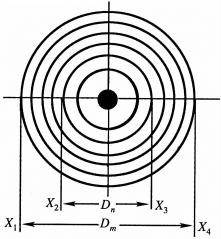
图3-8-2　牛顿环

将式（3-8-2）代入式（3-8-1），得

根据干涉加强和减弱条件，有

亮环：

暗环：

为了便于观察，选暗环为观察对象，当干涉条纹为暗环时，有

由式（3-8-3）可见，当k=0时，r=0，接触点为暗点.在已知单色光波长λ的情况下，只要测量暗环的半径r和暗环的级数k，就可算出透镜的曲率半径R.但由于接触点处机械压力引起玻璃的弹性形变，以及接触点处不十分干净（有灰尘等），使得接触点不可能是一个理想点，而是一个明暗不清的模糊圆斑，这样，在测量时，就无法确定暗环的级数，也无法精确测量暗环的半径，因此，直接用式（3-8-3）测量曲率半径R，会带来较大误差.为此，通常取两个暗环的直径的平方差来计算R.

设第m级暗环和第n级暗环的直径分别为Dm和Dn，根据式（3-8-3），有

将两式相减，得

即

式（3-8-4）表明，两暗环直径的平方差只与它们相隔几个暗环的数目（m-n）有关，而与它们各自的级数无关.因此，测量时，我们就可以用环数代替级数，从而避开了难以确定级数k、难以精确测量半径r的困难，提高了测量的精确度.这是物理实验中常用的处理方法.

由式（3-8-4）可见，在已知单色光波长λ的情况下，只要测出第m条暗环的直径Dm、第n条暗环的直径Dn和环数差（m-n），即可计算出透镜的曲率半径R.

【实验器材】

读数显微镜、牛顿环、钠光灯.

整个实验装置如图3-8-3所示.图中的读数显微镜是一种测量物体微小尺寸或微小距离变化的仪器.它是由一个带十字叉丝的显微镜和一个螺旋测微装置所组成的.显微镜包括目镜、十字叉丝和物镜.整个显微镜与套在测微螺杆的螺母管套相固定.当转动测微鼓轮时，测微螺杆推动显微镜和主尺的读数刻线沿主尺移动.主尺每一格为1mm，测微鼓轮圆周等分100小格，测微鼓轮转动一周，主尺的读数刻线沿主尺移动1mm，因此，测微鼓轮上一小格代表0.01mm，可估读到千分之几毫米.读数方法与螺旋测微计相同.(www.xing528.com)

图3-8-3　测量牛顿环装置图

1—测微鼓轮；2—调焦手轮；3—目镜；4—钠光灯；5—平面玻璃；6—物镜；7—45°玻璃片；8—平凸透镜；9—载物台；10—支架；11—锁紧螺钉

【实验内容与步骤】

1.目测观察牛顿环仪的干涉条纹

仔细调节牛顿环仪的三个螺丝，目测观察，使干涉条纹稳定地处于牛顿环仪的中央位置，并使牛顿环条纹中心点最小.

2.调节读数显微镜

（1）照明

按图3-8-3安置好实验仪器.将读数显微镜的物镜对准牛顿环仪的中央.移动读数显微镜，对准钠光灯源，同时微调45°平面反射玻璃片，使钠光灯发出的单色光经45°平面反射玻璃片反射后垂直向下入射到牛顿环上，使视场最亮.

（2）调焦

①旋动目镜，改变目镜与叉丝之间的距离，直到能清晰地看清叉丝为止.

②将读数显微镜的物镜靠近待测的牛顿环仪，旋转调焦手轮，改变牛顿环仪与物镜之间的距离，使牛顿环通过物镜成的像恰好在叉丝平面上，直到在目镜中能同时看清叉丝和放大的牛顿环的像为止.

3.用读数显微镜观察牛顿环仪的干涉条纹

转动测微鼓轮，左右移动显微镜，观察牛顿环条纹的特征.

4.测牛顿环直径

（1）转动测微鼓轮，使显微镜移动，观察十字叉丝是否有一条与镜筒移动方向垂直，而另一条与镜筒移动方向平行（即与标尺平行），若不符，则松开锁紧螺钉，适当旋动目镜筒，使之达到上述状态.

图3-8-4　测量暗环直径示意图

（2）转动测微鼓轮，从牛顿环中心向左按顺序数到第25环（暗环），再反向转退到m=20环，使叉丝与暗环的外侧相切，如图3-8-4所示，记录标尺读数.继续转动鼓轮，使叉丝依次与牛顿环左方第19，18，17，16，15，14，13，12，11环的外侧相切，记下相应的读数.再继续转动测微鼓轮，使叉丝经过牛顿环中心并依次与右方第11，12，13，14，15，16，17，18，19，20环的内侧相切，记下相应的读数.在测量时，要格外小心，测微鼓轮应沿一个方向旋转，中途不得反转，以免螺距空程引起误差.

注意：

（1）在测量牛顿环直径的过程中，为了避免螺距空程误差，测微鼓轮只能单方向移动.

（2）开始测量时，先数到第25环再反向转退到m=20环，是为了避免螺距空程误差.

（3）先使叉丝与左方的暗环外侧相切，再与右方的暗环内侧相切，是因为牛顿环条纹有宽度.

（4）读数显微镜在调节中要防止其物镜处的45°玻璃片与牛顿环仪相碰，以免损坏仪器.

【数据记录与处理】

（1）将实验测得的数据填入表3-8-1中，m-n=5，用逐差法计算平均值

表3-8-1　数据测量表

（2）已知钠光波长λ=5.893×10-4mm，根据下式计算透镜的曲率半径：

自学提纲

1.牛顿环中心会不会出现明斑？为什么？对测量有无影响？

2.为什么不利用r2=kRλ测量R？

3.为什么牛顿环相邻两暗环（或亮环）之间的距离靠近中心的要比靠近边缘的大？

4.简述读数显微镜的调节步骤.

5.在使用读数显微镜测量牛顿环直径的过程中，为了避免螺距空程误差，应注意什么？

6.在测量时，若十字叉丝交点不通过圆环中心，则测量的是弦而不是直径，问对实验结果有否影响？为什么？

7.本实验能否用作图法计算R？如何作图？如何计算？