大学物理实验：作图法的应用与优点

1.作图法的作用和优点

作图法是一种被广泛用来处理实验数据的方法.物理量之间存在的关系既可以用解析函数表示，也可以用图线表示.科技工作者一般对图线很感兴趣，因为图线能形象直观地表明两个变量之间的关系.特别是对那些尚未找到适当解析函数表达式的实验结果，可以从画出的图线中寻找相应的经验公式.此外，作图法还可以求出函数式中相应的参量和其他待测量.

作图法处理数据并不复杂，但对许多初学者来说，却是比较困难的.这是由于初学者缺乏作图的基本训练，也可能是由于思想上对作图不够重视.相信只要认真对待，一定能熟练掌握作图法这种重要的数据处理方法.

2.作图规则

在作图前，一般先将相关数据列成表格形式，这是作图的依据.

（1）选用坐标纸.最常用的是线性直角坐标纸（毫米坐标纸），根据需要，也可选用单对数坐标纸、双对数坐标纸、极坐标纸等.坐标纸的大小一般应根据所测数据的大小、有效数字的多少以及结果的需要来确定.

（2）确定坐标轴.一般以横轴代表自变量，纵轴代表因变量.在坐标纸的左方和下方画出两条粗细适当的线表示纵轴和横轴，在轴的末端外侧标明所代表的物理量符号和单位.

（3）确定坐标轴的比例与标度.要适当选取横轴和纵轴的比例及坐标起点，使图线充满整张坐标纸，不偏于一角或一边.确定比例及标度时应注意：

a.原则上，图中实验点的坐标读数的有效数字位数不能少于实验数据的有效数字位数.也就是说，数据中的可靠数字在图中是可靠的，数据中可疑的一位在图中是估计的.

b.一般地说，轴上每一小格所代表的量值应为1，2，5，而不应为3，7，9等.这样，对于描点和读坐标将很方便.在轴上应等间距进行标度，力求简明，以不用计算就能方便地直接读出图线上每一点的坐标为宜，通常也用1，2，5，而不选用3，7，9来标度.

c.横轴和纵轴的标度可以不同，两轴的起始点也不一定都从零开始，可以取比数据最小值稍小一些的数作为起始点，以便调整图线的大小和位置.

d.如果数据特别大或特别小，可以提出数量级，例如提出“×103”或“×10-2”，写在坐标轴物理量单位符号前面.

（4）标点与连线.用削尖的硬铅笔以小“+”字标在坐标纸上，应使“+”交叉点正好落在测量数据所对应的坐标上.当一张坐标纸上要画几条图线时，每条图线可采用不同的标记，如“×”“△”“⊙”等，加以区别.连线时，要用直尺或曲线板，根据不同情况，把数据点连成直线或光滑曲线.图线并不一定要通过所有的点，而是让数据点大致均匀地分布在所画图线的两侧，并尽量靠近图线.如欲将图线延伸到测量数据的范围之外，则应依其趋势用虚线来表示.

在实验中，还常常遇到一种曲线，称为校正曲线，例如，用精度等级高的电表校正精度等级低的电表作的曲线.作校正曲线时，相邻数据点一律用直线连接，成为折线，而不能连成光滑曲线.

（5）写图注说明.在图的空处（一般在图纸上部）写清图名及必要的说明，如横轴为x轴，纵轴为y轴，则图名可为“y-x图”，所写字体，一般用仿宋体.

3.作图法求解参数

若由实验数据所画的y-x图是一条直线，则两物理量x，y应满足线性关系y=kx+b，其中，参数k和b可用作图法求得.

实验数据范围内，在直线上靠近两端内侧处取两点P1（x1，y1）和P2（x2，y2），其中，x的坐标最好为整数，并注意不要取原始实验数据点，用与实验数据点不同的符号将它们标示出来，并在旁边注明其坐标读数.

将P1（x1，y1）和P2（x2，y2）两点的坐标代入关系式y=kx+b中，有

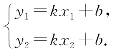
求解上列方程组，可得

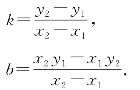
如果x轴的起点为零，则x=0时，y=b，故可直接从直线上读取b值.在数学上，k和b分别为y=kx+b的斜率和截距，而在物理上，k和b有其特殊的物理意义.

4.曲线改直

有些物理量之间的关系不是线性的，可通过适当变换使其变成线性关系，即把曲线改为直线，这样便可用上述方法求解相关参数.例如y=aebx，此关系式中a，b均为常数，显然，y-x图是一条曲线.如果两边取自然对数，可得lny=bx+lna，以x为横坐标，lny为纵坐标作图，即可得一直线，在此直线上取两点，把坐标代入上式即可求得常数a和b.(www.xing528.com)

下面举两个具体例子，说明如何作图，如何求解参数，如何把曲线改成直线，请仔细阅读.

例3 金属条长度L与温度t满足关系式L=L0（1+bt），式中，b为金属条的线胀系数，L0为0℃时金属条的长度，实验测得一组不同温度下的金属条长度，具体数据列表1-5-1，试用作图法求解b与L.

表1-5-1　不同温度下的金属条长度数据表

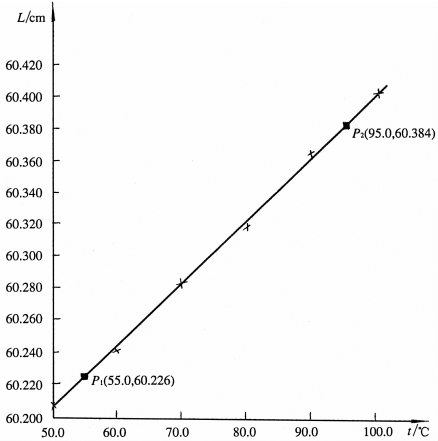
图1-5-1　金属条的L-t图线

解 根据上表数据，以温度t为横轴，以金属条长度L为纵轴作图，见图1-5-1，在直线上取两点P1（55.0，60.226）和P2（95.0，60.384），把两点坐标代入关系式L=L0（1+bt）中，

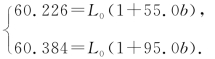
解此方程组，得

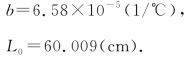
例4 在阻尼振荡实验中，电压幅值按指数衰减（u=u0e-βt），每隔一个周期（T=1s）测得电压，见表1-5-2.试用作图法求β和u0.

表1-5-2　不同时间测得的电压数据表

解 显然u与t之间的关系不是线性关系，将u=u0e-βt式取对数，有

用单对数坐标纸作图，得u-t图线，此图线为一直线，如图1-5-2所示，直线的斜率k=-β.

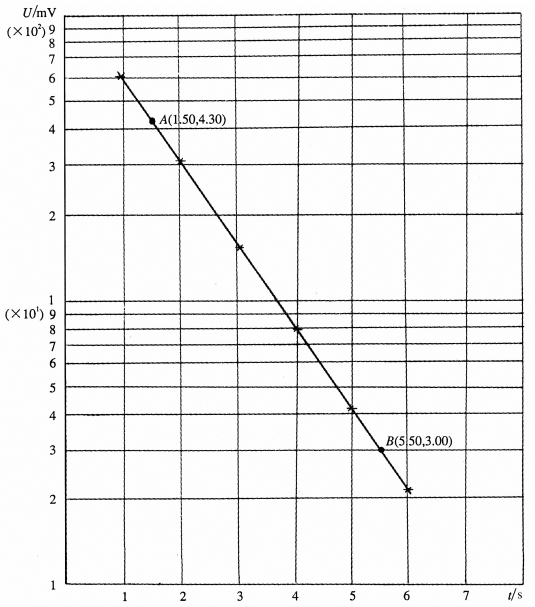
图1-5-2　用单对数坐标纸作U-t图线

在直线上取两点A（1.50，4.30）和B（5.50，3.00），可得直线斜率为

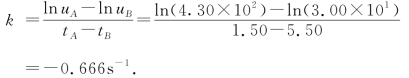
故

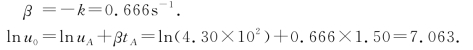
故

注意：单对数坐标纸是对数坐标纸中的一种，常用的还有双对数坐标纸.对数轴上的标度值是真数N，轴上某点到原点的距离与该点标度值N的对数是成正比的，轴上每一组“1，2，3，…，10”称为一个“级”，它可以容纳同一个数量级的数据，图1-5-2是一张二级单对数坐标纸.