为了使求得的测量结果保持应有的精度，又能简化运算过程，有效数字的计算应按一定的规则进行.在间接测量中必然要遇到有效数字的运算，测量值的有效数字一般由不确定度的量级来决定，也即先计算出不确定度，然后按前述“末位对齐”规则决定测量值的有效数字.而对于没有要求给出不确定度的测量值，在运算时则按以下几种运算规则确定有效数字位数.
1.加减运算
规则：几个数相加减时，其结果在小数点后所应保留的位数与各数中小数点后位数最少的一个相同.
例如（加下划线的数字代表可疑数字）：
2.乘除运算
规则：几个数相乘除时，某结果保留的有效数字位数与各数中有效数字位数最少的一个相同.
例如：
3.乘方、开方运算
乘方与开方的结果，其有效数字位数与其底的有效数字位数相同.
4.对数运算
对数函数运算后的尾数与真数的有效数字位数相同.
例如：
lg1.897=0.27806733，取成0.2781.
lg1897=3.278067331，取成3.2781.
5.三角函数运算
三角函数运算后的有效数字与角度的有效数字位数相同.
例如，sin36°56′=0.600885361，取成0.6009.
对其它函数运算，有一种简单直观的方法确定有效数字，即将自变量可疑位上下变动一个单位，分析函数结果在哪一位上变动，结果的可疑位（即末位）就取在该位.
应强调几点：
（1）运算公式中的某些数字是绝对准确数字，如
-中的倍数2，它不是测量得来的.没有可疑数字，T的有效数字位数由L与g的有效数字位数来决定.
（2）在运算过程中，我们还常常碰到一些常数，如π，一般取这些常数与测量值的有效数字位数相同，也可多取一位，例如，圆周长L=2πR，测量值R=2.186mm，则π应取3.142，也可取3.1416.
（3）如果某一间接测量值的计算比较复杂，有几个计算步骤，那么，中间步骤的运算结果可按运算规则确定有效数字位数后，再多保留一位，以免误差累积.
（4）一般情况下，应使用计算器进行运算，对其计算所显示的结果，必须按有效数字运算规则进行取舍，应特别注意，不要认为结果取位越多越好.
总之，在科学实验中，有效数字包含很重要的意义，我们应该学会正确合理地取舍数据，并进行科学的计算.数据取舍规则的采用，目的是保证测量结果的准确度不因数字取舍不当而受影响，同时，也可避免因保留一些无意义的可疑数字而做无用功.虽然，由于计算器的普及，计算器可以给出8到10位数字的计算结果，多取几位并不花费多少精力，也并不带来多少困难，但是实验结果的正确表达仍然值得重视，实验者应该学会正确判断实验结果是几位有效数字，以及如何科学合理表达实验结果.
下面两个例题综合了有效数字取舍、直接测量的不确定度评定、不确定度合成、间接测量的不确定度传递、测量结果表达等各方面知识，请读者仔细阅读，认真分析.
例1 用螺旋测微计（△仪=0.004mm）测量某圆柱体的直径6次，用游标卡尺（△仪=0.02mm）测量同一圆柱体的高度6次，数据见表1-4-1，试求圆柱体的体积和不确定度，并写出体积的测量结果.
表1-4-1 圆柱体尺寸
(www.xing528.com)
解 按以下步骤计算：
（1）计算圆柱直径D的平均值、A类不确定度、B类不确定度及合成不确定度
（备注：以上各量的计算为中间过程，结果宜多取一位，以减小计算中的舍入误差.）
（2）计算圆柱高h的平均值、A类不确定度、B类不确定度及合成不确定度
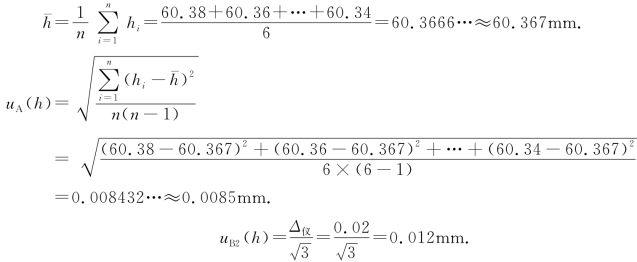
（备注：以上各量的计算为中间过程，结果宜多取一位，以减小计算中的舍入误差.）
（3）计算圆柱体积V的测量值、不确定度，并表达测量结果
圆柱体积的测量值为
根据不确定度传递公式，圆柱体积测量的不确定度为
圆柱体积的测量结果：
体积测量的相对不确定度
例2 假设例1中的圆柱体是铜制的，现用物理天平（感量0.1g，允差Δ仪=0.1g）采取复称法测量此圆柱质量1次，测得m=117.72g，求铜的密度测量值和不确定度，并写出测量结果.
（备注：题中的“复称法”是物理天平精确测量物体质量的方法，该方法将待测物体分别放在左、右盘上各测一次，得到质量m1，m2，用
算出物体质量，复称法能消除天平不等臂所引起的误差）
解 由圆柱质量及例1求得的体积测量值，铜密度的测量值为
圆柱质量的不确定度作简化处理，只考虑仪器不确定度uB2（x），
由不确定度传递公式，铜密度测量的不确定度为
所以，铜密度的测量结果为
铜密度测量的相对不确定度
请读者注意，应学会使用计算器的统计功能，可方便计算多次测量的不确定度.在阅读以上两个例题时，一方面要把重点放在计算方法和有效数字取位等内容上，同时建议用计算器认真算一遍.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
