大学物理实验有效数字的一般概念

1.有效数字的位数与所用仪器的精度有关

测量皆有误差.例如，我们用最小刻度为1mm（即分度值为1mm）的尺子测量某物体的长度，如图1-4-1（a）所示，可以看出，此物体的长度大于1.6cm，小于1.7cm，即长度在1.6cm到1.7cm之间，那么，到底是多少呢？我们可以通过目测进行估计，此物体的长度为1.62cm.这里，“1.6cm”是直接从尺上读取的，称为可靠数字，而最后一位“0.02cm”是从尺上估计出来的，是有误差的，称为可疑数字（尽管可疑，但还是有一定依据的，是有意义的，是不能省略的）.我们把可靠数字和可疑数字合起来，称为有效数字.所以，1.62cm一共有三位有效数字.应该强调，用这把尺子测量这个物体的长度时，只能读出三位有效数字，这是由这把尺子的测量精度决定的.如果我们用其他测量精度较高的仪器（如分度值为0.02mm的游标卡尺）测量此物体的长度时，测得数值的有效数字应有四位，例如为1.616cm，这里，“1.61cm”是可靠数字，而最后一位“0.006cm”是可疑数字.如果用精度很差的尺子（如用最小刻度为1cm的尺子）测量，则结果可能为1.6cm，只有两位有效数字.由此可见，有效数字的位数与测量仪器的精度有关.一般说来，测同一对象时，所用仪器的精度越高，测得的有效数字越多.

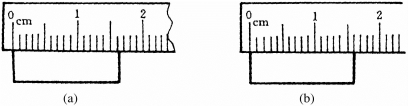
图1-4-1　长度的测量

2.末位为“0”和数字中间出现“0”都属于有效数字

我们再来看图1-4-1（b）的情况.如果物体的末端正好与刻度线对齐，估读的一位是“0”，是可疑数字，这个“0”也是有效数字，不能省略，读数应为1.60cm，它表示测量误差在位上.它与1.6cm是不同的，因为后者表示测量误差只在位上，最后一位“0.6cm”是可疑数字.所以，前者是三位有效数字，后者是两位有效数字.对于数字中间出现的“0”，例如30.308cm，显然是五位有效数字.

3.作十进制单位变换时，有效数字保持不变

例如，测量值1.80m，可以写成0.00180km，也可写成180cm，它们都是三位有效数字，都表示测量误差在位上，但是不能写成1.8m或0.0018km或1800mm，因为前两者只有两位有效数字，而后者有四位有效数字，它们表示的测量误差位有了变化，都没有如实地反映测量精度.(www.xing528.com)

为了书写规范，当数值特大或特小时，我们可采用如下的标准形式，即用10的幂方来表示数量级，前面的数字是测得的有效数字（常使小数点前取一位数字）.例如0.00352m，写成标准形式是3.52×10-3m.在进行单位变换时，用标准形式会很方便，例如3.8km=3.8×103m，不能写成3800m；4600Ω=4.600×103Ω=4.600kΩ，不能写成4.6kΩ.

4.尾数取舍修约规则

有效数字尾数的修约规则，应按现在通用的“四舍六入五凑偶”进行，即尾数小于5则舍，大于5则入，等于5时，前一数是偶数则舍，前一数是奇数则入，例如：

5.测量结果有效数字位数的确定

计算工具上显示的计算结果一般都有很多位，为了合理表示测量结果，需进行取舍.在1.3.4节中已提到，测量结果的表示有具体规范，在这里再作说明.在需要按式（1-3-6）表达测量结果时，首先不确定度取一位或二位有效数字（首位数为1或2时，最好取二位有效数字），其次再确定被测量平均值的有效数字，其末位与不确定度的末位对齐.相对不确定度取一位或二位有效数字（首位数为1或2时，最好取二位有效数字）.若是作为间接测量的中间结果，不确定度最好取二位有效数字.在截取尾数时，不确定度“只进不舍”，这是为了保证其置信概率水平不降低，而平均值则按有效数字修约规则取舍.

如长度测量值为12.346mm，不确定度为0.32mm，置信概率约为68.3%，则该长度测量结果表达为（12.35±0.32）mm（P≈68.3%），相对不确定度为2.6%；或者表达为（12.3±0.4）mm（P≈68.3%），相对不确定度为4%.