从上面分析可见，在消除或修正了系统误差的情况下，当测量次数n→∞时，随机误差满足正态分布规律，测量值的离散性用标准误差σ表述，即误差以一定的概率出现在用σ表述的某一区间内.而实际上测量次数总是有限的，显然不满足正态分布的条件，此情况下，随机误差遵从“t分布”规律.t分布是“准”正态分布，函数很复杂，在此不作介绍，其分布曲线与正态分布曲线的差别如图1-2-3所示.显然，在有限次测量的情况下（t分布），要保持同样的置信概率，就要扩大置信区间.当n→∞时，t分布趋向于正态分布.
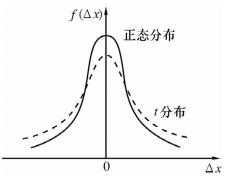
图1-2-3 t分布与正态分布的比较
对某一物理量进行n次等精度测量，得到测量列x1，x2，…，xn真值A的最佳估计值就是测量列的算术平均值：
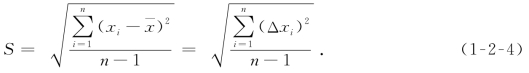(www.xing528.com)
式（1-2-4）称为贝塞尔（Bessel）公式，是后续计算不确定度时很有用的公式.显然，当n→∞时，S→σ，S是无限次测量的标准误差σ在有限次测量时的最佳估计值.
与正态分布的标准误差σ一样，标准偏差S也有类似的统计学意义，当测量次数足够多时，测量列中任一测量值与平均值之差落在[-S，+S]区间的概率是68.3%.S表征测量结果的离散性，S越大，表示测量值越分散，即测量精密度越大，随机误差越大；S越小，则反之.
在t分布理论中，有个系数t，称为置信系数，或称t因子，在置信概率P和测量次数n确定后，置信系数可从专门的数值表中查到.这里仅列出置信概率P=0.683时，不同测量次数n所对应的置信系数t的数值.
表1-2-1 P=0.683时，不同测量次数n下的置信系数t值
从表1-2-1中可以看出，置信系数t随测量次数的增加而趋向于1，可理解为n→∞时，t分布趋向于正态分布.在测量次数很少时，要用t值修正，才能更准确地表示测量结果.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
