大学物理实验：随机误差的正态分布

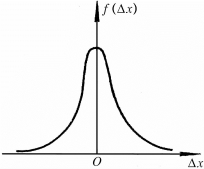
图1-2-1　正态分布的误差曲线

从某一次测量来看，随机误差的出现是偶然的，当测量次数足够多时，随机误差就会显示出明显的规律性.大量的实验事实和统计理论都证明，在大多数情况下，随机误差服从正态分布，如图1-2-1所示.图中横轴为误差△x，纵轴为误差分布概率密度函数f（△x）.可见，遵从正态分布的随机误差具有以下特征：

（1）单峰性.绝对值小的误差出现的概率比绝对值大的误差出现的概率大.

（2）对称性.绝对值相等的正、负误差出现的概率相同.

（3）有界性.在一定的测量条件下，误差的绝对值不超过一定限度.

（4）抵偿性.随机误差的算术平均值随着测量次数的增加而越来越趋向于零.

因此，增加测量次数可以减小随机误差，随机误差是一种具有抵偿性的误差.

著名数学家、物理学家高斯（德国，1777—1855年）于1795年给出了正态分布的函数表达式，

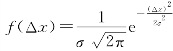(https://www.xing528.com)

式中，△x=x-A，表示每次测量的误差，A为真值，f（△x）是误差△x出现的概率密度，σ为曲线拐点处横坐标值的绝对值，它是表征测量值离散程度的参数，称为正态分布的标准误差.曲线越陡，σ越小，则测量精密度越高，随机误差越小，即反映测量重复性越好；σ越大，则反之，如图1-2-2所示.

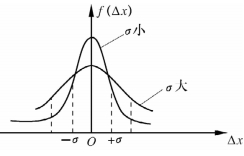
图1-2-2　标准误差的意义

在相同条件下，对某一物理量进行多次测量，称为等精度测量.理论上，通过对被测量无限多次的等精度测量，可得到其真值，即为无限多个测量值的算术平均值.

标准误差σ的数学计算式为

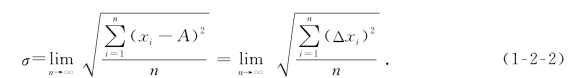
标准误差σ有明确的统计学意义，测量次数n→∞时，被测量的任一次测量值的随机误差落在[-σ，+σ]区间的概率是68.3%，落在[-2σ，+2σ]区间的概率是95.4%，落在[-3σ，+3σ]区间的概率是99.7%.换句话说，任一次测量值落在[A-σ，A+σ]区间的概率是68.3%，落在[A-2σ，A+2σ]区间的概率是95.4%，落在[A-3σ，A+3σ]区间的概率是99.7%.我们把某一数据落在给定区间的概率称为置信概率，用P表示，相应区间称为置信区间.