地震系数法计算与当前静力法计算结果对比分析

本书使用地震系数法方法来计算隧道衬砌地震作用力时对当前的计算方法进行了如下改进：①给出了地震中隧道上方土体计算高度的计算公式，明确了地震中隧道上方土体对隧道衬砌的作用；②研究了地震中围岩对隧道衬砌的作用方式，给出了用于计算衬砌地震力的计算模型。前面通过将地震系数法计算结果与数值计算结果对比验证了其适用性，以下将地震系数法计算结果和使用当前静力计算方法的计算结果进行对比，从而检验本文提出的地震系数法的改进效果。

分析中将本书地震系数法计算结果和使用当前计算方法的计算结果（静力法）分别与使用动力有限元的数值法计算结果进行了比较，见表4-6。

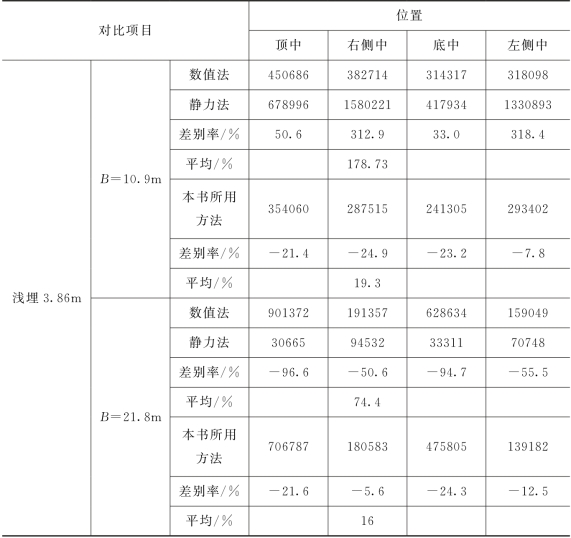
表4-6　　衬砌地震力计算结果对比表（衬砌受到的最大主应力σ1）

续表(www.xing528.com)

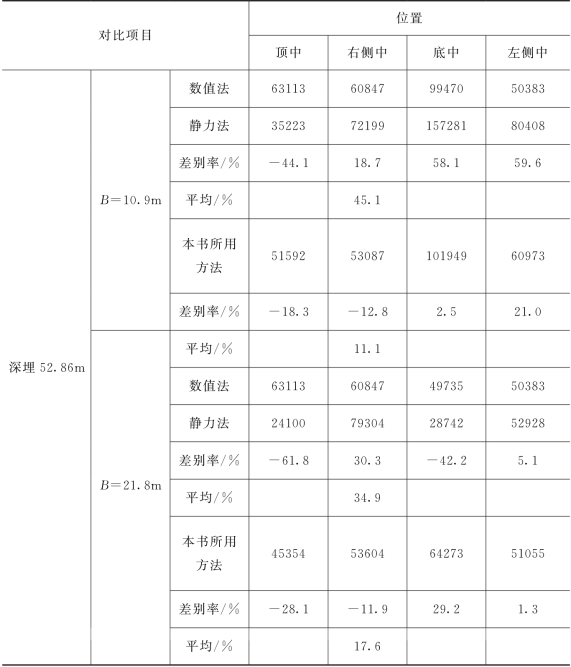
注　表中应力数据的单位为Pa。

表4-6所列数据为最大主应力σ1（Pa），计算采用Ⅱ级围岩，浅埋隧道埋深3.86m，深埋隧道埋深52.86m，计算两个跨度的情况（B=10.9m和B=21.8m）。数值法采用了4.3节给出的计算方法，本书所用方法采用了4.2节给出的地震系数法进行计算，静力法采用了《公路隧道设计细则》（JTG/T D70—2010）中给出的计算方法，表中的差别率是用本书所用方法（或静力法）的数值减去数值法的数值后再除以数值法的数值得到的（“—”号表示该数值小于数值法的数值），表4-6中列出了隧道衬砌上4个位置处的应力值（图4-18），平均值表示衬砌4个位置处差别率绝对值的算术平均值。由表4-6中数据可以看出：①不论衬砌的哪个位置，本书所用方法的计算结果与静力法相比都更接近数值法的计算结果，说明本书所用方法更符合实际情况；②使用静力法计算浅埋隧道时的误差更大（平均差别率为178.73%和74.4%），本书所用方法对深埋、浅埋隧道的计算差别相差不大；③静力法的计算结果受隧道跨度的影响较大，本书所用方法的计算结果受跨度的影响较小。

以上计算结果数据对比分析表明，在计算隧道衬砌地震力时，本书使用的地震系数法（本书所用方法）的精确度更高，更加符合实际。