隧道衬砌地震作用力研究：计算结果分析

分析中选取了衬砌上的特定节点进行对比，如图4-18所示。

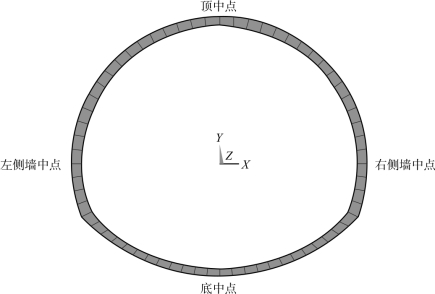
图4-18　隧道衬砌制定对比点位示意图

1.地震系数法计算结果分析

进行隧道衬砌地震力计算时，采用4.2节给出的地震系数法计算模型进行计算，如图4-19所示。图中，q、q′为隧道衬砌顶、底部受到的围岩压力；e1、e2为隧道衬砌两侧受到的围岩压力；Δe1、Δe2为地震作用下，衬砌两侧受到的围岩压力增量；Eh为地震作用产生的衬砌惯性力，分成两半分别作用在左、右侧衬砌上；τ为地震作用下，隧道上方土体对衬砌的作用力。

围岩对衬砌的约束按照径向和切向反力弹簧模型计算，具体荷载的计算如4.2节所述。计算结果均是针对马蹄形隧道、Ⅱ级围岩的情形，围岩参数见表4-5，地震波为水平方向EL波，烈度为8度（峰值加速度0.3g）。

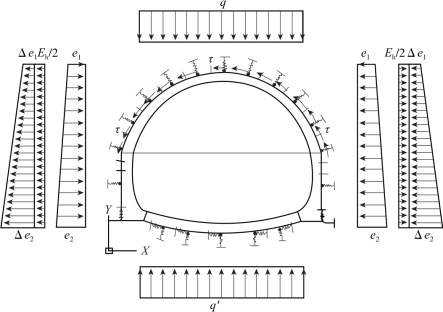
图4-19　地震系数法计算模型

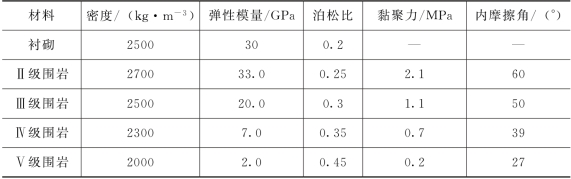
表4-5　围岩参数

计算结果如图4-20所示。

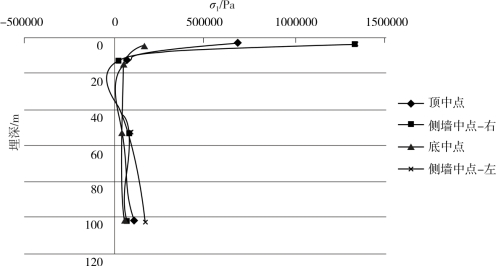
图4-20　地震系数法计算应力随埋深变化图（综合）

由图4-20可知：①隧道衬砌上的最大主应力随着埋深的增加先减小，然后略有增加，最后趋近于一个定值；②当埋深较浅时，隧道衬砌两侧处的最大主应力要大于隧道顶部和底部，隧道衬砌底部的应力最小；③当埋深较大时，隧道衬砌各处的最大主应力相差不大；④隧道衬砌上的应力随埋深的变化存在有明显的转折。

2.数值计算结果分析

数值计算采用4.3节的计算模型（图4-21），模型宽600m，高260m，隧道尺寸为标准公路两车道设计模型。衬砌宽12m，高10.6m，衬砌厚度40cm，采用黏弹性边界条件。按照平面二维平面应变模式计算。围岩参数与地震系数法计算相同，地震波为水平方向EL波，烈度为8度（峰值加速度0.3g）。

图4-21　数值计算模型

数值计算中针对不同隧道埋深、围岩材料、隧道结构形式等多种因素进行了计算，计算结果如下。

（1）不同围岩级别对比（马蹄形隧道），如图4-22～图4-25所示。

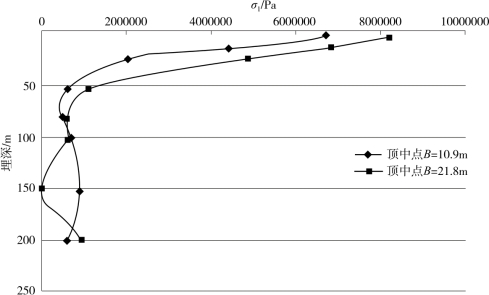
图4-22　不同围岩级别隧道衬砌σ1随埋深变化图（Ⅱ级）

由图4-22可知，对于Ⅱ级围岩：①隧道顶部中点处的最大主应力随着埋深的增加先减小，然后略有增加，基本上趋近于一个定值；②当隧道的跨度较大（B=21.8m）时，隧道顶中点处的最大主应力分布稍有凌乱，但总体趋势与跨度较小（B=10.9m）时一致。

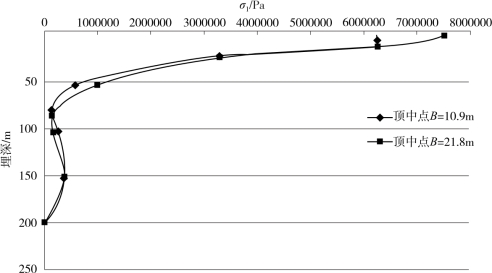
图4-23　不同围岩级别隧道衬砌σ1随埋深变化图（Ⅲ级）

由图4-23可知，对于Ⅲ级围岩：①隧道顶部中点处的最大主应力随着埋深的增加先减小，然后基本上趋近于一个定值；②隧道跨度对衬砌最大主应力的影响很小。(www.xing528.com)

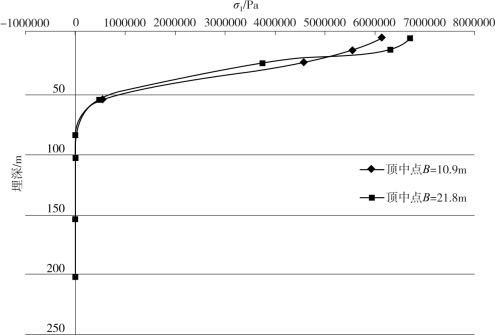
图4-24　不同围岩级别隧道衬砌σ1随埋深变化图（Ⅳ级）

由图4-24可知，对于Ⅳ级围岩：①隧道顶部中点处的最大主应力随着埋深的增加先减小，然后基本上趋近于一个定值；②隧道跨度对衬砌最大主应力的影响很小。

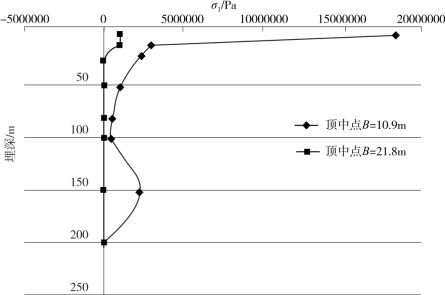
图4-25　不同围岩级别隧道衬砌σ1随埋深变化图（Ⅴ级）

由图4-25可知，对于Ⅴ级围岩：①隧道顶部中点处的最大主应力随着埋深的增加先减小，然后基本上趋近于一个定值；②隧道跨度对衬砌最大主应力有一定的影响。

（2）不同隧道结构形式对比，如图4-26～图4-28所示。

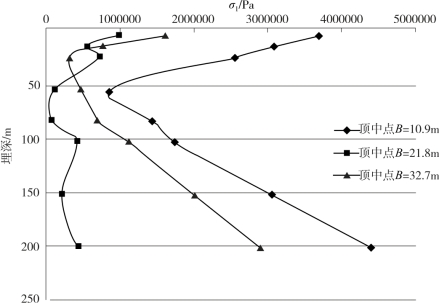
图4-26　不同隧道结构形式衬砌σ1随埋深变化图（矩形）

由图4-26可知，对于Ⅴ级围岩、矩形隧道：①隧道顶部中点处的最大主应力随着埋深的增加先减小，然后又逐渐增大；②隧道跨度对衬砌最大主应力有一定的影响，最大主应力与埋深的变化幅度随着跨度的降低先减小后增大。

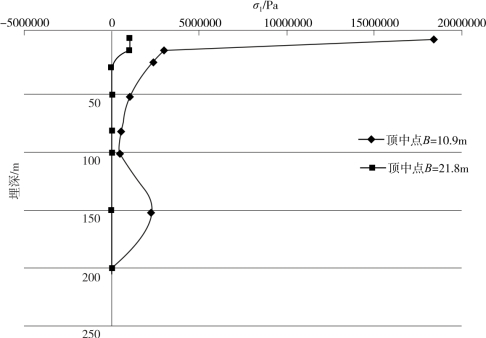
图4-27　不同隧道结构形式衬砌σ1随埋深变化图（马蹄形）

由图4-27可知，对于Ⅴ级围岩、马蹄形隧道：①隧道顶部中点处的最大主应力随着埋深的增加先减小，然后基本上趋近于一个定值；②当埋深较小时，小跨度隧道（B=10.9m）衬砌上的最大主应力要大于大跨度隧道（B=21.8m）。

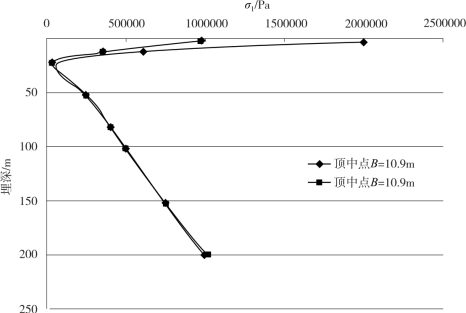
图4-28　不同隧道结构形式衬砌σ1随埋深变化图（圆形）

由图4-28可知，对于Ⅴ级围岩、圆形隧道：①隧道顶部中点处的最大主应力随着埋深的增加先减小，然后又逐渐增大；②隧道跨度对衬砌最大主应力基本没有影响。

由图4-26～图4-28可知：①总体来说，隧道顶部中点处的最大主应力随着埋深的增加先减小，然后又逐渐增大，最后趋近于一个定值；②不同隧道结构形状（矩形、马蹄形和圆形）对隧道衬砌应力的分布有一定的影响，其中矩形隧道的影响最大，圆形隧道的影响最小；③当埋深较大时，隧道衬砌各处的最大主应力相差不大；④隧道衬砌上的应力随埋深的变化存在有明显的转折。

（3）不同地震波作用对比。

分别采用EL波、阪神波和汶川波进行了动力计算分析，结果如图4-29和图4-30所示。

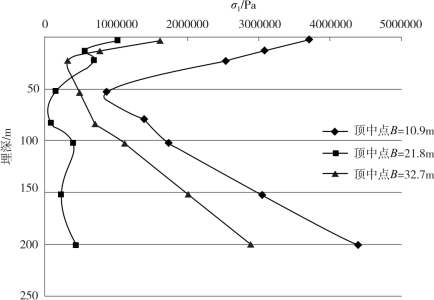
图4-29　不同地震波衬砌σ1随埋深变化图（EL波）

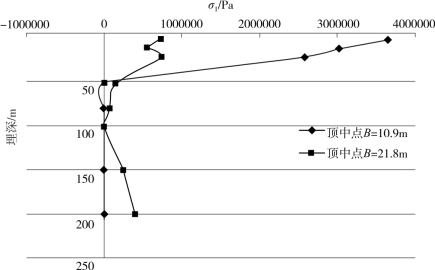
图4-30　不同地震波衬砌σ1随埋深变化图（汶川波）

由图4-29和图4-30可知，当围岩条件较差时（V级）：①不同地震波对隧道衬砌应力分布的影响不大；②EL波作用下，埋深较大时应力有所增加，汶川波作用下，埋深较大时应力趋近于一个定值；③两种地震波作用下，应力随埋深的变化存在有明显的转折。