由前述分析可知,径向和切向反力弹簧模型能够充分体现在地震作用下围岩与隧道衬砌的相互作用,计算结果能够反映实际情况,故可选用为计算深埋、浅埋隧道地震作用力的地震系数法方法计算模型。
使用径向和切向反力弹簧模型分别进行深埋、浅埋隧道地震力计算时模型中的弹簧参数与隧道埋深有关,深埋、浅埋隧道相差较大,应分别计算选取,下面进行分析说明。
土弹簧刚度可采用静力有限元法获得,将隧道部分看作一个空洞,分别在空洞法向及切向施加单位荷载求得周围土的刚度系数。侧向土弹簧刚度的计算方法如图4-8所示,同理可计算出顶板和底板处地层弹簧系数[102]。
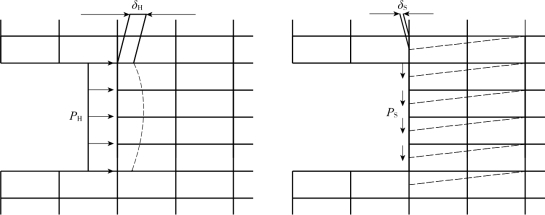
图4-8 土弹簧刚度计算方法
计算公式为

式中 kH——侧墙法向地层弹簧系数;
kS——侧墙切向地层弹簧系数;
PH、PS——单位荷载;
δH、δS——与单位荷载相应的地层变形。
对于曲线形隧道可以通过在隧道衬砌外侧切向和法向施加单位荷载PH、PS,并测出相应的切向和法向变形,采用与矩形隧道相同的方法计算地层弹簧系数,如图4-9所示。
根据上述原理计算出隧道周围围岩的弹性抗力系数如图4-10~图4-12所示。

图4-9 计算中所用隧道周围土层弹簧系数计算图
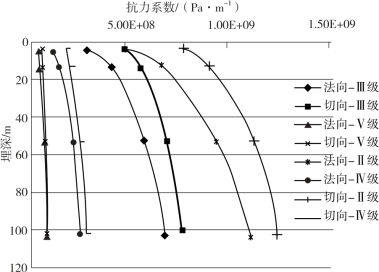
图4-10 围岩抗力系数随埋深变化图(顶部)
由图4-10~图4-12可以看出:
(1)隧道周围围岩的抗力系数在不同埋深处有变化。
(2)在隧道埋深较小(浅埋)时,围岩抗力系数受埋深的影响较大,埋深较大(深埋)时围岩抗力系数受埋深的影响较小,逐渐趋近于一个恒定值。
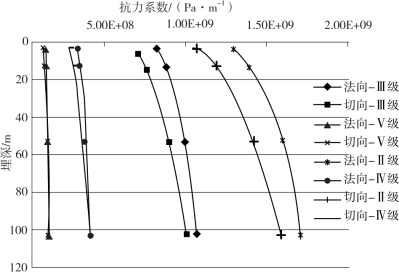
图4-11 围岩抗力系数随埋深变化图(两侧)(https://www.xing528.com)
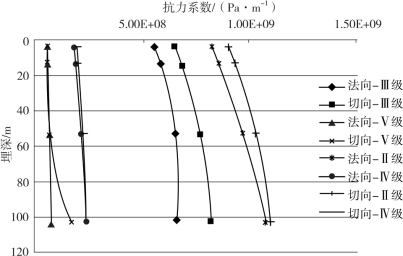
图4-12 围岩抗力系数随埋深变化图(底部)
(3)隧道周围不同位置处(顶部、两侧和底部)围岩的抗力系数不同。
(4)围岩的抗力系数值与围岩的种类有关,围岩的性质越好(Ⅴ级![]() Ⅱ级),其抗力系数值越高。
Ⅱ级),其抗力系数值越高。
(5)使用前述地震系数法计算模型进行计算时,不同埋深、部位的等效土体弹性系数应该采用不同的数值,以便精确模拟计算。
径向和切向反力弹簧模型具有切向和法向两组弹簧,两者的围岩抗力系数不同,为研究其取值规律,这里定义围岩抗力系数切法向比值为:某一位置处围岩的切向抗力系数值与法向抗力系数值之比。下面绘出围岩抗力系数切法向比值随隧道埋深的变化图,如图4-13~图4-15所示。
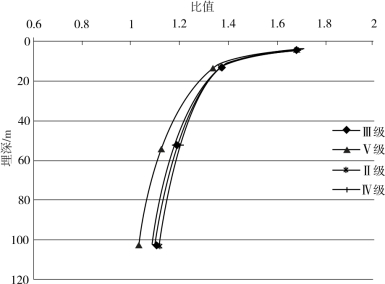
图4-13 围岩抗力系数切法比随埋深变化图(顶部)
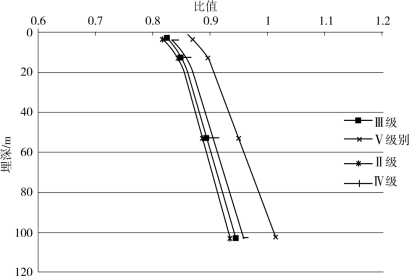
图4-14 围岩抗力系数切法比随埋深变化图(两侧)

图4-15 围岩抗力系数切法比随埋深变化图(底部)
由图4-13~图4-15可以看出:
(1)围岩抗力系数切法向比值在不同埋深处有变化,且在隧道顶部变化较大,隧道底部变化最小。
(2)隧道顶部的围岩抗力系数切法向比值在隧道埋深较小(浅埋)时逐渐减小,变化很剧烈,在隧道埋深较大(深埋)时变化不明显,隧道底部的围岩抗力系数切法向比值受隧道深、浅埋的影响较小。
(3)围岩抗力系数切法向比值受到围岩种类的影响,并且这种影响在隧道底部较大,两侧墙处次之,顶部最小。
由此可见,在选取隧道围岩的抗力系数时,不仅其数值与隧道的深埋、浅埋有关,切向和法向抗力系数的比值也与隧道的深埋、浅埋性质有关。
此外,考虑到围岩在动力状态下的弹性参数与静力状态有所变化,在具体计算中还应根据地震波的强度进行一定的调整,围岩的弹性抗力系数的取值统计见表4-4。具体计算中选取土层弹簧参数时也可以参照表4-4进行。
表4-4 围岩的弹性抗力系数表
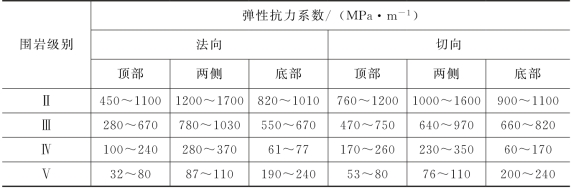
由上面分析可知:在使用地震系数法进行隧道地震力计算时,隧道埋深是影响围岩(土层)弹性抗力系数取值的一个重要因素,浅埋隧道和深埋隧道的取值差别较大,应区别对待。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




