压力拱理论在隧道围岩压力计算中的应用

1.压力拱理论在隧道围岩压力计算中的研究现状

压力拱的研究起源于人类对自然现象的观察和认知，随后根据自然现象进行了理论分析研究，并将理论研究成果应用到具体工程实践中。英国科学家罗伯茨［70］（1884）在对粮仓的受力进行研究时，观察到粮仓底面所承受的力在粮食堆积到一定高度后保持恒定而不再增加，这种粮仓效应后来在土木工程中也被大量发现，称为土拱效应。Terzaghi［71］（1943）通过活动门试验证实了土拱效应的存在，并对土拱效应中的应力分布情况进行了分析研究，进而得到了土拱效应的两个存在条件：①土体之间产生不均匀的相对位移；②形成支撑拱体的拱脚。普罗托奇扬科诺夫［72］（1907）提出了著名的普氏卸荷拱理论，该理论认为拱的拱跨和矢高只与隧道开挖尺寸和隧道周围土的松散体综合摩擦角有关，而与隧道的埋深无关，作用在隧道上的土压力为拱体以下破碎介质的重量所产生的压力。普氏卸荷拱理论能够用来解释在自然界普遍存在的一个力学现象：当隧道埋深较大时，隧道支撑结构上受到的围岩压力与埋深无关。Finn［73］（1963）利用经典弹性理论对土木工程中的土拱效应进行了研究，研究结果表明：土拱效应中往往产生较大的变形，经典弹性理论不再适用。Kellogg［74］（1987）根据对实际工程中拱现象进行观察后发现，土拱具有不同的形状，如抛物线形、半球形、圆弧形等。吴子树等［75］（1995）综合土工离心模型试验结果、实地调查结果和理论分析研究了土木工程中的土拱效应的形成机理及存在条件。尤昌龙［76］（1995）通过对加筋土拱的受力特性进行分析，归纳出了加筋土中的拱形，研究发现加筋土承载能力提高的原因在于加筋土结构具有空间拱效应。贾海莉等［77］（2003）分析了拱脚的存在形式、拱形、拱体几何参数和微观特性等在土木工程领域存在的几个值得探讨的问题。

压力拱的概念是从应力场的角度出发推导出来的［78］，在进行岩土体的开挖施工时，改变了岩土体内部原有的应力传递状态，开挖土体上部的荷载沿着开挖边界线逐渐向两侧和下方传递，在应力的作用下逐渐形成密实的拱体结构，通过拱体结构将开挖土体上部的荷载绕过开挖土体传递到开挖土体下部，形成新的力的平衡体系。

压力拱体是由洞室围岩的不均匀变形形成的，岩土体内发生的不均匀变形致使一定范围内围岩产生相互“楔紧”的作用，从而形成压力拱体。针对压力拱的外边界是封闭型曲线还是一段曲线（即压力拱拱体是否封闭）有不同的研究结论，一些文献认为，压力拱的外边界是封闭型曲线，如图3-1所示。

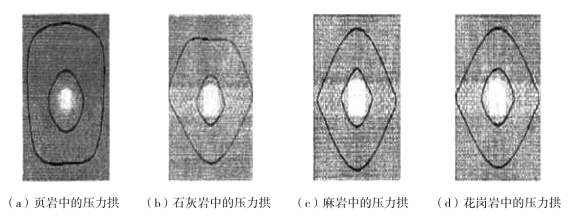
图3-1　弹塑性材料中的压力拱

压力拱在隧道结构中是客观存在的。但在具体判断其形状和内外边界方面还有待统一，当前的主要研究成果有：梁晓丹等［79］研究认为不论围岩破坏与否，最大主应力都在压力拱的内边界上最大，根据这一特点，可判定压力拱的内边界；喻波等［80］研究认为压力拱的外边界是一个封闭曲线；李奎等［78］研究认为压力拱的外边界不一定是一个封闭曲线，需要根据洞室围岩内应变能增大区是否覆盖整个洞室断面以及剪应力临界线是否呈十字形分布来判断压力拱是否为封闭的环状体。对隧道结构周围压力拱的研究主要集中在静力方面，地震振动下隧道周围压力拱方面的研究还较少，本章正是基于此情况研究地震激励下隧道周围压力拱的变化情况，进而确定地震作用下隧道上方土体的计算高度。

2.压力拱理论在隧道地震围岩压力计算中的应用

当前常用的计算压力拱的理论为太沙基理论和普氏理论，但是两者都是针对自重静力状态而言的，地震作用下压力拱确定方面的研究还未见报道，笔者在此做一尝试。

将静力状态下的太沙基压力拱理论引入到地震动力计算中，从而考虑地震作用下隧道上方压力拱的变化情况，计算图示如图3-2所示（假设隧道上方土体沿与竖直成θ的方向破裂）。

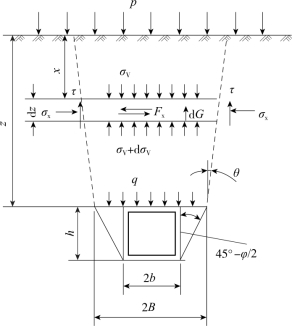
图3-2　地震作用下隧道上方围岩压力计算图示

图3-2中Fx为地震作用下，产生的计算土条地震惯性力，与地震方向一致（向左、右均有可能），p为地面超载，天然地面p=0，2b为隧道跨度，隧道开挖对围岩的影响范围为：从隧道底部呈45°-φ/2的角度向上部扩展，到达隧道顶后，变成以θ角向两侧上方继续扩展（θ角的大小受地震强度和围岩条件的影响），从隧道上部的影响土体中取出dz高的一个土条（土条至地面的距离为z）进行受力分析，σV为土条上方受到的竖向应力，dG为土条的重量，τ为土条两侧受到的剪切力，σx为土条两侧受到的水平向应力，q为隧道顶部位置处的围岩竖向压力。

根据土条的竖向受力平衡可得

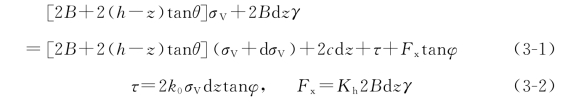
式中　2B dzγ——土条的重量；

　　　γ——隧道上方围岩的容重，计算土条体积使用2B dz进行了近似简化处理；

　　　2c dz——土体间的黏聚力；

　　　τ——土条两侧受到的剪切力；(www.xing528.com)

　　　Fx——水平向地震力，水平地震的方向可能为左，也可能为右，但是在隧道开挖的影响下，隧道上方土体相对其两侧土体有向下位移的趋势，故由水平地震力引起的土条两侧的摩擦力总是向上；

　　　Kh——水平地震系数；

　　　k0——侧向土压力系数。

将式（3-2）代入式（3-1）得

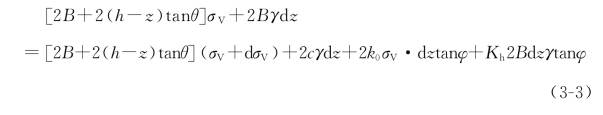
化简式（3-3）得

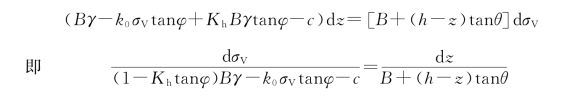
两端积分得

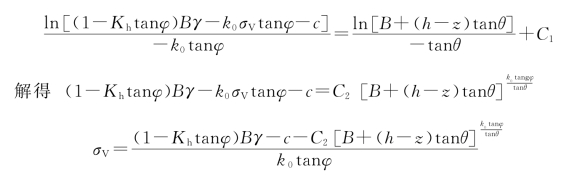
代入初始条件，当z=0时，σV=p。

可以解得

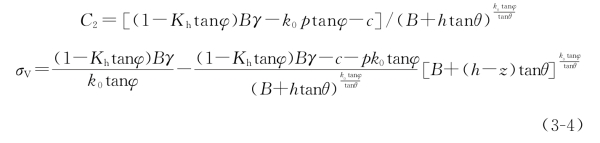
当z=h时，由式（3-4）可以计算出隧道上方的围岩压力为

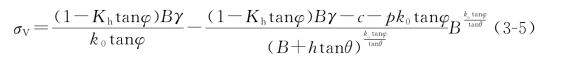
当h→∞时，由式（3-5）可得：σV=B（1-Kh tanφ）γ/（k0 tanφ），即隧道上方的围岩压力趋于一个恒定值。当不受地震作用时，隧道上方的围岩压力的计算公式为σV=Bγ/（k0 tanφ）［81］可见，地震作用引起了隧道上方的围岩压力的变化。

至此，得到地震作用下隧道上方土体计算高度的解析计算公式为

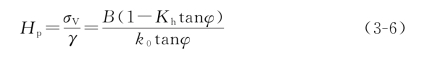
此高度Hp可以看做是在地震作用下隧道上方压力拱的边界高度（说明：在本文中Hp作为地震作用下隧道上方土体的计算高度），即在地震作用前后隧道上方压力拱高度有所变化，但变化得不多，变化数值为BKh/k0，其中，B=b+h tan（45°-φ/2）（说明：此式表示隧道两侧围岩不稳定情况下的计算公式，对于隧道两侧围岩稳定的情况，直接取B=b），b为隧道跨度的一半，h为隧道高度，γ为隧道上方围岩的容重。需要注意的是：式（3-5）和式（3-6）是基于太沙基碎散体理论推导而来的，它们只适用于围岩条件较差的情况（Ⅳ级、Ⅴ级和Ⅵ级围岩），用于Ⅰ级、Ⅱ级和Ⅲ级围岩时需要进行修正。