衬砌结构地震动力分析中的强度折减法应用

在使用数值方法研究隧道结构的破坏情况时，强度折减法是一种常用的方法，近年来，在边坡、隧道与地下结构等岩土工程的稳定性分析中得到了广泛的应用，取得了不错的效果。

1.强度折减法在岩土工程计算分析中的应用现状

有限元强度折减分析方法充分利用了有限元方法和强度折减技术的各自特点，将两者结合在一起，首先对岩土体的强度指标进行折减，然后对折减后的岩土体进行有限元计算分析，再根据某一表征岩土体的应力应变特征的指标（位移、广义剪应变等）作为评判指标，据此基于强度理论和一定的经验评判准则来确定岩土体的极限平衡状态，通过强度折减计算可以将计算过程最后一步所用的强度折减系数作为岩土体材料的安全系数。有限元强度折减法首先应用在边坡的稳定性分析中，近年来，逐渐被引入到隧道和地下工程等一般性岩土工程中来。Griffith等人［56］使用非线性强度折减有限元方法对岩土体材料进行了稳定性分析，得到了比较满意的结果；陈卫兵等［57］提出了采用黏弹塑性模型进行抗剪强度折减有限元计算，并建议用其计算变形结合监测值进行滑坡预警；郑颖人等［58-59］将有限元强度折减法应用于隧道稳定性分析中，并对隧道的静力安全系数进行了分析，得到了隧道结构的静力安全系数；江权等［60］使用有限元强度折减法对地下洞室群进行了整体性计算分析，得到了隧道群的整体安全系数；李树忱等［61］通过具体算例研究了最小安全系数法，该方法可以用于进行隧道围岩结构的稳定性分析；Yang等［62-64］使用有限元强度折减法对浅埋隧道进行了结构稳定性分析，得到了隧道结构的安全系数；程选生等［65］进一步发展了动力有限元强度折减法，该方法首先对水平地震作用下的模型进行模态分析，得到隧道结构的质量阻尼系数和刚度阻尼系数，然后进行静力计算分析，得到模型竖向边界上的水平向支座反力，再将隧道结构自重应力分析结果转化为温度边界条件，通过热分析得到模型各节点的温度，据此来实现在动力分析中考虑重力的影响，最后采用悬臂梁结构动力分析模型，导入热分析获得的模型各节点的温度，同时在竖向边界上施加由静力计算得到的水平向支座反力，通过不断折减围岩塑性区的凝聚力c和内摩擦角φ，直到计算不收敛为止，从而得到隧道围岩结构在地震作用下的动力安全系数。

岩土体的强度为抗剪强度一般表示为

岩土体在所受外荷载增大和自身强度降低的条件下都可以引起破坏和失稳，故可将式（2-1）两端同除以一个大于1的数k（称为折减系数）对岩土体的强度进行折减，即

此外，还要考虑岩土体的抗拉强度σt，得到一组新的强度参数

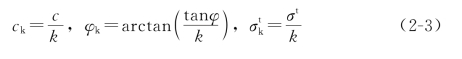
以折减后的抗剪强度参数ck、φk和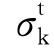为基础建立有限元模型，进行弹塑性有限元数值分析，并逐步判断岩土体是否发生失稳或者达到极限平衡状态。一般从先假定某一个较小的折减系数k开始，逐渐增大k，进行弹塑性有限元计算，直到岩土体达到极限平衡状态，此时所对应的强度参数折减系数k就是岩土体的安全系数，同时根据岩土体的应力应变状态可以判断岩土体的破坏形式。

在有限元法中通过强度折减，根据有限元计算收敛与否来判断结构是否达到破坏，有限元计算不收敛时的折减系数就是安全系数，国外这种方法在20世纪80年代就被采用，但由于力学概念不是十分明确，而且受计算程序及计算精度的影响，这种方法在国内传播较慢［66］。随着计算机技术的发展，尤其是岩土材料的非线性弹塑性有限元计算技术的发展，出现了许多适合于岩土材料的大型通用有限元软件，其前、后处理的功能越来越强大，为利用有限元法进行岩土工程稳定分析创造了条件［66］。

强度折减法在我国最早应用于边坡的稳定分析中，近年来被引入隧道计算中，并取得了很好的效果。隧道结构是和围岩紧密结合在一起的，隧道的破坏表面上是隧道衬砌的破坏，实际上是由围岩的破坏引起的，所以应该充分研究围岩的受力和破坏情况，而强度折减法是研究岩土类材料破坏情况的利器，故使用强度折减法来研究隧道结构的破坏情况越来越引起人们的重视。

动力有限元强度折减法将围岩结构自重转化为节点温度的措施解决了以往动力分析不能考虑结构自重的难题，实现了在动力计算过程中逐渐折减强度的目的，但是，笔者认为还存在如下不足：①通过先将结构自重转化为温度边界条件，通过热分析得到模型各点的温度，再在动力分析中导入热分析获得的各节点的温度来实现自重应力场过于麻烦；②在温度-应力的转换过程中难免存在误差；③进行温度-应力的转换难以考虑隧道开挖过程中应力释放的影响。本书中采用动静力转换边界可以同时满足动力计算和静力计算的要求，在动力计算前施加静力场和静力计算产生的支座反力，首先进行空荷载计算，实现了在地震动力计算中考虑重力的目的，并且计算简便。

2.动力有限元强度折减法基本原理

本书采用的动力有限元强度折减法的计算步骤如下：

（1）建立静、动力计算模型（使用静、动态转换边界）（图2-7）。

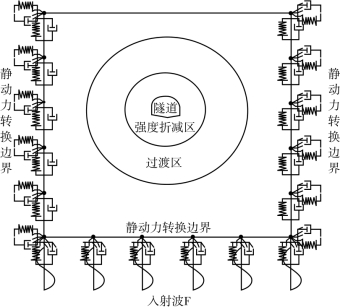
图2-7　动力强度折减法计算模型示意图

（2）使用静力边界，不约束动力边界，进行静力计算。

（3）静力计算得到初始应力场，提取静力边界上的约束反力。

（4）释放静力边界，激活动力边界，将静力边界转换成动力边界。

（5）进行模态分析，得到频率求阻尼。

（6）施加初始应力场（静力），施加前面提取的边界约束反力，进行短时间（0.03s）瞬态体系平衡计算，实现在动力计算分析中考虑重力。

（7）逐步折减强度折减区材料的强度参数，进行瞬态计算分析。

（8）得到隧道结构在地震作用下的破裂面，计算动力安全系数。

动力有限元强度折减法的关键是静动力转换边界，既要保证将隧道开挖施工后形成静应力场施加到瞬态分析中，又要保证合理性和简便性。

动力计算前的自重作用、隧道开挖等静力计算后，隧道结构在重力的作用下形成整个体系（包括隧道、围岩和边界支座反力）力的平衡，整个体系所受的力（相对于后面的动力计算而言称为初始应力）即为重力的影响，在动力计算中不便于施加重力，但可以通过对整个体系（包括隧道、围岩和边界支座节点）施加初始应力场来体现重力的影响。但是，这时计算模型的边界由静力边界变成了动力边界，这就需要进行边界转换，边界转换过程可以由力的传递来推导。

首先明确静力计算和动力计算的具体边界。

静力计算采用两侧简支、限制水平向位移、底部固定的边界条件，如图2-8所示。

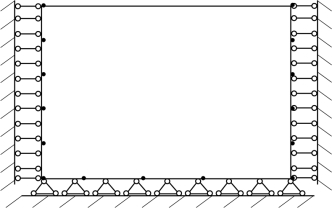
图2-8　静力计算边界图

动力计算的计算模型3侧均采用黏弹边界，如图2-9所示。

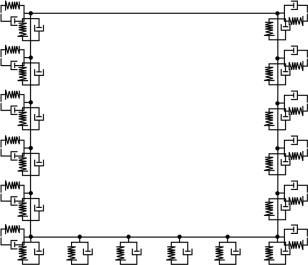
图2-9　动力计算边界图

在静力计算中使用的平衡方程为

式中　K——结构刚度矩阵；(www.xing528.com)

　　　u——位移矩阵；

　　　F——荷载向量矩阵；

　　　FM——静力计算中产生的模型中的等效节点力；

　　　FB——在模型边界处产生的约束反力。

求解式（2-4）即可求出计算模型的静力场为

式中　σ——节点应力矩阵向量；

　　　D——模型弹性矩阵向量；

　　　B——模型几何矩阵向量；

　　　ue——单元节点位移向量。

当以静力场为初始应力条件进行动力计算时，对动力模型施加静力应力场下的荷载和约束是保持模型平衡的先决条件，也是实现在动力计算中考虑重力的必要手段。

将式（2-4）分解成边界内节点和边界节点分开表示，即

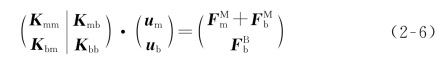
式中　m——计算模型边界以内的自由度；

　　　b——边界上的自由度；

　　　M——外荷载；

　　　B——模型边界上受到的反力。

如果仅考虑内部节点式（2-6）可以表示为

由式（2-6）和式（2-7）可以解得边界节点的约束反力引起的节点荷载向量为

去掉约束条件后，将式（2-7）所表示的约束反力代入式（2-6），可得，ub为0，并且um的解保持不变。

这说明对模型施加约束条件与在边界施加相应的约束反力在静力计算中是等效的，这使得静-动力分析中以静力计算结果为初始应力条件时，可以将约束条件去掉，以相应的约束反力来代替，与原先模型的静力平衡状态保持一致。

承受初始应力场和边界节点反力的隧道结构瞬态分析的微分方程［67］为

式中　M、C、K——质量、阻尼和刚度矩阵向量；

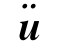　　　（t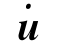）、（t）、u（t）——计算节点的加速度、速度和位移向量；

　　　g（t）——计算模型输入的地震加速度时程；

　　　PM——读入的初始应力荷载；

　　　PB——施加的边界反力荷载。

由以上分析可知，在地下结构静-动力分析中，以静力分析结果中的应力场为初始条件进行动力分析时，为保证模型在动力计算初始时刻为静力平衡状态，可在输入静应力场的同时输入引起此应力场的荷载和约束；转换边界时，须去掉约束条件，只要同时施加以相应的约束反力即可。即通过上述边界转换的方法可以实现在动力计算中考虑重力的影响（施加重力初始应力）。以上方法的准确性可以通过在动力分析中施加零动力荷载来进行检验［68］。

本书使用的动力强度折减法与常规动力强度折减法相比，具有如下特点：①通过静-动态边界的转换在动力计算中考虑重力的影响，常规方法是进行静力计算分析，得到模型竖向边界上的水平向支座反力，然后将隧道结构自重应力分析结构转化为温度边界条件，相比较本书的方法较为简便易用；②在岩土体的折成过程中考虑了抗拉强度的折减，使得计算结果更加符合实际情况；③在进行地震动力计算前进行了短时间瞬态体系平衡计算，便于形成动力平衡体系；④使用的静动力转换边界对计算模型的范围没有特别的要求（一般模型四周尺寸大于4倍洞径即可）。

具体使用动力有限元强度折减法进行计算时，可以采用如图2-10所示的流程进行。

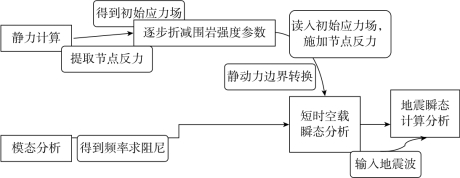
图2-10　本文采用的动力强度折减法计算流程图

本节使用的动力有限元强度折减法通过静动力边界转换、施加初始应力场和边界节点反力等方式实现了在地震动力计算中考虑重力的难题，并且使用静动力边界转换等方式实现了静力计算和动力计算的平稳过渡，保证了动力分析前结构体系的力平衡，通过短时瞬态分析调整从静力向动力转换过程中力场的平衡过渡。整个计算过程简便易行，又保证了体系的稳定，并在随后的计算使用过程中验证了其可行性。