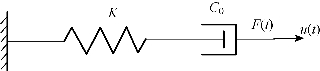
图6-7 混气介质阻尼器力学模型
根据前述分析可知,当阻尼介质中混入气体后,则不能简单地将其视为一种不可压缩流体,这种混气介质已经转变为一种具有黏性和弹性双重特点的液气二相流体。假设混气阻尼介质由黏性流体和弹性固体两部分组合而成,现以黏壶(内充牛顿流体)作为黏性元件,以前述的“液压弹簧”作为弹性元件,将二者串联组成阻尼介质混入空气后的阻尼器力学模型(参见图6-7)。
在这一力学模型中,当受外力作用时,弹性元件的应变是瞬时发生的,其累积弹性变形转变为弹性势能的存储;而黏性元件的应变则随时间持续发展,在产生黏性变形的同时,将外界输入的能量耗散掉。由于黏性元件在模型中串联设置,所以在任何微小外力作用下,整个模型的总变形可以随时间持续发展,与黏滞阻尼器的受力特性相吻合。这一模型即为典型的麦克斯韦模型(Maxwell Model)。
在该串联模型中,总变形为两个元件的变形之和,且两个元件所受的力相等,所以有

且有

式中,ue——弹性元件变形;
uv——黏性元件变形;
Fe——弹性力;
Fv——黏性力;
K——黏滞阻尼器中由于阻尼介质的可压缩性而导致的弹性刚度,可将阻尼介质看作“液压弹簧”,则有K=Ke;
C0——阻尼器的零频率阻尼系数。
令

式中,λ为松弛时间。在通常情况下,如果松弛时间越短,材料的黏性性能越显著;反之,则材料的弹性性能越突出。
由式(6-33)、式(6-34)以及式(6-35)可得(https://www.xing528.com)

因为在该力学模型中,两个元件所受的力相等,故由式(6-36)有
![]()
即采用Maxwell模型作为考虑介质压缩性的阻尼器计算分析模型,其阻尼力以微分方程的形式给出。
对于非线性黏滞阻尼器,例如以高黏度幂律流体作为阻尼介质的细长孔式黏滞阻尼器,根据第3章的相关分析可知,其不考虑阻尼介质压缩性的阻尼力计算公式可简化为
![]()
同理,可以得到考虑介质压缩性后的阻尼力微分方程为

当α=1时,式(6-39)退化为线性Maxwell方程,即式(6-37)。
式(6-37)及式(6-39)可在整体结构的动力分析中与其他结构构件的运动方程同时解出。对设置黏滞阻尼器结构的整体动力分析及减振效果的研究已经有较多成果[4-13],因篇幅原因,这里不再进行具体分析。
式(6-37)及式(6-39)可用于分析黏滞阻尼器考虑弹性变形后对整体结构减振效果的影响,但是对于体现阻尼器本身性能发生的变化不够直观。将式(6-36)进行变换后,可以得到

上式即为以牛顿流体为阻尼介质的阻尼器,由于工作介质中混入气体而需考虑压缩性影响时的阻尼力计算公式。
同理,对非线性黏滞阻尼器有

由式(6-40)和式(6-41)可以看出,由于阻尼介质混入气体后,引起液流体积弹性模量的减小,阻尼器在外界激励下产生的总位移中,有一部分为阻尼介质的累积弹性变形,降低了黏滞阻尼器的耗能能力(弹性变形只能储存能量而不能耗散能量)。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




