液体受压力增大的作用相应使体积缩小的性质称为液体的可压缩性。假设容器中液体初始的压强为p0,体积为V0,当液体压力增大时,其体积缩小,如果液体的可压缩性用压缩系数k表示,则有

式(6-20)指液体因单位压力变化所引起的体积相对变化量,由于压力增大时液体的体积减小,为使压缩系数k为正值,故在上式右侧加负号。
液体压缩系数k的倒数,称为液体的体积弹性模量(用K表示),则有

式(6-21)表示液体产生单位体积相对变化量所需的压力增量。
根据硅油在不同压强作用下的体积变化率[1],经过换算,可以拟合出不同黏度硅油的体积弹性模量随外界作用压强的变化规律(参见图6-3)。由图可知,1000号~12500号硅油的体积弹性模量随压强的增加而线性增大,且拟合函数基本相同。在一个标准大气压作用下,硅油的体积弹性模量大致可取为1.3×104MPa,而钢材的弹性模量一般约为2.0×105MPa,故所配置的硅油基阻尼介质的可压缩性大约为钢材的15倍。
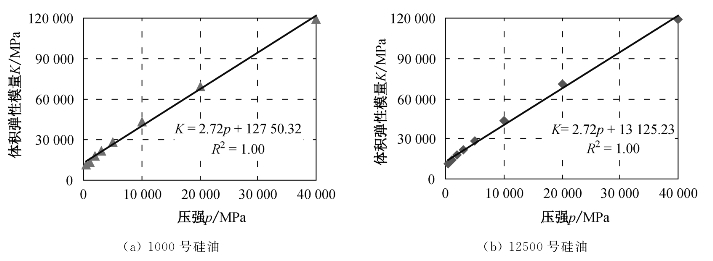
图6-3 硅油体积模量与压强关系曲线
以第3章介绍的细长孔式黏滞阻尼器为例,导杆受力段长400 mm,直径90 mm,如果阻尼器最大输出阻尼力为570 k N,则可以推算出导杆的最大弹性变形约在0.14 mm左右。所以阻尼器在工作时,钢质导杆的弹性变形可以忽略不计。同理,阻尼器的缸筒、活塞等其他钢质零配件的弹性变形也相对较小,可以基本忽略不计。
根据阻尼器的构造尺寸可以推算出,当最大输出阻尼力为570 k N时,阻尼器内部产生的压强约为30 MPa(常规的黏滞阻尼器工作压强一般处于30 MPa以下)。在30 MPa压强的作用下,缸筒内阻尼介质的体积相对变化量约为
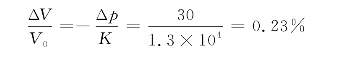
此时,受压阻尼介质将沿活塞运动的方向产生大约0.3 mm的弹性变形。因此,通常在分析黏滞阻尼器的力学性能时,大多假定阻尼介质为不可压缩流体,忽略阻尼介质以及导杆弹性变形对阻尼器性能的影响。
当阻尼介质中混有不溶解的空气时(溶解于油液中的空气,对油液的物理性能基本不产生直接的影响[2]),掺混气体通常以微气泡的形态均匀分布于油液中,由于空气的压缩性很大,将会导致混气油液的抗压缩性显著降低。因此,在分析阻尼介质的可压缩性时,必须综合考虑阻尼介质本身的可压缩性,以及混于其中的空气的可压缩性。
假定体积为Vm的混气油液中,纯阻尼介质的体积为Vo,气体的体积为Vg,当压强增加时,混气油液的体积减小ΔVm,应为纯阻尼介质的体积减小ΔVo及气体的体积减小ΔVg的总和,即
![]()
根据流体体积弹性模量的定义有(https://www.xing528.com)

将式(6-23)~式(6-25)代入式(6-22),得到

将式(6-26)整理后得到
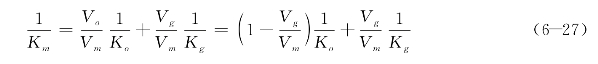
根据式(6-27)可知,如果在一个大气压强(0.1 MPa)的作用下,阻尼介质中混入0.5%的气体,其体积弹性模量将下降为原来的0.15%;如果混有1%的气体,则混气介质的体积弹性模量降低到纯阻尼介质的0.08%。
以上为在一定压强作用下,油液中混入气体后对其体积弹性模量的影响。如果在大气压强作用下,混入油液的气体体积为Vga,原纯油液的体积为Voa,则在压强p作用下混气油液的体积弹性模量Km为[3]
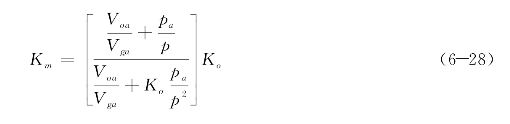
假定在一个标准大气压的作用下,阻尼介质中分别混入了0.5%、1%、5%和10%的空气,则根据式(6-28),可以得到混气阻尼介质的压强逐步增加到1 MPa、10 MPa、20 MPa、30 MPa时,相应的混气介质体积弹性模量以及与纯阻尼介质体积模量的百分比(见表6-1所示)。
表6-1 混入气体对阻尼介质体积弹性模量的影响
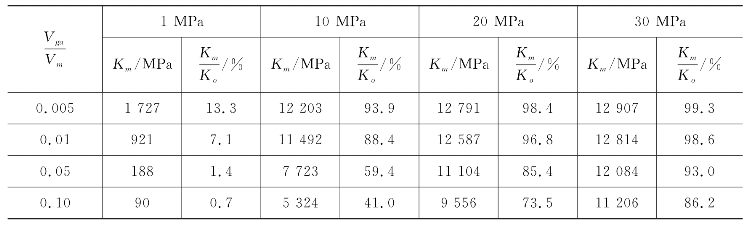
图6-4表达了混入不同比例气体的阻尼介质的体积弹性模量随外界作用压强大小而变化的规律曲线。由图可以直观地看出,在阻尼介质中混入气体体积的多少以及外界作用压强的大小,都会对混气阻尼介质的体积弹性模量产生很大的影响。混入气体越多,阻尼介质的体积模量损失越大,即可压缩性越大;作用的压强越高,体积模量恢复得越多。如果阻尼介质中混气量越少,随外界压强的增大,其体积弹性模量恢复得也越快。

图6-4 混气介质Km—p规律曲线
由上述分析可知,混入空气后阻尼介质的体积弹性模量将被大幅削减,随着所受压力的增加,混气阻尼介质的体积模量得到一定程度的提高,最终接近于纯阻尼介质的体积模量。但是,由于混气介质在初始状态的体积模量非常小,在混气阻尼介质升压的过程中,累积的弹性变形较大。而且,阻尼介质在生产、运输以及在黏滞阻尼器的装配过程中将不可避免地混入一定量的气体,所以在分析黏滞阻尼器的动态性能时,需考虑阻尼介质可压缩性(弹性变形)所造成的影响。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




