工程结构黏滞阻尼器计算公式及应用

根据前述的分析方法，结合本章设计的螺旋孔式黏滞阻尼器的构造参数，经过计算可知，螺旋管道中的二次流动为单涡旋结构，在轴向流动和二次流动的共同作用下，整体流动沿管道轴线方向呈螺旋状前进。因此，黏滞流体在螺旋管道流动过程中的阻力损失主要表现为流体沿螺旋线前进时的沿程阻力损失。

根据文献[37]的推导可知，流体流经平直圆管的压力损失Δp为

式中，l——管道长度；

d——管道直径；

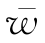——管道轴向平均流速；

ε——管壁粗糙尺度。

所以对于平直管道，其沿程阻力损失可以表述为

式中，λ为摩阻系数，令，反映管道中流体的流态以及管壁粗糙对管壁处的切应力的影响。

圆管壁面对黏滞流体产生的摩擦阻力，可以用管壁处的切应力乘以管壁面积表示。假定管壁处的轴向切应力为τ0，则摩擦阻力Rf=τ0χl，这里χ为湿周。

该摩擦阻力与管道进出口断面的压力F1、F2相平衡，所以有

也即

由式（4-25）、式（4-28）可得

式中，λ1——管内流体轴向运动时的摩阻系数。

同理，可以得到管壁的周向切应力τω为

式中，λ2——管内流体周向运动时的摩阻系数；

——管内流体周向流动的平均速度。

根据能量守恒原理，阻力做功的功率应等于流体功率的损失值，所以有

这里，A=2πRl，，代入式（4-31）得到

整理后得到

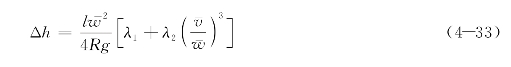
令，d=2R，

所以式（4-33）又可表述为

这里，λ可以看作是螺旋管道内流体流动的摩阻系数，其值大小与雷诺数Re、管壁相对粗糙度以及流体周向与轴向运动速度的相对值有关，其中反映了流体由于在螺旋管道中运动，产生二次流动（周向运动）所引起的摩阻损失。

所以，螺旋管道内流体流动的摩阻系数λ也可以表述为

这样，就得到了黏滞流体在螺旋管道中流动时，其轴向流动和周向流动产生的沿程阻力损失Ef。此外，由前述分析可知，由于螺旋管道二次流的存在，部分流体机械能将转化为出口断面的旋转动能Eω，从而引起压能损失。

为分析简便起见，假定圆截面螺旋通道内因二次流动产生的周向流速沿径向近似呈线性分布，即周向流动（单涡旋）是以断面中心为圆心，以相同的角速度ω进行的旋转运动，所以周向流体的速度分布可以表示为

则管壁处的流速为vR=ωR。

通道断面的平均旋转动能Eω为

因为螺旋通道中，流体的轴向平均速度为，切向平均速度为，可得流速的偏转角度为，所以。

因此，式（4-37）可写为(www.xing528.com)

综合式（4-24）、式（4-34）和式（4-38）可得

若螺旋通道的轴向长度（活塞宽度）为L，螺距为2πk，则有代入式（4-39）并整理可得

通过以上推导，得到了螺旋管道内黏滞流体考虑摩阻损失和旋转动能的影响后，压降Δp与轴向平均流速之间的关系。

设阻尼器缸筒内径、活塞外径均为D1，导杆直径为D2。又因为

故得到阻尼力F与轴向平均流速之间的关系为：

式（4-43）建立了阻尼力F与阻尼介质流经阻尼孔平均流速之间的关系，为便于设计，需要掌握阻尼力F与活塞相对运动速度V之间的变化规律。

现假设活塞上开有n组孔径为d的阻尼圆孔（为方便设计和制造，阻尼孔的直径通常为同一尺寸），流经活塞上各阻尼孔的流体连续性方程为

由式（4-43）、式（4-44）可得

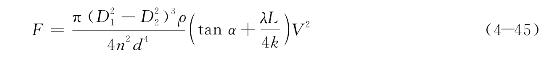
式（4-45）即为螺旋孔式黏滞阻尼器的阻尼力F与速度V的理论计算公式。

需要说明的是，上式并不是说阻尼力F与活塞相对运动速度V之间成2次方关系，因为在式（4-45）中，还有一些跟螺旋管道内流体流态相关的参数tanα、λ，它们的取值受流体的轴向和二次流动周向速度分布形式等因素的影响，进而影响到与活塞运动速度之间的关系。

以上内容借助了众多流体力学的基本理论，介绍了流体在螺旋管道内的流动特点。在此基础上，推导出螺旋孔式阻尼器的阻尼力计算公式。该公式在推导过程中，很多推导步骤都具有相应的前提条件，而且为推导和表述方便，对螺旋管内的流体流动特性参数也做了一定的简化。但是，由于螺旋管内流体流动的复杂性，为了尽量包含螺旋管道流动的特性，得到的阻尼器F—V计算公式仍然不直观，且不便于工程的应用。因此，需要对其进一步进行简化。

现假定螺旋管道中液体速度方向均沿轴线方向，且速度值相等；此外，螺旋管道水力直径小于螺旋曲率直径，故可将螺旋管道上任一微小弧段视为直线流道。

对于牛顿流体圆截面螺旋管道流，其在微小弧段上的压降为

式中，μ——牛顿流体动力黏度。

因为

式中，R——螺旋管中心线曲率半径（参见图4-2）。

将式（4-47）代入式（4-46），沿螺旋管道积分并整理后，可得螺旋管道上流体压降与平均流速的关系为

式中，H——螺旋管的螺距（参见图4-2）。

设阻尼器缸筒内径、活塞外径均为D1，导杆直径为D2。根据式（4-42），得到以牛顿流体为阻尼介质的螺旋孔式黏滞阻尼力理论计算公式为

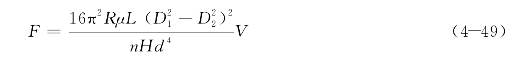
对于采用幂律流体作为阻尼介质的黏滞阻尼器，同理可得圆截面螺旋管道流在微小弧段上的压降为

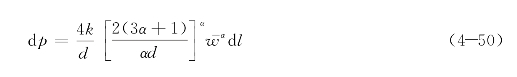
式中，k——稠度系数；

α——流动指数。

将式（4-50）沿螺旋管道积分并整理后，可得

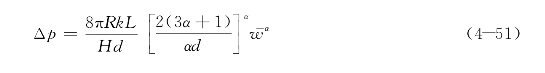
最后得到以幂律流体为阻尼介质的螺旋孔式黏滞阻尼力理论计算公式为

通过式（4-24）可知，黏滞流体在流经螺旋管道后，其压能的损失主要由两部分构成：一部分为流体的沿程阻力损失Ef，另外一部分由于螺旋管道二次流动的存在，部分压能转化为出口断面的旋转动能Eω。式（4-49）及式（4-52）在推导过程中，为简化公式和应用方便，未考虑二次流动引起的损失，且上述公式还需通过阻尼器性能试验对其进行修正。