正交螺旋坐标系构建原理及应用

对物理问题进行计算分析时，选择的坐标系应该具有坐标轴与计算区域的边界相适应的特性。流体运动的边界是各式各样的，对不同的流体力学问题，其内在规律不依赖于所选择的坐标系，但是根据不同的情况选择合适的坐标系，可以更好地满足边界条件，并能有效简化计算过程和提高数值结果精度。

根据在空间任意一点上三个坐标面是否相互垂直，可以将坐标系分为正交坐标系和非正交坐标系两大类。由于能用解析形式表示的坐标系种类有限，为适应实际工程中各种计算区域形状的不同需要，近几年应用数值方法生成适体坐标系的技术得到很大发展[23-26]。

根据螺旋管道的特点（见图4-2所示），可以构建出正交螺旋坐标系（见图4-3所示），以便给出适于求解螺旋管道流体流动的基本方程[27][28]。

假定螺旋管的螺距为H=2kπ，k为常数。

若螺旋管管道半径为r，螺旋管中心线曲率半径为R，则曲率κ和挠率τ可表示为[29]

以{x，y，z}为笛卡儿直角坐标系（见图4-3），

图4-2　圆截面螺旋管道

图4-3　正交螺旋坐标系

则螺旋管道中心线c的参数方程为：

式中s为中心线c的弧长，设c为三阶可微的有向正则空间曲线，取s增加的方向为正方向，则曲线c上任一点M（x0（s），y0（s），z0（s））处的切向矢量为：

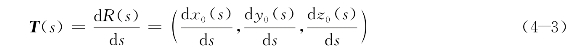
令

则N（s）为中心线c在M点的主法向矢量。

定义矢量B（s）为(www.xing528.com)

称B（s）为中心线c在M点的副法向矢量。

因此，矢量簇（T（s），N（s），B（s））可以构成一个右手正交标架[30]。

在（N，B）平面内建立极坐标（r，θ），固定于螺旋管道中心线c上，建立螺旋坐标系（r，θ，s），如图4-3所示。根据Germano[7]关于螺旋坐标正交化结构的方法，保留切向矢量T（s），将N（s）和B（s）同时绕T（s）旋转某一角度（φ（s）+φ0），φ（s）取下面的形式：

其中φ0和s0取任意值。

则螺旋管中任意一点位置矢量为

故有

由式（4-6）定义，φ0和s0可以取任意值，现取φ0=π/2，则根据式（4-8）可得旋转后螺旋坐标系的协变度量张量为

式中M为

由式（4-9）可知，旋转后的螺旋坐标系满足正交条件（gij=0（i≠j）），为一正交坐标系。该正交坐标系的局部标架为[28]：

在正交螺旋坐标系（r，θ*，s）中，θ*=θ+φ，下文为表述的方便，略去θ上标*，以θ代表θ*。