工程结构黏滞消能减振技术试验结果与分析

1）阻尼介质黏度对阻尼器性能的影响

图3-6　阻尼介质黏度对阻尼器性能的影响

通过试验得到的阻尼力—位移滞回曲线为一个类似于椭圆的曲线，曲线平滑、稳定、饱满，附加刚度很小，基本对称于坐标轴。对于阻尼器S1～S5（阻尼介质为硅油基黏滞材料-1），其滞回曲线形状接近于椭圆，而阻尼器S6（阻尼介质为硅油基黏滞材料-2）和S7（阻尼介质为硅油基黏滞材料-3），滞回曲线形状介于椭圆和矩形之间。在相同工况条件下，后者滞回曲线包围的面积更大，耗能能力相对来说更强，如图3-6所示。图3-6表示在频率为0.25 Hz，幅值为±20 mm的正弦波加载条件下，阻尼器S3、S6、S7的阻尼力—位移滞回关系曲线。

为掌握阻尼介质黏度对阻尼器性能产生影响的本质，对不同黏度的阻尼介质进行了本构关系试验，即利用旋转黏度计测定流体的表观黏度与剪切速率的关系以及剪切应力与剪切速率的关系。

根据试验的结果可知，在较小的剪切速率作用下，高黏度的流体相对于低黏度的流体能产生更大的剪切应力。由图3-6可以看出，在相同加载条件下，阻尼器S7相比S6、S3产生更大的阻尼力。

根据试验可知，对于硅油基黏滞材料-1，其剪切应力与剪切速率基本为线性关系，可以判定其为牛顿流体；对其余阻尼介质，根据其表观黏度与剪切速率的关系，可以判定为非牛顿流体。故黏度的变化导致流体本构关系不同，这也是造成构造相同但采用不同黏度阻尼介质的阻尼器输出力—位移关系曲线形状有差异的根本原因。

2）活塞运动速度对阻尼器性能的影响

根据本章3.3节的分析可知，由于阻尼器的构造和采用阻尼介质的不同，使得阻尼器的计算公式各不相同，但黏滞阻尼器为一种速度相关型阻尼器这一点是共同的，活塞运动速度是影响输出阻尼力大小的主要因素之一。

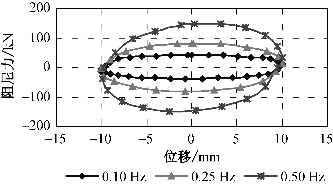
图3-7　活塞运动速度对阻尼器性能的影响

通过阻尼器力学性能试验可以看出，在同一温度和加载频率下，随着输入位移幅值的增加，滞回环所包围的面积逐渐增大，耗能能力也随输入位移幅值的增大而增强。与此类似，在同一温度和控制位移下，随着加载频率的增大，滞回曲线逐渐趋于饱满，阻尼力随加载频率的增大而增大，耗能能力也随加载频率的增大而增强（如图3-7所示）。图3-7为阻尼器S3在正弦波加载，位移幅值为±10 mm，加载频率分别为0.1 Hz、0.25 Hz、0.5 Hz时的阻尼力—位移关系曲线。

试验时在相同的输入波形（比如均为正弦波）控制下，加载频率相同改变控制位移幅值，或控制位移幅值相同调整加载频率，或两者均发生变化，其本质就是使阻尼器活塞的相对运动速度产生变动，从而研究阻尼器在活塞不同运动速度时的力学性能。

从试验结果和理论分析都可以发现，阻尼器输出阻尼力的大小并不独立地受加载频率和位移幅值的影响，其输出力在根本上是与活塞的最大运动速度相关。同一阻尼器在受到外界激励后，无论运动频率和幅值是多少，只要活塞的最大相对运动速度相同，其输出的阻尼力就相同（参见图3-8）。

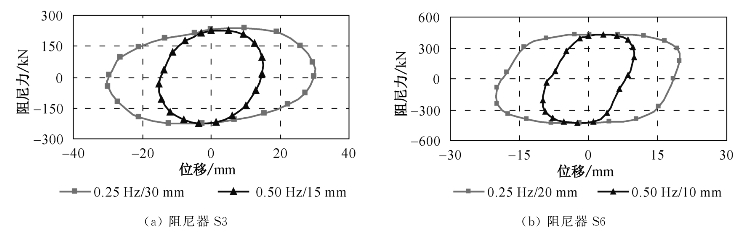
图3-8　最大加载速度相同时阻尼器滞回曲线

为了研究阻尼力F与活塞相对运动速度V的变化规律，通过在试验中采集的不同阻尼器在不同工况下的阻尼力、位移以及采样时间之间对应的数据，经数学处理可得到相应的阻尼力关于速度的滞回曲线（参见图3-9）。

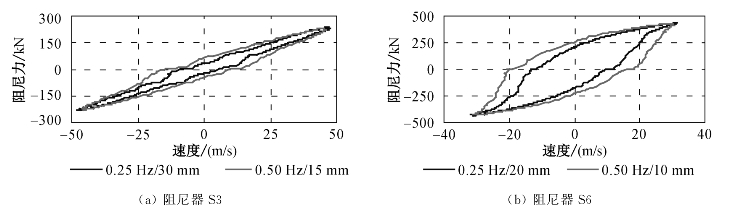
图3-9　阻尼器F—V关系曲线

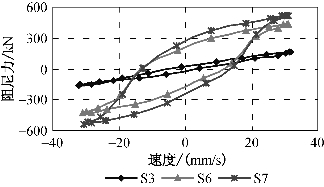
图3-10　相同试验工况下F—V曲线

由图3-9可以看出，不同阻尼器的阻尼力—速度关系曲线形状并不相同。以上试验工况均为正弦波加载，阻尼器S3与S6在构造上完全一样，两者只有阻尼介质的黏度不同。根据前文所述，当阻尼介质黏度增加到一定程度以后，将会由牛顿流体转变为非牛顿流体，所以造成S3与S6、S7的F—V关系曲线形状不同。这一现象通过图3-10的对比后尤为明显。

从图3-9还可以看到，同一阻尼器在最大加载速度相同但加载频率和幅值不同的工况下，F—V关系曲线却并不完全重合，一般加载频率大的工况，F—V曲线包围的面积也相对较大。此外，由图3-10还可得知，不同阻尼器在同一个工况（频率0.25 Hz、幅值±20 mm、正弦波加载）的往复运动过程中各自的F—V关系曲线并不重叠为一条线，且在活塞运动速度为0时，阻尼器输出力并不为0。

将阻尼器S3与S6在频率f=0.25 Hz、幅值为u0=±20 mm及正弦波加载条件下一个周期内阻尼器位移、速度与阻尼力在时域展开，如图3-11所示。对于正弦波加载工况，位移时程方程为u=u0sin（ωt），则相应速度变化为v=u0ωcos（ωt），式中ω=2πf。在时间为1/4周期，即1 s（或3/4周期，即3 s）时，位移达到最大（最小）点，此时速度为0，但相应的输出阻尼力并不为0，此时输出阻尼力的大小与阻尼介质的黏度有关。当阻尼介质黏度较低时（如阻尼器S3），对应速度0点的阻尼力接近于0，速度与阻尼力的相位差很小，二者的变化基本同步；而黏度较高的阻尼器（如阻尼器S6），速度和阻尼力均超前于位移的变化，但是速度与阻尼力的变化并不同步，阻尼力在相位上落后于速度，故在速度为0点时阻尼力尚未衰减到0，阻尼力仍较大而不能忽略。

图3-11　阻尼器位移、速度、阻尼力—时间关系曲线

将阻尼器S6分别在f=0.25 Hz、u0=±20 mm及f=0.50 Hz、u0=±10 mm的控制条件下进行正弦波加载，取2 s内（分别对应半个周期和一个周期）阻尼器速度与阻尼力的时程曲线（如图3-12所示）。通过对比可以看到，这两个工况加载频率和幅值不同，但是最大速度一样。当其加载速度达到最大时，两个工况均达到最大输出阻尼力，且大小相等。当加载速度为0时，两个工况的阻尼力均不为0，加载频率高的工况，速度0点的阻尼力相对较高。由此可见，加载速度0点对应的输出阻尼力不仅与阻尼器采用介质的黏度有关，还与阻尼器的工作激励条件相关。

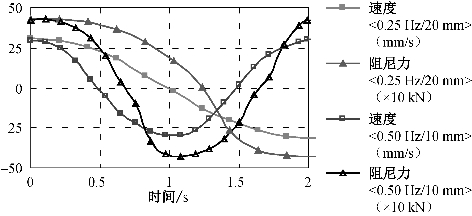
图3-12　阻尼器速度、阻尼力时程曲线

图3-11、图3-12表达的是阻尼器在外界激励下往复运动的过程中所表现出的基本性能，当阻尼器在遭遇外界激励的开始以及停止时段，其位移、速度与阻尼力的关系略有不同。图3-13为阻尼器S3在f=0.5 Hz、u0=±20 mm、f=1.0 Hz、u0=±10 mm及正弦波加载条件下起始阶段各参数随时间的变化情况。通过图3-13可知，在初始阶段，阻尼器反馈的速度、阻尼力均随外界输入位移由0开始变化。速度与阻尼力的变化基本同步进行，但其变化周期较位移变换的周期短，在一个位移加载周期内，速度与阻尼力的变换约已完成5/4个周期，从而使得阻尼器在第2个位移加载周期开始时，速度与阻尼力在相位上已较位移超前1/4个周期，其后的位移、速度和阻尼力变化规律如图3-11、图3-12所示。

图3-13　运动起始段位移、速度、阻尼力时程曲线

图3-14为阻尼器S3在f=0.5 Hz、u0=±20 mm、f=1.0 Hz、u0=±10 mm及正弦波加载条件下停止阶段各参数随时间的变化情况。由图3-14可以看出，在控制位移的最后一个周期内，随着输入位移幅值的减少，速度和阻尼力的相位再次逐步超前，并且在输入位移停止在初始位置时，又提前1/4个周期，速度和力也同时衰减为0。在最后一个循环前的位移、速度和阻尼力变化规律仍然如图3-11、图3-12所示。经过整个循环加载过程后，速度和阻尼力的变化相位累计超前位移变化1/（2f）的相位。

图3-14　运动停止段位移、速度、阻尼力时程曲线

当阻尼介质黏度比较高时，位移、速度、阻尼力在运动起始段和运动停止段的变化规律与低黏度阻尼介质时的情况基本一样，只是阻尼力的相位介于速度和位移之间，而低黏度阻尼介质速度与阻尼力基本同步变化。

3）阻尼孔径对阻尼器性能的影响

通过本章的阻尼器耗能机理分析可知，阻尼孔径的大小也是影响阻尼器性能的一个重要参数之一。阻尼孔径确定后，实际决定了活塞上阻尼孔流通面积的大小，进而影响到阻尼器在工作时，阻尼介质在流经阻尼孔时的流动形态参数，包括流量、平均流速、流速分布形式等，并最终影响阻尼器的滞回曲线形态及最大输出阻尼力等性能参数。

通过试验可以看到，保持输入位移幅值、激励频率和阻尼介质不变，随着阻尼孔增大，最大阻尼力减小，滞回环逐渐趋于扁平，耗能能力降低；反之，随着阻尼孔的减小，最大阻尼力增大，滞回环逐渐趋于饱满，耗能能力也随之增大。图3-15为阻尼器S1～S5在f=0.5 Hz、u0=±15 mm正弦波加载条件下的阻尼力—位移滞回关系曲线。阻尼器S1～S5除阻尼孔径不同外，其余构造以及阻尼介质均相同。由图中可以看到，随着阻尼孔径的减小，不仅滞回曲线更加趋于饱满，而且形状也发生一定程度的变化。(www.xing528.com)

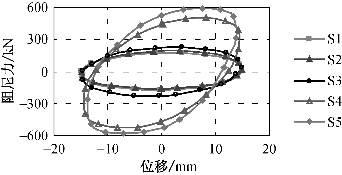
图3-15　阻尼孔径对性能的影响

从参与试验对比的阻尼器来看，当阻尼孔径大于或等于2.4 mm时，阻尼力—位移滞回曲线基本对称于坐标轴；当阻尼孔径进一步减小时，滞回环出现了一定程度的倾斜，表明此时阻尼器已具有一定的刚度。

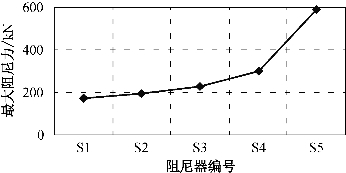
图3-16　阻尼孔径对最大阻尼力的影响

经过分析后认为，当活塞进行往复运动时，如果活塞上的阻尼孔过小，则有可能阻尼介质在活塞两端压差作用下不能及时从高压区域通过阻尼孔流到低压区域，而活塞的运动幅度又必须与外界激励相谐调，故压缩阻尼介质产生一定的弹性变形，也包括活塞导杆在外力作用下自身产生的弹性变形，最终导致阻尼器出现瞬时刚度。

图3-16为阻尼器S1～S5在f=0.5 Hz、u0=±15 mm正弦波加载条件下的最大阻尼力变化趋势。从图中可以看出，在最大加载速度相同的情况下，随着阻尼孔的逐步减小，相应的最大阻尼力依次递增。

以上只是定性分析，为了更准确地把握最大阻尼力与阻尼孔径的关系，研究了在同一工况下，最大阻尼力之比与阻尼孔面积之比间的相互关系（参见图3-17）。在图3-17（a）中，给出了四条曲线，分别是阻尼孔面积比曲线，对应最大阻尼力比曲线，以两者各自的关系拟合曲线及拟合公式。由图3-17（a）可以看到，对于阻尼器S1～S5，其阻尼孔面积比曲线大致呈一水平线，其曲线拟合公式中，二次项和一次项的系数均很小，可近似为一常数。而最大阻尼力之比曲线的拟合公式则是一非线性方程。通过图3-17（b）可见，最大阻尼力之比与阻尼孔面积比之间关系的拟合曲线，采用二阶多项式的拟合精度要高于线性拟合，故最大阻尼力的增加与阻尼孔截面面积的减小并不成正比关系，也即这两个参数不是线性相关。

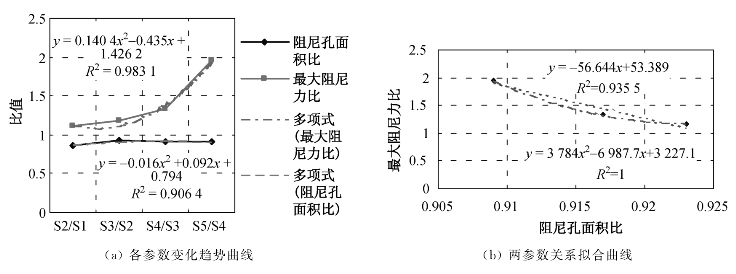
图3-17　阻尼孔径与最大阻尼力关系

4）阻尼孔长对阻尼器性能的影响

流体力学中规定[1-3]，在直径为D的通道中，假设阻尼孔的直径为d，长度为l，当0＜l/d≤0.5时，该孔为薄壁小孔；当0.5＜l/d≤4时，为厚壁小孔或短孔；当l/d＞4时，为细长小孔。阻尼孔长径比的变化，会导致流体通过阻尼孔时流场发生改变，影响到流体通过小孔产生的液阻（或压降）的大小。

根据本章阻尼器耗能机理分析可知，阻尼孔长决定了阻尼介质通过阻尼孔时流场的形态以及沿程能量损耗的多少，进而影响到阻尼器在工作时的阻尼力—位移滞回曲线形状以及最大输出阻尼力等性能参数。

通过试验可以看到（参见图3-18），保持输入位移幅值、激励频率和阻尼介质不变，随着阻尼孔长度的增加（S9阻尼孔长为45 mm，S7阻尼孔长为114 mm），相应的最大输出阻尼力增大，滞回环趋于饱满，耗能能力随之增大。

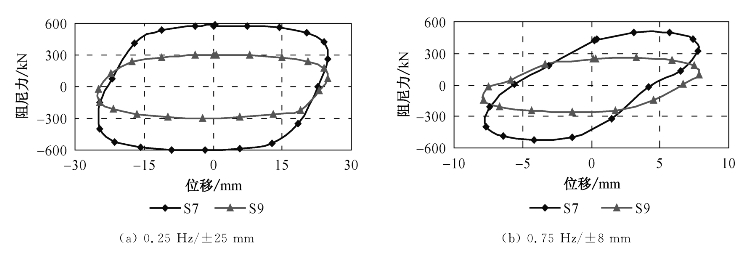
图3-18　阻尼孔长对性能的影响

5）环境温度对阻尼器性能的影响

保持激励频率、输入位移和阻尼介质不变，随着环境温度的改变，滞回环包络面积的大小有所变化，总体变化规律是，随着环境温度的升高，阻尼力有所减小（但是也有个别例外），然而降幅不明显（参见图3-19）。

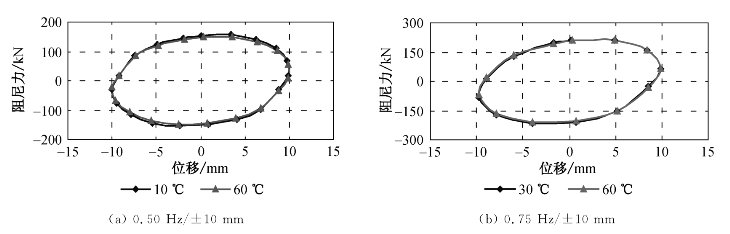
图3-19　阻尼器温度相关性能

图3-19为阻尼器S3在f=0.5 Hz、u0=±10 mm、f=0.75 Hz、u0=±10 mm及正弦波加载条件下，不同工作温度情况下的阻尼力—位移滞回曲线。由图3-19可知，阻尼器在不同温度环境下的工作性能比较稳定，对于阻尼器S3而言，其在10～60℃范围内，不同加载频率下，滞回曲线都比较饱满，最大阻尼力的波动范围在5%以内，耗能能力稳定。

对于在-20～10℃范围内黏滞阻尼器的力学性能，文献[9]中已做过相应的试验研究。试验结果表明，阻尼器的输出力在相同的外界激励作用下，受温度的影响也比较小。

6）阻尼介质充填质量对阻尼器性能的影响

由前述内容可知，阻尼器在正常工作情况下，性能稳定且可靠。但是在试验过程中也发现，如果阻尼器主缸内留有空隙（即阻尼介质未充满）时，阻尼器的力与位移之间的关系曲线在二、四象限产生缺口，将不能闭合为一个饱满的椭圆或类似椭圆的封闭曲线。

事实上，尽管在阻尼器的设计与制造过程中，考虑并采用了多道措施，例如同时设置灌油孔与排气孔，对小间隙部位灌油的特殊处理等手段，但在自然环境下要想完全去除阻尼介质中的气泡或溶解于阻尼介质中的气体（当环境温度升高时，气体将会析出）还是非常困难的，要达到这一目的，必须设计一套特殊的装备（包括真空设备，加压设备和阀的配合）和简便的操作流程。

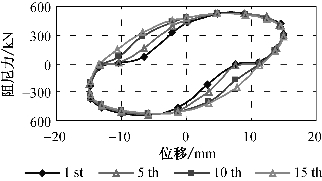
图3-20　未注满介质阻尼器循环加载性能

通过试验可以发现，对于阻尼介质未注满的阻尼器，在初始加载的情况下，阻尼力—位移滞回曲线在二、四象限会产生一些空缺，影响了阻尼器的耗能能力，但是在对阻尼器反复加载时，可以看到滞回环出现空缺的部位随着加载次数的递增，也在逐渐地得到补充，经过一定次数的循环加载，最终恢复为一个较为饱满的滞回环（参见图3-20，该图为阻尼器S8在f=0.25 Hz、u0=±15 mm及正弦波循环加载工况下的阻尼力—位移滞回曲线变化趋势）。

经分析认为，产生这一现象的主要原因是当阻尼器在反复加载时，一方面在一定压力作用下使得阻尼器内部各零件之间的配合间隙逐步为阻尼介质所填充；另一方面由于阻尼器将外界输入的机械能转化为热能耗散掉，阻尼介质的温度逐渐升高，使得阻尼介质内的气体慢慢析出并聚集于阻尼器内腔的上端，此时流经阻尼孔的介质所含气体或气泡已经越来越少，所以随着循环次数的增加，滞回曲线也逐步恢复饱满。

7）阻尼器刚度问题

通过对一定数量的阻尼器性能试验发现，多数情况下，阻尼器受到外界能量输入后，导杆带动活塞往复运动，外界激励衰减后，活塞随即停止运动，不像弹簧在外界作用力消失后恢复到初始状态，可见黏滞流体阻尼器基本无刚度。

但是随着阻尼器在工程上应用范围的不断扩大，对阻尼器性能（特别是对大吨位阻尼器）的要求也不断增多，因此需要对阻尼孔径等阻尼器内部构造不断做出调整或改变，这些措施会使活塞两端压差增大，活塞与阻尼通道构造复杂，如若外界激励频率提高或因大吨位要求阻尼孔道设计尺寸较小或阻尼介质黏度较大时，阻尼介质不能迅速由高压区域通过阻尼孔道流向低压区域，而活塞和导杆的运动为了同外界激励相谐调，必然会在高压下压缩阻尼介质，同时自身也发生微小的应变，这些应变累计起来形成阻尼器整体的弹性变形，从而使得阻尼器具有一定的瞬时刚度。

图3-21为阻尼器S3在正弦加载情况下的阻尼力—位移滞回曲线，随着加载频率的递增，滞回曲线由0.1 Hz时的呈双轴对称逐步发展到1.0 Hz情况下出现偏转，说明加载频率的高低会影响到阻尼器的瞬时刚度大小。

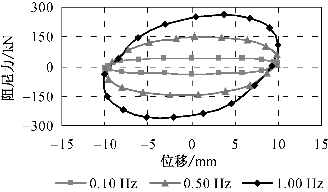
图3-21　阻尼器性能与加载频率关系

图3-6表明在相同的加载工况下，阻尼介质的黏度会影响到阻尼器的瞬时刚度。阻尼介质黏度越高，阻尼器在一定加载频率和幅值下出现的瞬时刚度也越大。

图3-15说明在相同的加载工况下，阻尼孔径的尺寸也会对阻尼器的瞬时刚度产生影响。阻尼孔尺寸越小，阻尼器表现出的瞬时刚度越大。

此外，瞬时刚度的大小还与阻尼介质和阻尼器活塞、导杆的弹性模量有关。尽管通常采用的阻尼介质不易被压缩，钢材的弹性模量也很大，但是大吨位阻尼器在工作状态时，传递给导杆、活塞的拉压力和阻尼介质的压强都非常大，使得阻尼介质、导杆和活塞产生一定的弹性变形，从而使得阻尼器表现出一定的瞬时刚度。