非牛顿流体阻尼器阻尼力计算公式

根据前述分析可知，阻尼器的耗能性能主要与黏滞流体在流动时的内摩擦力以及阻尼通道的构造形式有关。流体因为具有黏性，所以在运动过程中受到摩阻力的作用，为了克服这一影响，必然需要损失一定的机械能，即耗散外界输入的能量。

对于不同类型的流体，黏度与流体运动时剪切速度、剪切应力的关系不尽相同，所以其在运动过程中耗散能量的规律也不完全一样。式（3-27）给出了牛顿流体的F—V关系，在阻尼器的设计中，也常常选用非牛顿流体作为阻尼介质，因此也需要掌握非牛顿流体阻尼器的F—V变化规律。

由前文的介绍可知，非牛顿流体的种类较多，各自的本构关系也不同，对于其中的非时变性非牛顿流体（以下简称非牛顿流体），根据文献[4，14]可定义其剪应变速度函数为

或

由式（3-28）可得非牛顿流体的圆管沿流体流向速度分布的规律为

式中，u——距圆管中心轴r处的流体流速；

R——圆管截面半径；

C——积分常数。

根据黏性流体在管壁处流速为零，即边界条件为r=R，u=0，得到积分常数C为

因此

非牛顿流体管流的剪切应力分布规律为

式中，τ——距圆管中心轴r处的剪切应力；

τw——管壁处的剪切应力。

由式（3-31）和式（3-32）可得黏性流体流速的一般表达式为

由式（3-33）可得通过管长为L的流量Q为

对式（3-34）进行分部积分，得到

根据边界条件为r=R，u=0，可得

所以有

对式（3-37）的积分变量进行变换，可得

根据文献[4]可知，黏性流体剪切应力沿径向的分布规律为

式中，Δp——黏性流体经过长度为L的管道后的压力损失，也即管道两端的压差。

所以管壁处（r=R）的剪切应力τw为

由式（3-38）～式（3-40）可得

因活塞的相对运动速度为V，净截面面积为A，这里假定在活塞上共有n组孔径为d的阻尼圆孔（为方便设计和制造，阻尼孔的直径通常为同一尺寸，d=2R），根据流体连续性原理，得到

阻尼介质选定后，则根据其流体类型，可以确定剪应变速度函数f（τ）的具体表达式，经分析可知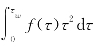是一个包含Δp、d、L、μ（或表观黏度η）等参数的表达式，故其实质为关于Δp的表达式。

因此，由式（3-42）得到活塞相对运动速度V与压降Δp之间的关系，为表述方便简洁，现定义其函数关系为

又因为F=Δp·A，最终得到采用非牛顿流体作为阻尼介质的阻尼器阻尼力F的理论计算公式为

根据以上分析可知，在对黏滞阻尼器进行设计或性能分析时，对于选用不同配方阻尼介质的阻尼器，其阻尼力F的理论计算公式可按以下标准流程推导得到：

（1）确定所选用阻尼介质的流体类型以及对应的本构方程f（τ）；(www.xing528.com)

（2）将其代入式（3-34）或式（3-41）得到圆管层流的流量Q；

（3）根据流体连续性原理，由式（3-42）、式（3-43）得到活塞相对运动速度V与阻尼孔两端压降Δp之间的关系；

（4）再代入式（3-44）得到相应黏滞阻尼器的F—V计算公式。假设调制的阻尼介质本构关系满足幂律方程，即

式中，k——稠度系数；

α——流动指数。

依据上述分析方法，将式（3-45）代入式（3-42），得到

对式（3-46）进行变换后，可以写成

将式（3-47）代入式（3-44）并整理后，可以得到采用幂律流体（Power-law Fluid）作为阻尼介质的黏滞阻尼器阻尼力F关于速度V的计算公式：

文献[15]中也得到类似的公式，令

则式（3-48）可以简写为

式（3-45）中，k、α均为常数，本构关系满足幂律方程的阻尼介质，如果α＜1，为剪切稀化流体，本章阻尼器配置的高黏度阻尼介质（硅油基黏滞材料-2以及硅油基黏滞材料-3）即为此类型流体；若α＞1，则为剪切稠化流体。如果α=1，k=μ，幂律方程则变换为牛顿流体的本构方程，故式（3-44）对于牛顿流体也同样成立，计算时只需将f（τ）=τ/μ代入公式，即可得到与式（3-27）忽略局部阻力损失影响后同样的结果：

如果黏滞阻尼器所选用的阻尼介质为宾汉流体（Bingham Fluid），则其本构方程为

式中，τ0——屈服值；

ηp——塑性黏度。

τ0、ηp在一定的温度和压力下为常数，根据宾汉流体的本构方程可知，对该类型流体施加的切应力只有超过屈服值τ0时才能产生流动，且切应力与应变速度呈线性关系。

同样根据以上推导方法，可以得到以宾汉流体为阻尼介质的黏滞阻尼器阻尼力计算公式为

令

则式（3-53）可以简写为

式中，Fb0表示使工作介质在阻尼孔内产生流动克服屈服应力τ0所需的初始力。

同理，对于满足卡森流体（Casson Fluid）本构关系的阻尼介质，有

式中，τc——卡森屈服值；

ηc——卡森黏度。

同样方法，可以得到卡森流体黏滞阻尼器阻尼力计算公式为

令

则式（3-58）可以简写为

通过以上分析与推导，得到了以非牛顿流体作为阻尼介质的黏滞阻尼器力学模型。在公式（3-44）的推导过程中，没有考虑流体局部阻力损失的影响，对于采用较高黏度阻尼介质的细长孔式黏滞阻尼器，由于阻尼孔道长径比较大，故这部分损耗在所耗散的总机械能中所占比重较小，为分析问题简便起见，近似忽略其影响。

需要说明的是，以上公式在推导过程中，借助了众多流体力学的基本理论，很多推导步骤具有相应的前提条件，也即最终的阻尼器F—V计算公式是在一定假定的基础上所得，该公式能否准确反映阻尼器的实际性能，还需通过试验进行验证或修正。