【任务内容】
最基本图形的作图方法。
【任务分析】
最基本的几何作图:线段、两平行线间、角、圆周等分的画法,以及弧线的连接等作图方法,了解椭圆的画法。
【任务实施】
一、等分直线段
等分线线段就是将一已知线段平均分成需要的份数,如图1-3-1 所示。
若该线段能被等分数整除,则可直接用三角板将其等分。如果不能整除,则可采用作辅助线的方法等分。
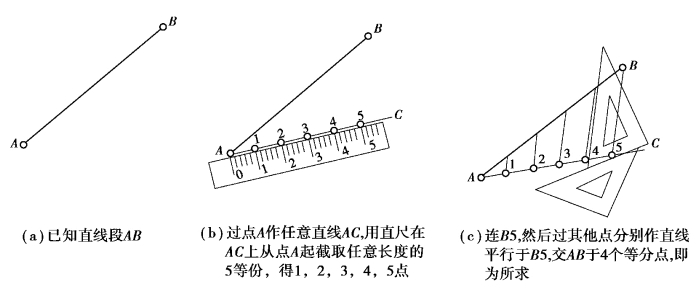
图1-3-1 等分线段
二、两平行线间的任意等分
两平行线间的等分方法如图1-3-2 所示。
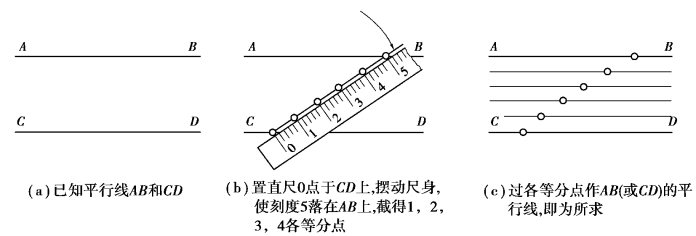
图1-3-2 两平行线间的等分
三、角的二等分
角的二等分方法如图1-3-3 所示。
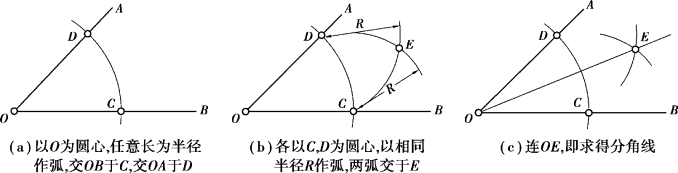
图1-3-3 角的二等分
四、等分圆周
将一圆分成所需要的份数,即等分圆周的问题。
作正多边形的一般方法是首先作出正多边形的外接圆,然后将其等分。因此,等分圆周的作图包含着作正多边形的问题。作图时,可用三角板、丁字尺配合等分,也可用圆规等分。在实际作图时,可采用方便快捷的方法。较常用的等分有三等分、六等分、十二等分及五等分。下面分别予以介绍。
1.三等分
用圆规作圆三等分,方法如图1-3-4 所示。

图1-3-4 用圆规作圆三等分
2.六等分
①用丁字尺和三角板作圆六等分,方法如图1-3-5 所示。
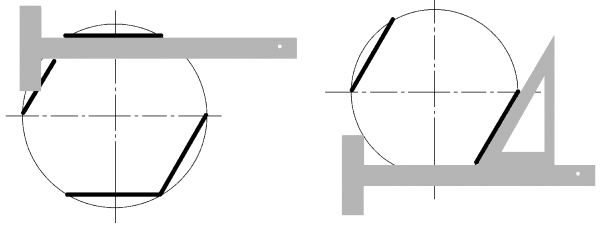
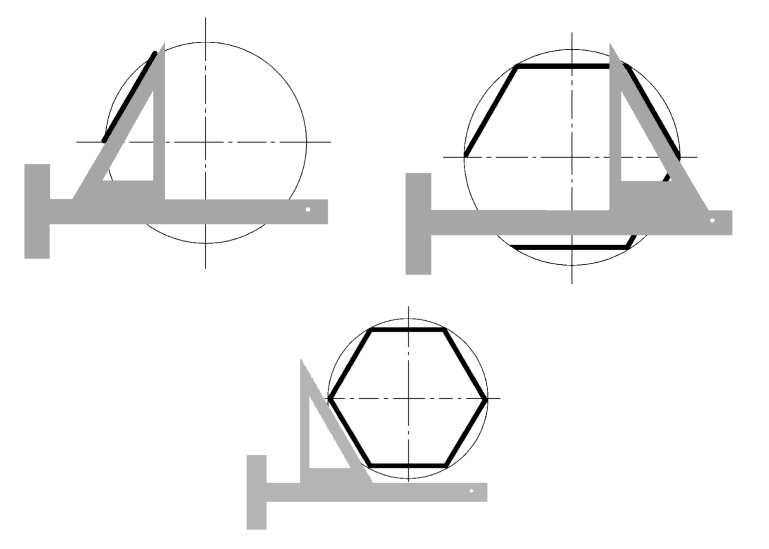
图1-3-5 用丁字尺和三角板作圆六等分
②用圆规作六等分,方法如图1-3-6 所示。
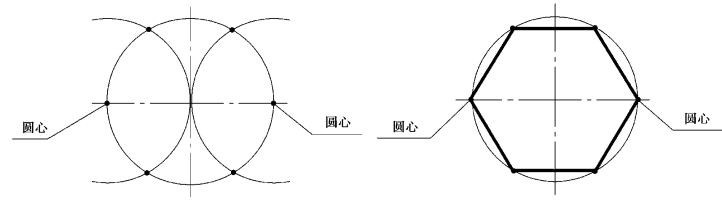
图1-3-6 用圆规作圆六等分
3.十二等分
圆十二等分是较为方便且等分数较多的一种等分方法。当需要在圆上找较多等分点时,就会用到此方法。
用圆规作圆十二等分,方法如图1-3-7 所示。
4.五等分
用圆规作圆五等分,方法如图1-3-8 所示。
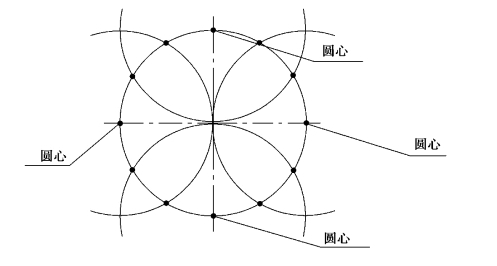
图1-3-7 用圆规作圆十二等分
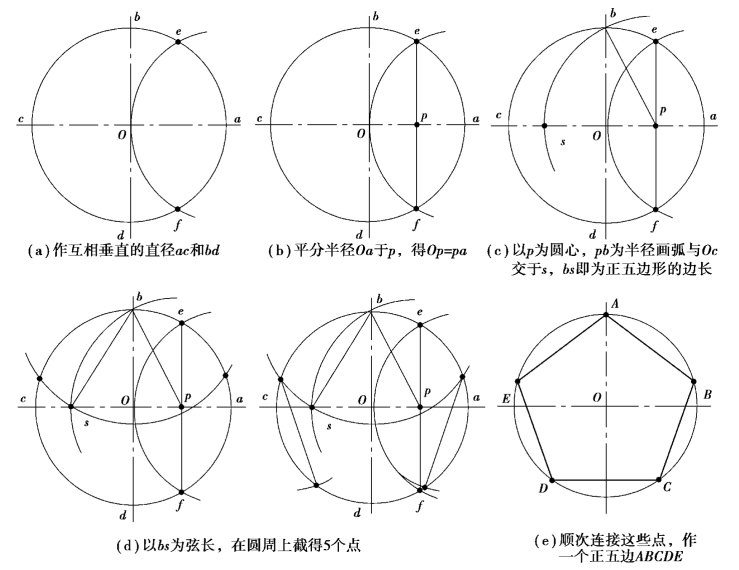
图1-3-8 用圆规作圆五等分
五、圆弧连接
同学们,看一看扳手的图形(见图1-3-9)如何画呢?
首先,要知道圆弧连接的实质是几何要素间相切的关系。作图时,需要解决的两个问题:
①确定连接圆弧圆心的位置。
②准确定出切点(连接点)的位置。
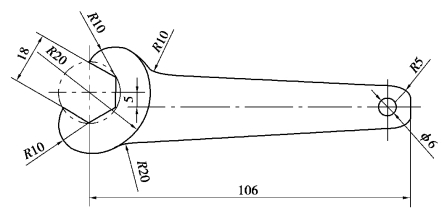
图1-3-9 扳手
其次,要知道圆弧连接的形式:
①用圆弧连接两已知直线。
②用圆弧连接两已知圆弧。
③用圆弧连接一直线和一圆弧。
1.用圆弧连接两直线
问题的提出:已知两直线L1,L2 以及连接圆弧半径R,试作出连接,如图1-3-10 所示。
回顾直线与圆相切的关系:
①圆心到两条切线的距离相等,等于圆的半径。
②过圆心作切线的垂线,垂足即切点。
作图步骤如图1-3-11 所示。
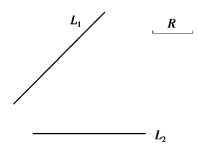
图1-3-10 圆弧连接两直线
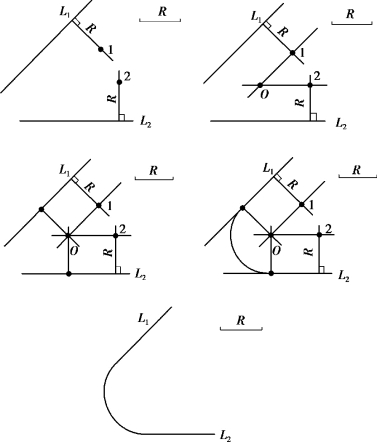
图1-3-11 圆弧连接两直线作图步骤
已知两已知直线L1,L2 垂直相交以及连接圆弧半径R,试作出光滑连接。
作图步骤如图1-3-12 所示。
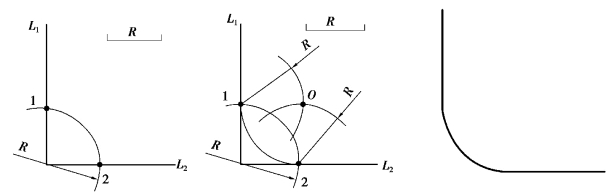
图1-3-12 两条直线交成直角作图步骤
2.用圆弧连接两圆弧
用圆弧连接两圆弧作图依据的是几何中两圆相切的基本关系。
1)圆与圆相切
(1)两圆内切(https://www.xing528.com)
两圆中心距等于两圆的半径之差,即
![]()
两圆心连线的延长线和圆的交点即切点,如图1-3-13 所示。
(2)两圆外切
两圆中心距等于两圆的半径之和,即
![]()
两圆心连线和圆的交点即切点,如图1-3-14 所示。
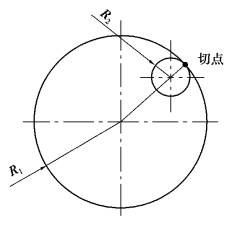
图1-3-13 两圆内切
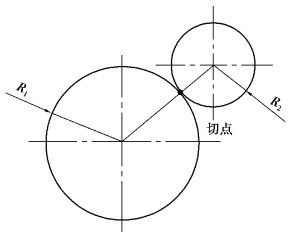
图1-3-14 两圆外切
2)用圆弧连接两圆弧
(1)外切作法
已知圆O1(半径R1)、O2(半径R2)连接圆弧的半径为R,如图1-3-15 所示。试完成连接作图(外切)。
作图步骤如图1-3-16 所示。
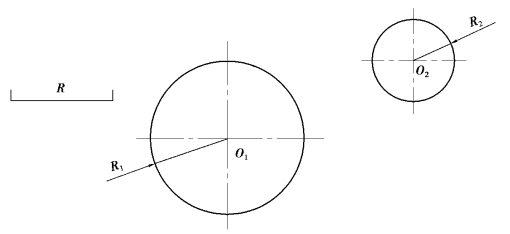
图1-3-15 用圆弧连接两圆弧外切
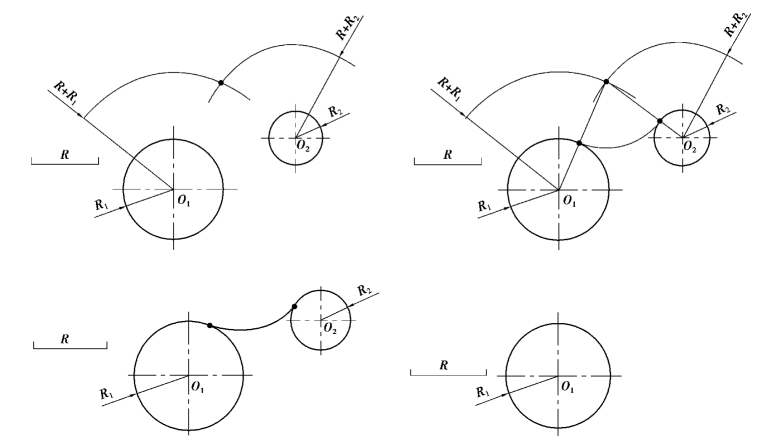
图1-3-16 用圆弧连接两圆弧外切作图步骤
(2)内切作法
已知圆O1(半径R1)、O2(半径R2)连接圆弧的半径为R,试完成连接作图(内切)。
作图步骤如图1-3-17 所示。
(3)外切和内切
已知圆O1(半径R1)、O2(半径R2)连接圆弧的半径为R,如图1-3-18 所示。试完成连接作图(与O1 外切,与O2 内切)。
作图步骤如图1-3-19 所示。
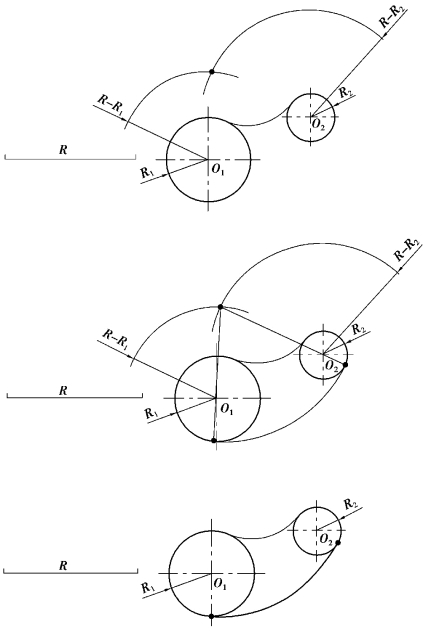
图1-3-17 用圆弧连接两圆弧内切作图步骤
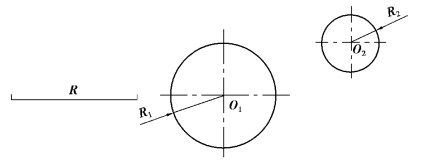
图1-3-18 外切和内切
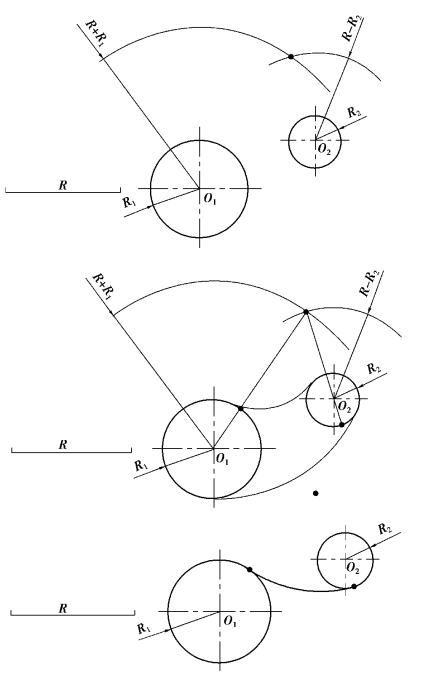
图1-3-19 外切和内切作图步骤
3.用圆弧连接直线和圆弧
连接直线和圆弧的作图方法同前面介绍的两种连接情况类似,即分别按照连接直线和圆弧的方法求出圆心和切点。下面举例说明。
已知一直线和圆O1(半径R1)连接圆弧半径为R,如图1-3-20 所示。试作出光滑连接(与圆切)。
作图步骤如图1-3-21 所示。
特别提醒:
①为能准确、迅速地绘制各种几何图形,应熟练地掌握求圆心和切点的方法。
②为保证图线连接光滑,在作连接圆弧前,应先用圆规试画。若有误差,可适当调整圆心位置或连接圆弧半径大小。
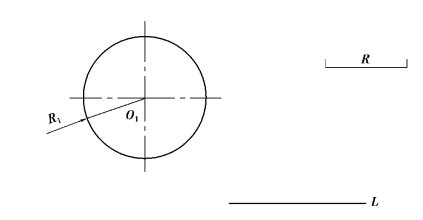
图1-3-20 用圆弧连接直线和圆弧
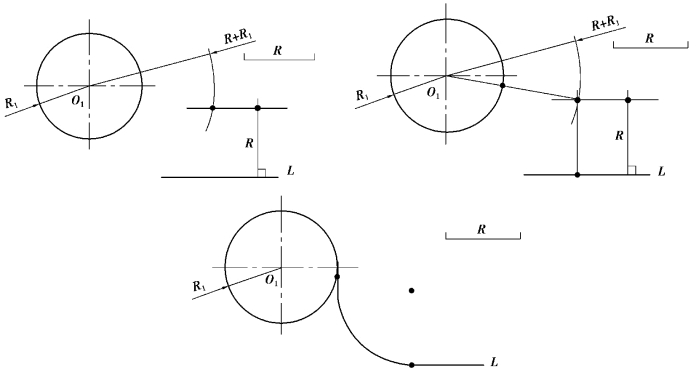
图1-3-21 用圆弧连接直线和圆弧作图步骤
【任务拓展】
椭圆的近似画法
椭圆是非圆曲线。由于一些机件具有椭圆形结构,因此,在作图时应掌握椭圆的画法。
椭圆画法较多,已知椭圆的长短轴(或共轭轴),如图1-3-22 所示;用四心圆法作近似椭圆,称为四心法,如图1-3-23(a)所示;用同心圆法作椭圆,称为同心圆法,如图1-3-23(b)所示。
一、同心圆法
用同心圆法画椭圆的基本方法是:在确定了椭圆长短轴后,通过作图求得椭圆上的一系列点,再将其光滑连接。
例1-3-1 已知长轴AB、短轴CD,试用同心圆法作出椭圆。
解:作图步骤如下:

图1-3-22 椭圆长、短轴
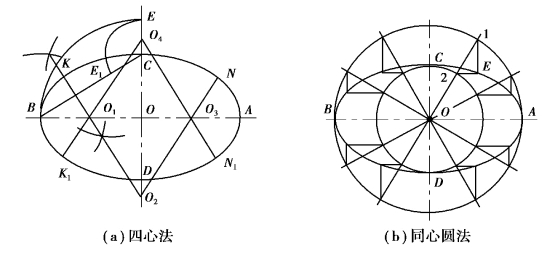
图1-3-23 椭圆的近似画法
①已知椭圆的长轴AB 和短轴CD,分别以这两个轴为直径画同心圆。
②将两个圆平均分为12 份。
③分别过小圆的等分点作水平线,过大圆的等分点作竖直线,其对应的交点就是椭圆圆周上的点,依次连接即可,如图1-3-24 所示。
二、四心法
四心法是一种近似的作图方法,即采用4 段圆弧来代替椭圆曲线。由于作图时,应先求出这4 段圆弧的圆心,因此,将此方法称为四心法。
例1-3-2 已知长轴AB、短轴CD,试用四心法作出椭圆。
解:作图步骤如下(见图1-3-25):
①画长短轴AB,CD,连接BC ,并取CF=OA-OC(长短轴差)。
②作BF 的中垂线与长轴、短轴上交于两点1,2,在轴上取对称点3,4,得4 个圆心。
③连接O1O2,O2O3,O3O4,O4O1,并适当延长。
④分别以O1,O2,O3,O4 为圆心,以O1A,O2C,O3B,O4D 为半径,顺序作4 段相连圆弧(两大两小,4 个切点在有关圆心连线上),即所求椭圆。
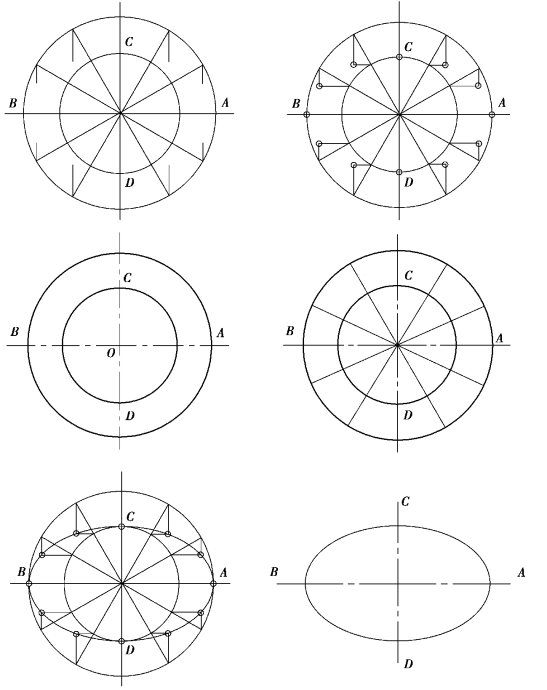
图1-3-24 同心圆法作图步骤
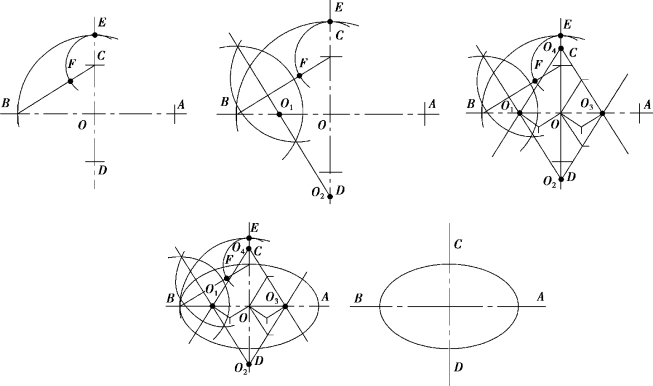
图1-3-25 四心法作图步骤
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




