轨道交通RAMS工程基础：可靠性增长模型

可靠性增长试验需要有增长模型，该模型可以是生产方可靠性增长试验的经验总结，也可以是合理的某个理论模型。

增长模型描述了产品在可靠性增长试验过程中可靠性增长的规律，它是制定可靠性计划增长曲线的依据，与可靠性增长试验相配合，依据故障次数或故障时间序列，在跟踪过程中能评估产品当前可靠性水平，在试验结束后能评估产品最终达到的可靠性水平，而不必在产品每一次改进设计、可靠性水平发生改变后，单独安排可靠性鉴定试验来验证其变动后的实际水平。

可靠性增长模型有很多类型，按增长方式分类，可分为时间函数和顺序约束模型；按故障数据性质分类，可分为连续型和离散型模型。目前，在可靠性增长试验中，较常使用杜安（Duane）模型和AMSAA模型。

1.杜安（Duane）模型

目前，在可修产品的可靠性试验中，普遍使用杜安（Duane）模型，它适用于许多电子和机电产品的可靠性增长。

杜安（Duane）模型是一个确定性的经验模型，不是统计模型，使用方便，但很多情况下存在估计精度不高及无法给出参数的瞬时估计及区间估计等缺陷。随着产品的不断进行改进，产品的平均故障间隔时间MTBF的变化与试验时间具有如式（5-5）所示的规律。

式中 M_R——产品应达到的MTBF（h）；

M_I——产品试制后初步具有的MTBF（h）；

T_I——增长试验前预处理时间（h）；

T——产品由M_I增长到M_R所需时间（h）；

m——增长率，其值小于1。

对式（5-5）两边取对数，可得lnM_R=lnM_I+m（lnT-lnT_I），采用双对数坐标纸作图，以MTBF为纵坐标，累积试验时间T为横坐标，则此式为一直线，如图5-7所示。

图5-7 杜安（Duane）曲线双对数坐标

图5-7中当前的MTBF（用M₀表示）与累积的MTBF（用M∑表示）的关系如式（5-6）。

这表明，在可靠性增长试验中任一时刻产品的瞬时MTBF（M₀）是累积MTBF（M∑）的1/（1-m）。由于累积MTBF在可靠性增长试验时是很容易计算出来的，利用式M₀=M∑/（1-m），就可求得产品在增长过程中的瞬时MT_- BF，这使得杜安（Duane）模型应用非常方便。

在进行可靠性增长试验之前，必须制定一个计划的增长曲线，作为监控试验数据的依据。

按杜安（Duane）模型制定计划增长曲线，首先必须选择M_I、T_I、m等参数。而后即可根据规定的可靠性要求M_R，确定增长试验时间T。

1）产品初始MTBF（M_I）可根据类似产品研制经验或已做过的一些试验（如功能、环境试验）的信息确定。一般为产品MTBF预测值（M_P）的10%～30%。(www.xing528.com)

2）增长试验前预处理时间T_I是根据受试产品已有的累积试验时间确定。一般情况下，当M_P≤200h时，T_I取100h；当M_P>200h时，T_I取50%的M_P。

3）增长率m是根据是否采取改进措施以及消除故障的速度和效果确定，0.3～0.7。当m=0.1时，说明增长过程中基本没有采取改进措施；当m=0.6～0.7时，说明增长过程中采用了故障分析和改进措施，得到预期的最大增长效果。

4）故障报告闭环系统。可靠性增长试验要求故障分析与纠正过程有可追溯性，故障报告闭环系统既保证了故障纠正过程有严格的关联，又提供了这种追溯要求。所有可靠性增长试验应与一个完善的故障报告闭环系统作为一个整体来运行。

2.AMSAA模型

AMSAA模型是把可修系统在可靠性增长过程中的故障数的累积过程建立在随机过程理论上，认为累积故障过程是一个非齐次泊松过程。即在试验时间段（0，t]内，受试产品发生的故障数r（t）是个随机变量。随着t的增加，r（t）会发生变化，这变化反应在r（t）的统计特性上，主要是它的数学期望和方差。这样就形成了一个随机过程，又称计数过程，用{r（t），t≥0}表示。

在给定时刻t，发生n个累积故障数服从非齐次泊松过程见式（5-7）。

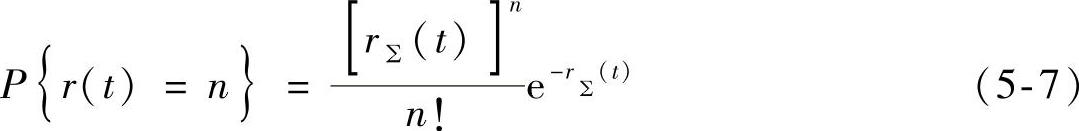
其中，，为累积故障的数学期望。

AMSAA模型认为在可靠性增长过程中，累积故障数是一个非齐次泊松过程，其故障强度函数见式（5-8）。

λ（t）=abt^b-1 （5-8）

式中 a——尺度参数，a>0；

b——形状参数，b>0。

杜安（Duane）模型与AMSAA模型在描述累积关联故障数对累积试验时间的关系上是极其相似的。杜安（Duane）模型用的是非随机变量的累积故障数，而AMSAA模型由于依据的是随机过程，其故障数是随机过程的数学期望，在参数转换后，AMSAA模型与杜安（Duane）模型的故障强度函数是完全相同的。因此，通常AMSAA模型是杜安（Duane）模型的概率解释。

AMSAA模型与杜安（Duane）模型在理论上有相同的不足之处：当t→0或t→∞时，AMSSA模型的故障率分别趋于零和无穷大，与工程实际不符。

3.可靠性增长模型选用原则

可靠性增长模型是用来制定增长计划、跟踪增长趋势及分析评价增长效果的工具，选取模型的原则是：

1）要根据产品寿命分布特征选择连续型或离散型模型。

2）应尽可能选择有物理意义的，简单、易操作的，且经过试验验证的模型。

3）所选择的模型应能够对试验结果进行评估。