1.ETA的分析步骤
(1)确定初因事件 确定和分析可能导致安全性和可靠性后果的初因事件并进行分类,对那些可能导致相同事件树的初因事件划分为一类。初始事件是事故在未发生时,其发展过程中的危害事件或危险事件,如机器故障、设备损坏、能量外逸或失控、人的误动作等,可以用两种方法确定初始事件。
1)根据系统设计、系统危险性评价、系统运行经验或事故经验等确定。
2)根据系统重大故障或故障树分析,从其中间事件或初始事件中选择。
(2)建造事件树 确定和分析初因事件发生后,可能相继发生的后续事件,并进一步确定这些事件发生的先后顺序,按后续事件发生或不发生(二态)分析各种可能的结果,找出后果事件。事件树的建造过程也是对系统的一个再认识过程;
(3)事件树的定量分析 对所建立的事件树,收集、分析各事件的发生概率及其相互间的依赖关系,定量计算各后果事件的发生概率,并进一步分析评估其风险。
2.事件树的建造
(1)常规事件树 考虑如图3-19a所示的桥式系统,由于系统中的各部件是连续运行的,后果事件与初因事件和后续事件的次序无关,因此在建立该系统的事件树时,可以选择任意一个部件作为初因事件。图3-19b为该系统的事件树,在图3-19b中由于每一个部件都有正常和故障两种状态,则其后果事件有25=32个。图中标记为S的后果事件为“系统成功”,标记为F的事件为“系统失败”,系统成功和系统失败的事件链各为16条。
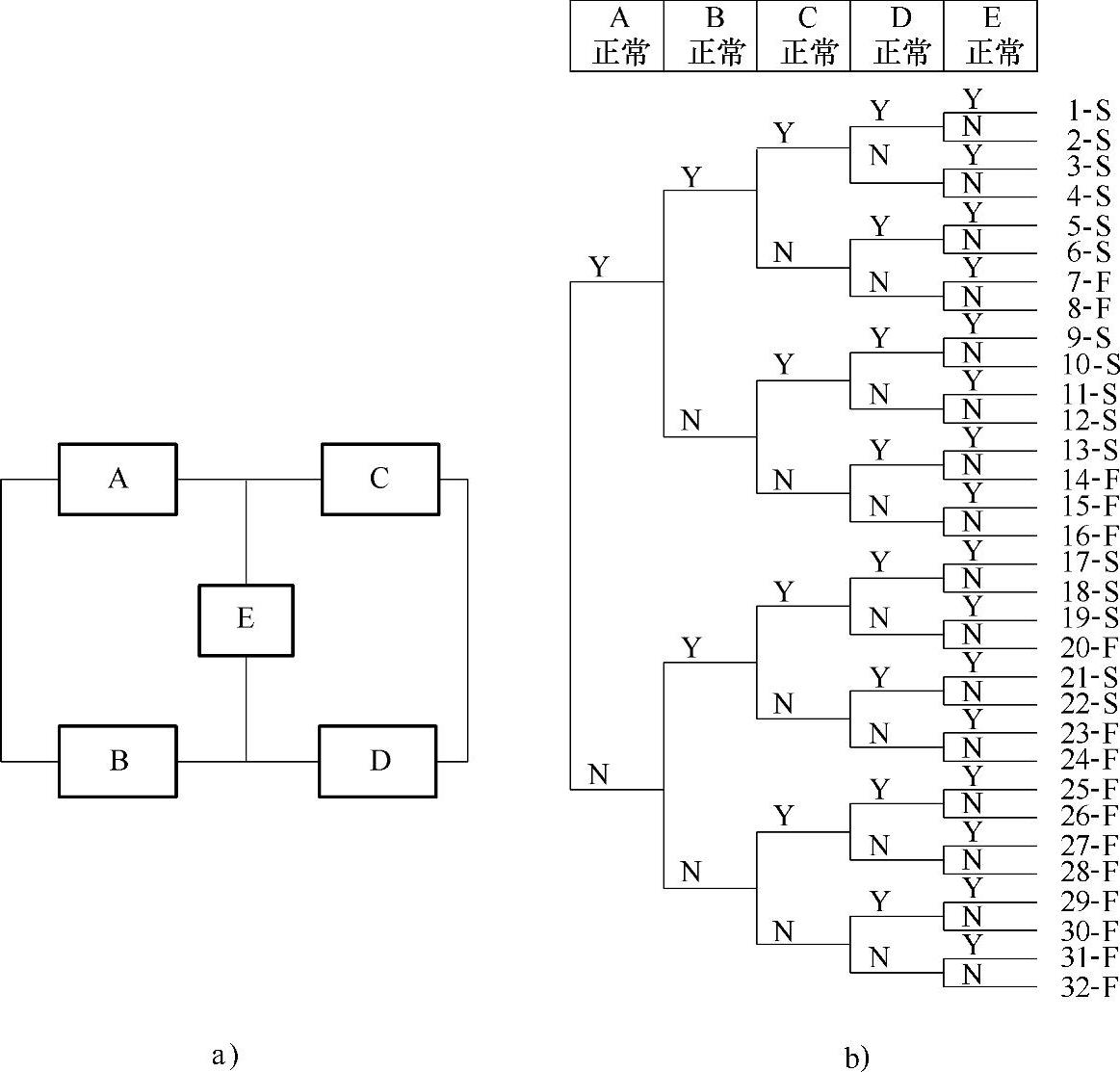
图3-19 桥式系统及其事件树
为了简化事件树,可以从系统正常的条件来判断,如当部件A、B正常时,那么只要有标记C正常,则系统就正常。因而部件D和E进一步分析就没有必要了。再如,部件A失效,同时部件B也失效,则该系统一定失效,因此也不必进行进一步分析,即可以得到一条系统失败的失效链。图3-20给出了该系统
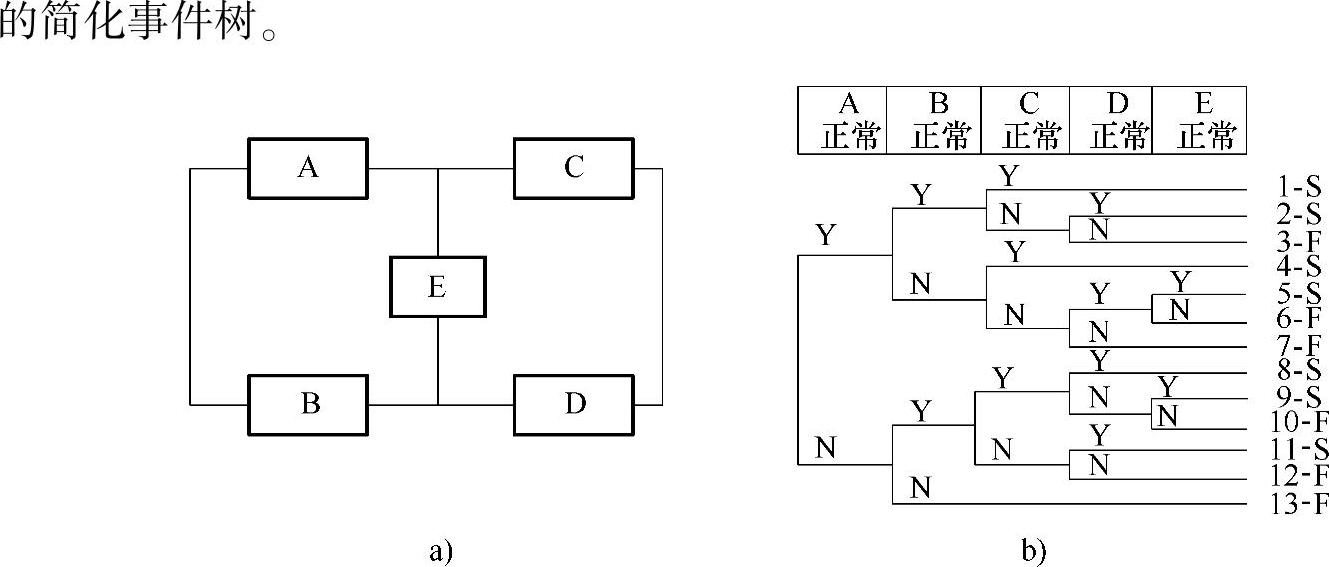
图3-20 桥式系统及其简化事件树
(2)冗余系统事件树 在冗余系统中,某一特定的初因事件发生后,其后续投入工作的部件是有一定的先后次序的。在构建这种事件树时,必须对系统进行较详细的功能分析以确定各后续事件发生的先后次序,才能建出正确的事件树。
如图3-21所示,在主断路器闭合控制电路中,当CCU接收到主断路器闭合的外部指令或接到通过分相区的信号时,在判定主断路器闭合条件满足后,通过MVB网络命令Sibas Klip Station(SKS1、SKS2,两个组成冗余结构,同时工作)闭合,同时通过VCB Activation Loop继电器(21-K25、21-K35)驱动主断路器的闭合电磁阀,导致压缩空气推动活塞杆运动,主断路器闭合。
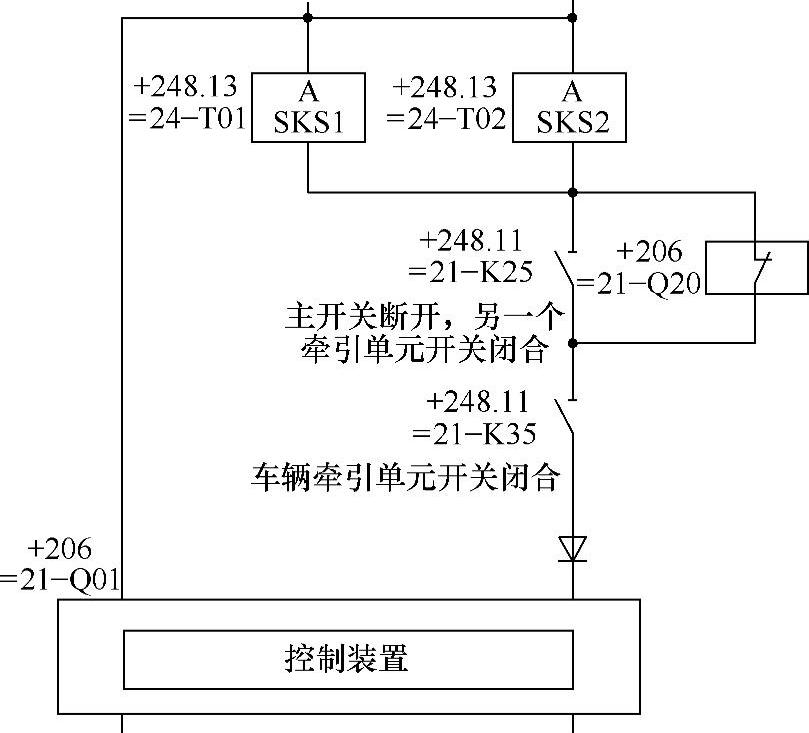
图3-21 主断路器闭合控制电路
21-K25的闭合条件取决于另外一个牵引单元的21-K35的闭合情况,若另外一个牵引单元(5、6、7、8车辆)的21-K35闭合,本单元(1,2,3,4车辆)的21-K25才闭合,当不满足上述条件时,则驾驶人在控制室控制隔离开关(10-Q20)断开,使得主断路器闭合。
在建造该电路的事件树时,由于SKS1与SKS2功能地位相同,则可任选任一作为初因事件,以SKS1故障为初因事件,该事件发生故障后要求SKS2正常,同时21-K35闭合,21-K25或10-Q20正常工作,主断路器才可以闭合。由于因此第一个后续事件必须为控制电路(CC)故障,其他的后续事件(无次序要求)可分别为SKS2故障、21-K35故障、21-K25故障、10-Q20故障,如图3-22所示。
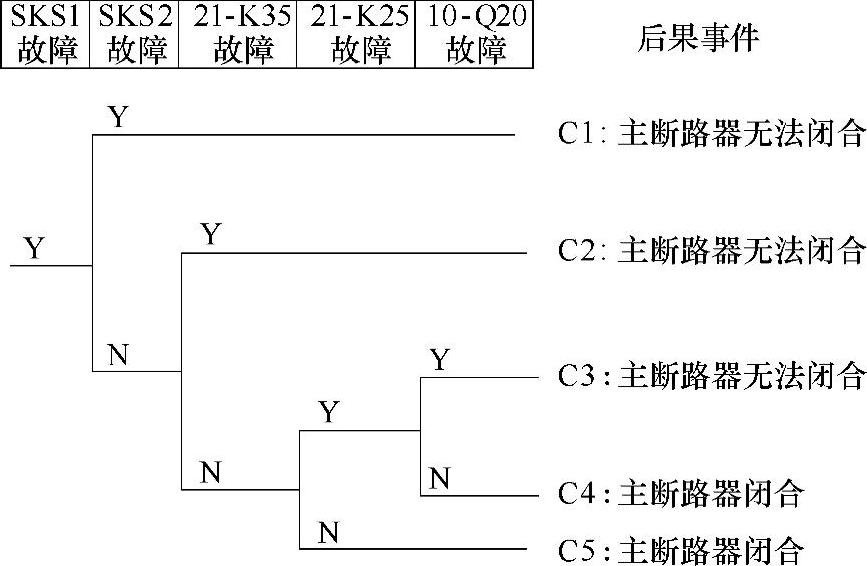
图3-22 主断器闭合控制电路事件树
(3)考虑人为因素的事件树 图3-23给出了车厢意外着火的事件树示例。在该例中,其后又发生火灾报警器故障、人员灭火失败、人员未能撤离等一系列事件。在该事件树中,将人员灭火失败、人员未能撤离等人为因素在事件树中一并进行考虑。
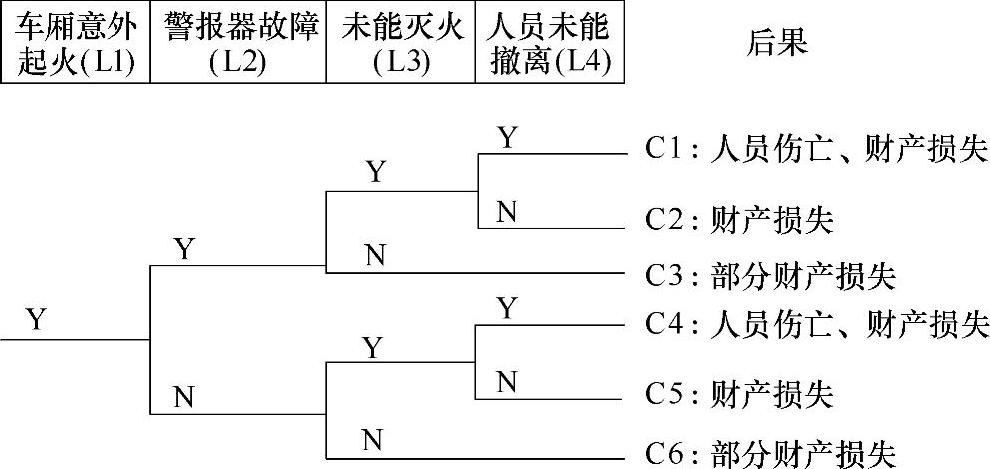
图3-23 车厢意外起火的事件树
在建立事件树的过程中,应注意有些事件链并没有发展到最后,即已结束。因此事件树的简化有以下两个原则:
当某一非正常事件的发生概率极低时可以不列入后续事件中;
当某一后续事件发生后,其后的其他事件无论发生与否均不能减缓该事件链的后果时,该事件链即已结束。
综上所述,在利用事件树对系统的可靠性、安全性进行分析时,最重要的是对系统的功能及外部因素进行详细的分析,确定初因事件、后续事件及其先后顺序、分析各种可能的事件序列并确定其后果,从而正确建立事件树。
3.事件树的定量分析
事件树的定量分析是计算事件树中的每一事件链分支的发生概率,并进一步评定这些事件链所造成后果的风险。事件树的定量分析主要步骤为:
① 确定初因事件的概率;
② 确定后续事件及各后果事件的发生概率;
③ 评估各后果事件的风险。
(1)确定初因事件与后续事件的发生概率 当初因事件或后续事件为系统中某一部件的故障事件时,其发生概率即为该部件发生故障的概率。对这一类事件可通过可靠性预计、故障树分析或使用统计等方法得出其故障概率。而当这些事件为某些外部因素时(如环境因素、人为因素等),其发生概率一般需通过长期的数据积累再经统计分析或评估得出。
(2)计算后果事件的发生概率 计算后果事件的发生概率可分为两种情况:其一,不考虑事件链中各事件的相依关系,其二,考虑各事件之间的相依关系。前者为简化计算,后者称之为精确计算。
1)简化计算:简化计算即不考虑事件相依关系的事件树定量计算。
考虑图3-18所示的两个系统的事件树,如果安全系统1和安全系统2相互独立,在工程系统中,安全系统的可靠性都较高,因此系统成功的概率接近为1。那么分别求出系统1和系统2的故障概率后即可计算出各种后果事件发生的概率:(https://www.xing528.com)
P(IS1 S2)=P(I)·P(S1)·P(S2)≈P(I)
P(IS1 F2)=P(I)·P(S1)·P(F2)≈P(I)·P(F2)
P(IF1 S2)=P(I)·P(F1)·P(S2)≈P(I)·P(F1)
P(IF1 F2)=P(I)·P(F1)·P(F2)≈P(I)·P(F1)·P(F2)
在工程系统中,若系统未定义为安全系统时,成功概率按原有值计算,如图3-19中后果事件发生概率的计算方法如下:
P(1-S)=P(SASBSCSDSE)=P(SA)·P(SB)·P(SC)·P(SD)·P(SE)=RA·RB·RC·RD·RE
P(2-S)=P(SA SB SC SD FE)=P(SA)·P(SB)·P(SC)·P(SD)·F(SE)=RA·RB·RC·RRDFFE
……
例如,对图3-19所示的系统,若假定系统中的各部件的故障是独立的,则可以计算出该系统的可靠度为
RS==Pi(3-31)
其Pi是后果事件,为系统事件链的成功发生概率,i=1,2,3,…,32。
各事件链的发生概率可由各部件的可靠度Rj和不可靠度Fj(j=A,B,C,D,E)求出,即:
P1=RA·RB·RC·RD·RE (3-32)
P2=RA·RB·RC·RD·FE (3-33)
若各部件的可靠度RA=RB=RC=RD=RE=0.99,则系统的可靠度RS=0.999798。
2)精确计算:精确计算即考虑事件相依关系的事件树定量计算。
当事件树中的各事件的发生不是相互独立时,进行事件树中后果事件发生概率的计算将更为复杂,此时必须考虑各事件发生的条件概率。以图3-18中的事件树为例,后果事件IF1 F2的发生概率为
P(IF1F2)=P(I)·P(F1/I)·P(F2/F1,I)
P(F1/I)表示在初因事件I发生的条件下,系统1失效事件(F1)发生的概率。而P(F2/F1,I)表示在初因事件I发生、系统1失效事件(F1)也发生的条件下,系统2失效事件(F2)发生的概率。
若P(I)=0.065,P(F1/I)=0.02,P(F2/F1,I)=0.03,则P(IF1 F2)=3.9×10-4
事件树中各事件具有相依关系的原因有多种,其具体计算的公式变化较大,且由于其应用不广泛,本文不再详细展开。
(3)后果事件的风险评估 以上介绍的均为如何计算各后果事件的发生概率,但为了评价后果事件的风险,需要对每一后果事件进行风险评估。事件的风险定义为事件的发生概率与其损失值的乘积:
R=P×C (3-34)
式中 R——后果事件的风险值;
P——单位时间内后果事件的发生概率;
C——后果事件的损失值。
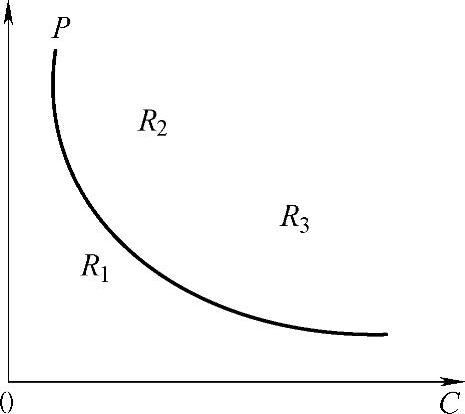
图3-24 法墨曲线示意图
如果后果事件的损失可以用一个确定的值来表示(一般情况下可以采用后果事件造成的损失费用),则可以计算出每一个后果事件的风险值。在衡量某一后果事件的风险时,一般采用法墨曲线进行,法墨曲线形式如图3-24所示。对于复杂系统一般需根据设计要求确定一个可接受的风险值,该值在法墨曲线中构成一条等风险线,若某一事件的风险值落在等风险线上方,如图3-24中的R2、R3,该事件的风险是不能接受的,需要采取措施进行改进,要么降低其发生概率,要么降低其后果损失。反之,若某一事件的风险落在等风险线下方,如图3-24中的R1,则该事件的风险是可接受的,可不进行改进。
4.注意事项
1)全面调研、广泛了解被分析对象的功能、外部因素及其事件全过程等,这是ETA的重要基础。
2)建造事件树是ETA的关键,应抓住其中4个环节,即:初因事件、后续事件、事件树和定量分析。
3)抓好事件树事件链的简化工作,其简化过程按下述两个原则进行:
① 当某一非正常事件的发生概率极低时可列入后续事件中;
② 当某一后续事件发生后,其后的其他事件无论发生与否均不能减缓事件链的后果时,即认为该事件链已结束。
4)后果事件的风险定量评估中,其损失值既可以用损失费用来衡量,也可采取其他值表达。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




