热拌沥青混合料密级与矿料分布研究

分形理论是定量描述几何形体复杂程度及空间填充能力的一门新兴边缘科学。目前，分形理论已经被广泛运用于研究自然界中常见的、不稳定的、不规则的现象。沥青混合料是由沥青、矿料和矿粉组成的非均质、多相、多层次的复合体系，其宏观力学行为呈现出不确定性、不规则性、模糊性和非线性，这正是分形研究的范畴。因此，分形理论已经成为研究沥青混合料的得力方法。矿料分布是否满足分形特征——自相似性和标度不变性，造成一些研究中分维值不能精确描述混合料微观结构，使得分维值和宏观性能的相关性不好。为了进一步分析分维值与沥青混合料性能的关系，本书首先进行密级配沥青混合料矿料分形分布特征研究。

1.矿料分形分布模型

设矿料的颗粒粒径为r，粒径不大于r的颗粒数目为N（r），根据分形理论有

式中　C——常数；

　　　D——颗粒粒径分形维数。

从而可以定义颗粒粒径分布函数为

式中　F（r）——颗粒粒径分布函数；

　　　N0——颗粒总数。

级配碎石的粒径分布可以采用各粒径矿料的质量分布函数表示，即

式中　P（r）——各颗粒粒径的质量通过率，%；

　　　M（r）——粒径不大于r的矿料质量，g；

　　　M0——矿料总质量，g。

则矿料级配的分形公式为

式中　rmin——最小颗粒粒径；

　　　rmax——最大颗粒粒径。

一般情况下，当颗粒粒径r相对于rmin较大时，rmin可以忽略，从而式（5.6）变为

可以看出上述的简化式（5.7）与富勒（Fuller）及泰波（Talbot）根据试验提出的公式具有相同的表达形式，从而揭示了分形维数和常用的K法等确定级配的方法具有统一的内涵，可从微观层面上解释级配的分布特征。

2.矿料分布分形相似性判定

由于石料在破碎时表现出相似的“破碎”效应，因此，其粒度分布必然具有相似性，只是相似程度的大小不同而已。另外，四川大学的谢和平等从分形几何的观点出发，对岩样破碎后的粒度分布进行了统计分析表明，岩石的粒度分布是统计意义上的分形。此外，满足自相似的结构一定满足标度不变性。本研究采用“Fuzzy分形集合”来研究矿料分布分形的相似性和标度不变性。

（1）分形集。分形是其组成部分以某种方式与整体相似的形。这里我们用集合思想来表达这一概念。假定Ai（i=1，2，…，n）为集合A的子集，且。若将Ai适当放大（或缩小）ri倍后与A完全重合，即集合A完全自相似，则A为分形集。其分维Df由式（5.8）定义：

(www.xing528.com)

反之，若将Ai适当放大（或缩小）ri倍后与A完全不重合，即集合A完全无自相似性，则A为非分形集。

（2）模糊（Fuzzy）分形集。由于“完全重合”与“完全不重合”之间，不存在明确的边界。由“完全重合”到“完全不重合”中间经历了一个从量变到质变的连续过渡过程。所以，对于大量存在于自然界中的分形集不能用经典集合论，仅取0或取1两个值的特征函数来刻画。为了刻画类似问题中的这种连续过渡过程，美国控制论专家L.A.Zadeh于1965年将经典集合论里特征函数的取值范围由{0，1}推广到闭区间[0，1]，得到了Fuzzy集的定义。

设在论域U上给定了一个映射：

则称A为U上的Fuzzy集，A（u）称为A的隶属函数。

于是，Fuzzy分形集的概念可表述为：假定Ai（i=1，2，n）为集合A的子集，且，若将Ai适当放大（或缩小）ri倍后与A的重合程度为A（u），则A为Fuzzy分形集。其分维Df亦可由式（5.10）定义：

由Fuzzy分形集的定义可知，对于某个Fuzzy分形集A，若A（u）仅取0和1这两个数时，A（u）就蜕化为经典分形集。若A（u）=1，则集合A具有严格的自相似性，例如Cantor集、Koch曲线等。若A（u）=0，则集合A无自相似性。若A（u）∈（0，1），则集合A的自相似性是近似的或统计意义上的自相似，这种自相似性大量存在于自然界中。例如，频繁演变的海岸线、级配骨料的粒度分布、水泥基材料的孔隙形貌特征、混凝土的断裂表面等都是模糊分形系统。

（3）矿料级配分布相似性判定。如前所述，矿料级配的分布具有Fuzzy自相似性和Fuzzy标度不变性，所以其分维数必然具有模糊性，我们用“Fuzzy分维”来表达这一概念。

对式（5.7）两端去对数，ln P（r）与ln r近似呈线形关系，其斜率b=3-D，则其模糊度d可定义为

式中　R 2——离散点的线性相关系数。

若d≡0，则该分形集具有严格的自相似性和严格的标度不变性。若d≡1，该集合不是分形集。若d∈（0，1），则该分形集为Fuzzy分形集。同大量存在于现实中的物质一样，矿料级配可视之为一个Fuzzy分形集，其模糊度d∈（0，1），它刻画了矿料级配分布自相似程度的大小，模糊度d越小，自相似的程度越大。

3.密级配沥青混合料矿料分布分形特征

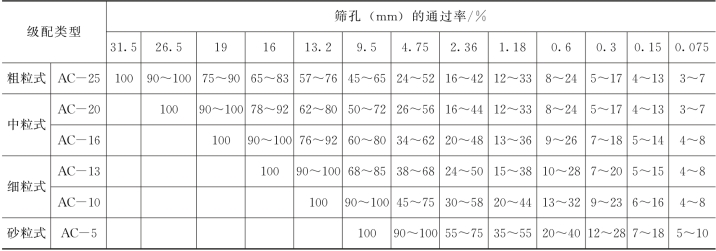
本研究以现行沥青路面施工技术规范中密级配沥青混凝土混合料矿料级配（见表5.10）为例，对表征矿料分布分形特征的两个重要内容——分形维数和各级配分形分布的自相似性进行研究。

表5.10　密级配沥青混合料矿料级配范围

（1）密级配沥青混合料矿料级配分形维数计算。根据矿料级配组成的数值，在矿料级配的双对数坐标图（图5.9）上（其中，横坐标为各级粒径与公称最大粒径比值的对数，纵坐标为各级粒径的通过率的对数），利用最小二乘法对级配曲线进行最佳直线拟合，求出通过率与筛孔之间的最佳拟合直线的斜率b，再利用3-D=b，即可求得沥青混合料矿料粒径分维值D。各组级配对应的分维值见表5.11。

图5.9　密级配沥青混合料矿料级配的双对数图

由图5.9可以看出，各组级配的和都呈现出较好的线形关系，说明密级配沥青混合料中矿料的分布呈一重分形分布。此外，在同一尺度范围内，级配上限较级配下限具有更高的分维数，可见矿料级配分形维数可以表征矿料级配的粗细。对于各级配的上限，分形维数大小在2.51～2.59内变化，且随着公称最大粒径的增加，分维数在逐渐减小，对于各级配的下限，分形维数大小在2.33～2.39内变化，亦即密级配沥青混合料矿料级配分形维数在2.33～2.59范围内变化。

（2）密级配沥青混合料矿料级配分形分布自相似性。根据前述密级配沥青混合料矿料级配分形维数计算中线性回归的相关系数，按照式（5.11）。计算各组矿料级配的模糊度，以对级配的分形分布自相似性进行评判。

从表5.11中可以看出，AC-25、AC-20、AC-16、AC-13等几组矿料级配的分形模糊度均小于0.02且级配上、下限的差异小于0.01，说明这几组级配的分形特征明显且上、下限的自相似性和标度不变形差异不大，在实际应用中可直接利用分形维数分析由这几组矿料级配范围内的矿料拌和的沥青混合料的相关性状。而最大公称粒径较小的AC-10和AC-5级配上、下限的模糊度差异较大，说明这几组级配上、下限的自相似性和标度不变形差异较大，这主要是由于两组级配下限的模糊度很小造成的。但总体来看，两组级配的模糊度均小于0.05，仍表现出较好的分形特征——自相似性和标度不变形。

表5.11　不同级配类型矿料的分维数和模糊度