如何确定权重系数,即准则对决策结果的贡献大小或者成为影响程度大小,是空间多准则决策结果准确性的重要前提。而在空间多准则决策过程中,需要对空间中同一位置的同一准则都赋予同一权重值,这样才能在决策的过程中实现对每个准则能够较好反映。因此,准则权重的选择对决策结果有重要影响。目前有许多确定权重的方法,如排序法(Ranking Method)、成对比较法和方差最大化等方法。
1)排序法
作为一种最简单的确定权重的方法,此方法属于主观赋权法,主要依赖于决策者的经验[231-236]。首先对决策准则按照重要性程度进行排序,最重要的,n=1,次重要的n=2,等等,第n重要的值为n,然后进行计算,其计算可以采用多种方法,其中比较常用的为求和法:

式中,wk为第k项准则的权重,n是准则的数目,pk是准则的排序。此方法也被在多处应用,基于此方法,Sharifi等建立了ILWIS-SMCE决策模型;Ozturk和Batuk开发了基于ArcGIS的多准则分析程序[237]。
2)成对比较法
其中,在1980年,Saaty在层次分析法(Analytic Hierarchy Process,AHP)的基础上开发了成对比较法,主要采用根据经验定义1到9的值来对准则的重要性程度进行比较[231],见表6-1,通过对准则的两两比较,建立一个比较矩阵:C=[ckp]n×n,ckp为两两比较的第k项和第p项准则。矩阵C是一个正互反矩阵,cpk=c-1kp,所有对角线上的元素都等于1,即当k=p时,ckp=1,因此只需要进行n(n-1)/2对的实际比较即可,当建立了比较矩阵以后,权重向量w=(w1,w2,…,wn)可以被计算出来。定义λmax为矩阵C的最大特征根,则
![]()
虽然Saaty提出了许多方法来求解权向量,但是目前比较常用的是归一化求解方法,首先对矩阵C进行归一化或者标准化处理:
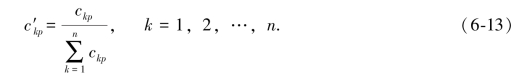
权重可以通过如下式求解:
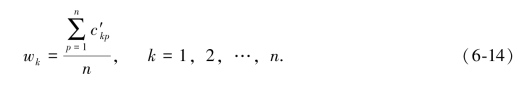
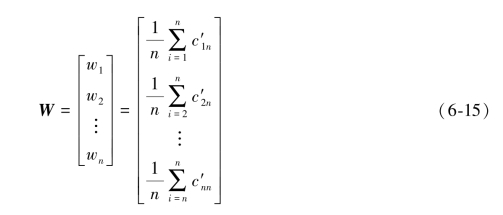
表6-1 成对比较的评价值[231]

由于比较矩阵的建立是在决策者的经验判断的基础上,为了保证权向量的准确程度,可以采用一致性检验的方法,对构建的矩阵进行检验,一致性检验的指标可以定义为:

对照表6-2查找一致性检验指标值。
表6-2 一致性检验指标值

计算一致性检验比例CR:

当CR<0.1时,比较矩阵的一致性符合要求。当CR≥0.1时,比较矩阵的一致性不符合要求,需要对比较矩阵C的数据进行调整。
3)基于熵(Entropy)的准则权重计算方法
与排序法、成对比较法以及方差最大化方法不同,基于熵的权重求解方法是一种客观的求解方法,不需要根据决策专家的经验,此方法主要是基于信息熵来进行计算的。熵可以用来度量信息,因此准则的权重可以被认为是连续的信息,我们可以通过计算每个准则中信息的含量来计算准则aik的权重,其信息量用熵来度量,定义为Ek:
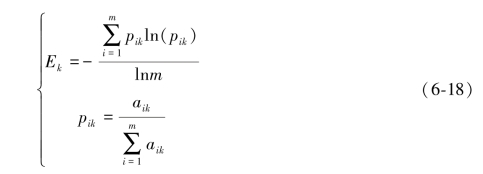
一组准则中包含信息的多样性程度可以定义为bk:
![]()
基于熵的准则权重可以定义为:

基于熵的权重可以与其他方法求得的权重wk相结合,可获得新的权重的定义:
 (https://www.xing528.com)
(https://www.xing528.com)
显然wEk和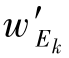 的范围为0~1之间,准则包含的信息种类越多,其值越高。准则的熵值越小,其多样性程度越大,这意味着此项准则提供的信息越多。如果某项准则是均匀的,即为一个定值,其准则权重为0,此项准则可以不作为决策准则,因为它不传递有关决策情况的信息。基于熵的权重确定方法是一种有效的多尺度的可以适用于GIS空间决策的分析方法。其能够很好地与WLC(Weighted Linear Combination)相结合进行空间决策[238-239]。
的范围为0~1之间,准则包含的信息种类越多,其值越高。准则的熵值越小,其多样性程度越大,这意味着此项准则提供的信息越多。如果某项准则是均匀的,即为一个定值,其准则权重为0,此项准则可以不作为决策准则,因为它不传递有关决策情况的信息。基于熵的权重确定方法是一种有效的多尺度的可以适用于GIS空间决策的分析方法。其能够很好地与WLC(Weighted Linear Combination)相结合进行空间决策[238-239]。
4)离(方)差最大化(M axim izing Deviation)
根据信息论的原理[240],如果某一准则在每一排水平使决策对象无显著差异,标准无关的不同等级水平的多准则决策评价对象的排序[241]。如果准则使决策对象有较大差异,则此准则对决策结果有较大贡献,起比较重要的作用。可以用准则的方差来表示某准则对决策对象的偏差影响。对于准则yj,Dij(w)表示不同评价对象之间的偏差:
![]()
定义总偏差TD j(w):
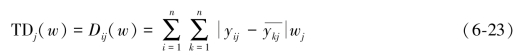
式中,w是权重系数,且w=(w1,w2,…,wn)T>0,满足单位化约束条件:

然后目标函数可以定义为:
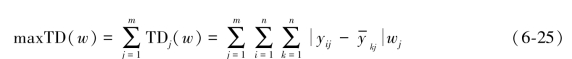
结合式(6-24)与式(6-25),求解wj的问题即为求解方程组最优化解的问题。求解此联合模型[242]:
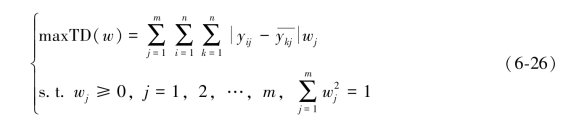
可求得目标函数的极大值点,w′j:
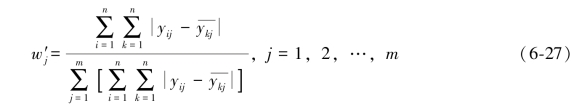
传统的权重系数可以定义为:
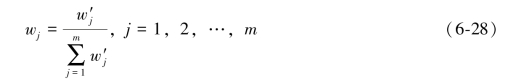
对其进行归一化处理,最终可得:
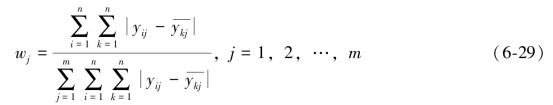
此种方法需要对获得的权重信息进行归一化处理,适用于权重完全未知的情况,当部分权重信息已知时,无法考虑,对决策结果的准确性有一定影响,因此可构造方差目标函数,对权重进行计算,通过计算决策目标离差的平方,即方差[242]:
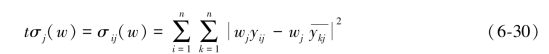
构建如下最优化求解问题:
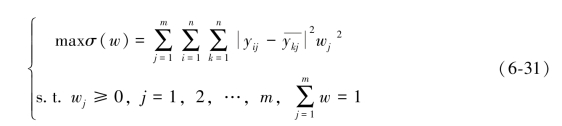
我们引入拉格朗日(Lagrange)函数来求解此模型:
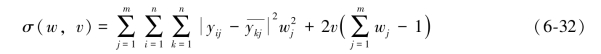
式中,v为拉格朗日算子。求其偏导数,并令:
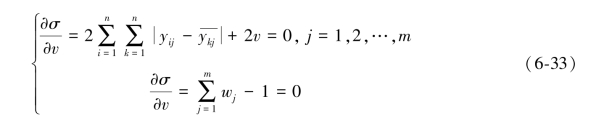
最后,可得最佳权重方程:
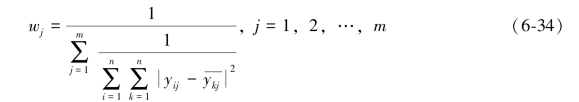
如果可以确定某项准则的影响程度,比如某项准则的影响程度很小,但是实际取值时计算出影响程度较大[209],此时可以根据经验对准则限定范围0≤aj≤wj≤bj,其中aj和bj分别为wj的下限和上限,可以通过求解下面的线性规划模型求解权向量。
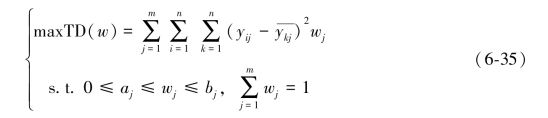
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




