为了研究在工作面推进过程中,每步开采操作导致的应力重新平衡所伴随的裂隙的时空演化规律,本研究以图4-9所划分网格为统计单元,研究网格内裂隙在推进过程中的分形维数和裂隙熵的时空变化规律,建立采动覆岩裂隙分形维数和裂隙熵的时空立方体模型,如图4-32(a)和图4-33(a)所示,并对其进行Man-Kendall趋势分析,获得2020个具有估计观测值的位置,20200个已估计的全部观测值。Z得分为3.94,表明随着时间的推移采动覆岩分形维数和裂隙熵整体上具有递增趋势,采动覆岩裂隙系统是个熵增加的过程。
新兴时空热点分析可识别数据中的趋势,例如,其可发现新的、加强的、缩减的以及分散的热点和冷点。时空热点分析也被应用于采动覆岩裂隙时空演化分析中,其中时空热点表示裂隙分形维数或裂隙熵发生的高值点在时空中的聚集,而时空冷点即为裂隙分形维数和裂隙熵发生的低值点在时空中的聚集。可以通过新兴时空热点分析探测采动覆岩裂隙演化过程中存在的冷热点及其特征,评估这些冷热点随时间的变化趋势。热点分析对数据集中的每一个要素计算Getis-Ord Gi*统计(称为G-i-星号),可以得到高值或低值要素在空间上发生聚类的位置。Getis-Ord Gi*局部统计量可以对数据集的局部空间自相关性进行检测,分析其临近空间的聚类关系,得到时空对象属性分布的热点区域或冷点区域。Getis-Ord局部统计可以表示为:
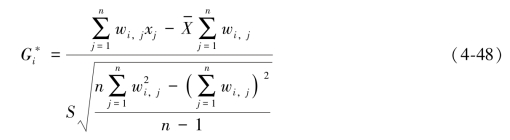
式中,xj是要素j的属性值,wi,j是要素i和j之间的空间权重,n为要素总和,且
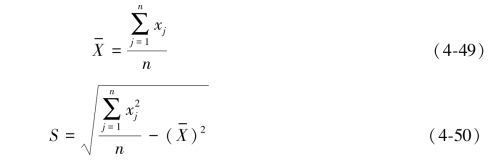
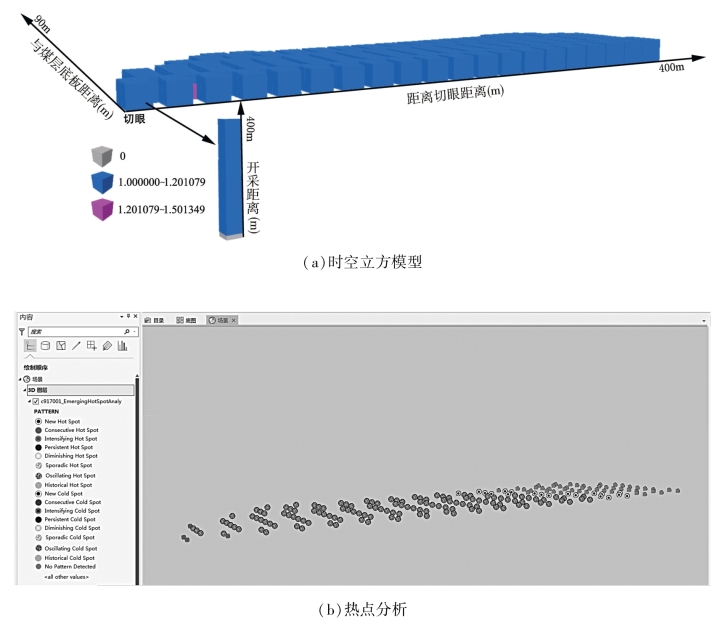
图4-32 采动覆岩裂隙分形维数的时空立方及热点分析
高值点并不一定都是统计意义上的显著性热点,通过分析每个位置或空间网格上的Getis-Ord Gi*统计得分的时间序列,然后分析这些位置的热点和冷点特征,并对其趋势进行评估。分别对采动覆岩裂隙的分形维数和裂隙熵进行热点分析,结果如图4-32(b)和图4-33(b)所示,新增热点主要集中在工作面推进方向的上方与前方,主要反映了新裂隙的产生,裂隙的方向也发生改变,以及覆岩的变形破坏。对于采动覆岩裂隙分形维数来说,在切眼和工作面之间主要分布振荡的热点,即其具有冷点历史,说明了在工作面推进过程中,工作面后方、采空区及其上方的覆岩裂隙由于采动的影响,无论是在时间还是空间上均有裂隙产生、张开、闭合、压密和贯通等发生。而裂隙熵在工作面后方、采空区及其上方主要分布连续热点,也说明了覆岩裂隙受采动的影响,无论是在时间还是空间上均有裂隙的张开、闭合等发生,但是没有分形维数的振荡热点多,因此采动覆岩裂隙分形维数和裂隙熵可以用来表示裂隙时空状态及其时空演化特征。
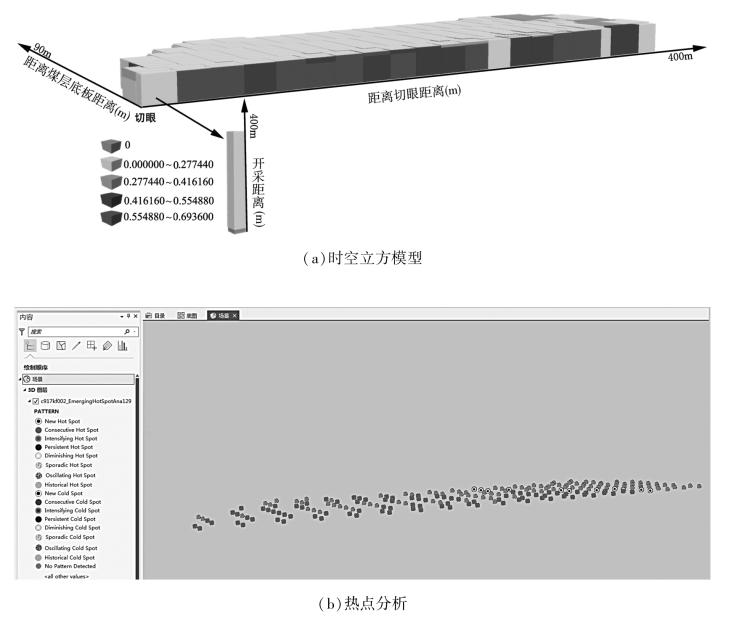
图4-33 采动覆岩裂隙熵的时空立方及热点分析(https://www.xing528.com)
某一单元内的裂隙分形维数增加,即说明此单元的裂隙长度占位空间发生了变化,其原因可能是产生了新的裂隙,也可能是裂隙贯通,这样就会同时导致裂隙的方向分布发生变化,裂隙场的熵会增大或者不变。如果某一单元的分形维数降低,可能是裂隙发生了闭合,裂隙的方向趋于同一方向,裂隙场系统的熵也会降低。当裂隙张开时,裂隙的长度占位空间不变,即分形维数不变,但是裂隙场的熵增加,裂隙趋于混乱。因此,可以用裂隙熵与分形维数相结合的方法来判断裂隙的状态,建立如表4-5的判断准则,其中“+”表示增加,“-”表示减小,“±”表示不变。
表4-5 采动覆岩裂隙演化时空状态判据

基于GIS,对覆岩裂隙的分形维数与裂隙熵的时空演化过程进行差异化计算,获得了采动覆岩裂隙判别参数的时空差异演化特征,如图4-34所示,在新裂隙产生区域,工作面推进过程中,裂隙场的分形维数和裂隙熵增加的区域均位于新裂隙产生的区域。工作面从120m推进至180m、从180m推进至240m、240m推进至300m、300m推进至340m以及340m推进至400m时,裂隙状态不变的区域,分形维数和裂隙熵不变的均在相同区域。工作面从240m推进至300m时,裂隙场部分裂隙状态发生变化的单元格见表4-6,结合表4-5以及图4-34可以判断采动覆岩裂隙过程中,各个位置的裂隙状态特征。
表4-6 部分裂隙分区状态
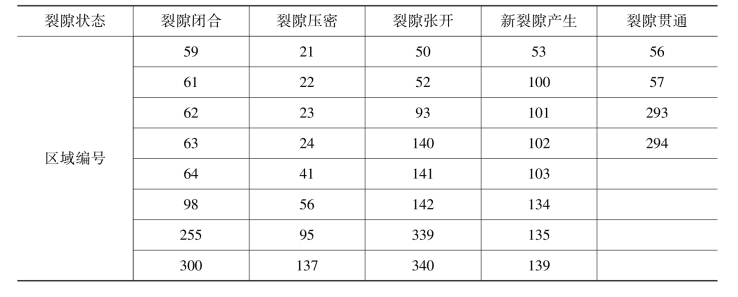
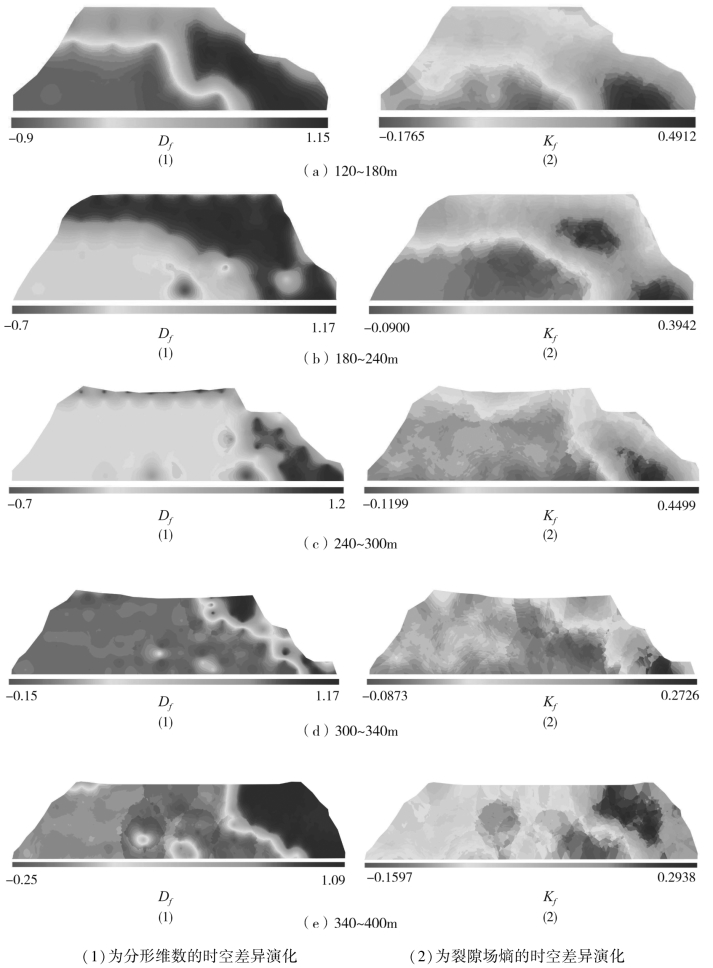
图4-34 采动覆岩裂隙场的时空差异演化特征
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




