图像二值化方法与实现

图像阈值分割因其直观、简单、运算速度快等特点，在图像分割应用中占有重要地位。阈值分割的方法也是对图像进行二值化常用的方法，图像二值化以后只有两种颜色，方便定量统计计算裂隙，图像二值化的关键步骤为图像的阈值分割，通过找到最合适的阈值，再经过计算灰度直方图中不同灰度值的二值化阈值，将灰度图像分离为裂隙和岩体成分。通过分析灰度图像的像素点，将大于阈值和背景的灰度值指定为0或1，小于阈值的裂隙元素的灰度值指定为1或0，如式（4-37）所示。

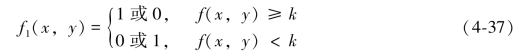
其中，f1（x，y）为二值化处理后图像的灰度值，k为阈值。

采用阈值分割方法对图像进行二值化，需要寻找最优阈值。寻找最合适阈值的方法有很多，许多为自动获取阈值的方法，常用的方法有迭代法、Otsu算法、自适应法、最大熵法等，其中迭代法比较简单且容易实现，是常用的阈值分割方法。

1）迭代法

迭代法首先是选取初始阈值，主要基于逼近思想，逐步计算出最优阈值，迭代法基本流程图如图4-6所示，为了计算方便，初始值往往选择灰度图像的平均值，由于迭代法是经过反复的迭代计算获得最优阈值，因此迭代法的计算量比较大，计算时间较长，特别是针对岩体裂隙图像，如果图像中存在假裂隙，经过去噪以后仍然存在颜色较深的部分，这主要是由于试验材料的特征所导致的。此时，使用迭代法会造成最优阈值计算误差较大。此方法适用于灰度图像直方图有明显波谷的图像阈值分割。

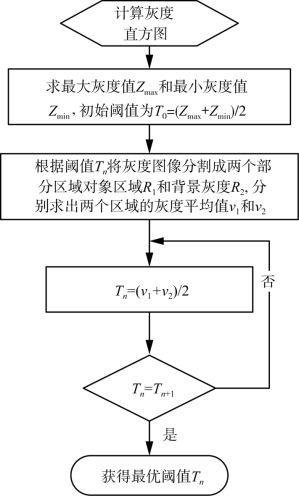
图4-6　迭代法阈值分割图像

2）Otsu算法

阈值化可以看作一个统计决策理论问题，其目标是最小化将像素分配给两个或多个组所产生的平均误差。众所周知，这个问题有一个合适的封闭形式的解决方案，称为贝叶斯决策函数。这个解决方案只基于两个参数：每个类的强度级别的概率密度函数和每个类在给定应用中发生的概率。但是，估计概率密度函数比较复杂，因此通常是对概率密度函数的形式作出可行的假设（例如假设它们是高斯函数）来简化问题。即使进行了简化，使用这些假设实现解决方案的过程也可能很复杂，而且并不总是很适合实时应用程序。

Otsu算法已经被证明优于其他阈值分割管道图像的方法。将图像直方图分为两组，具有一定的灰度值。当达到两组之间的最大方差时，灰度值是图像二值化所需的阈值，最佳阈值（T）通过以下方式获得：

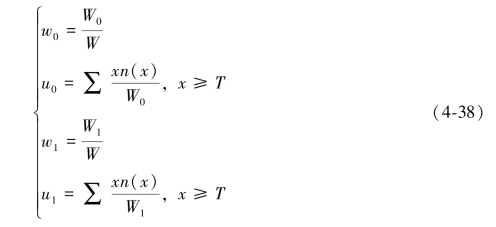
式中，W为图像像素数，T为目标和背景的分割阈值，n（x）为图像灰度值对应的像素数，u为图像的平均灰度值，两组之间的方差记录为σ2。当x≥T时，目标像素数W0与图像的比值为w0，目标像素的平均灰度为u0。当x＜T时，背景像素数W1与图像的比值为w1，背景像素的平均灰度值为u1。

图像u的平均灰度级可以用以下公式计算：

(www.xing528.com)

具有最佳阈值T的前景和背景之间的方差可通过以下方法计算：

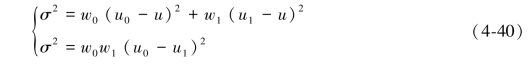
由上式可知，最佳阈值T由σ2的最大值来决定。

3）最大熵法

正如前文所述，在图像处理中，从图像中提取目标元素最常用的方法是迭代法。特别是对于岩体裂隙图像，如果裂隙与背景（岩体）有明显的区别，裂隙图像转换为灰度图像后，获得的灰度直方图将是双峰的，分割阈值可以在谷底选择，适合采用简单的迭代法获得图像的阈值。然而，图像中的噪声是不可避免的，虽然经过多种滤波处理，但依然无法达到理想化的状态，特别是岩体采动裂隙具有复杂性和变化性的特征，灰度直方图并不总是双峰的。因此，解决这一问题迭代法并不适应。多年来，人们提出了许多方法来克服这一困难，大多数是将问题试图简化为双峰情况。还有一些学者试图通过定义改进的图像直方图来简化阈值的选择。当然，还有一些其他的方法，如Otsu算法。

而数字图像是由有限的离散元素组成的，因此根据信息熵理论，图像具有熵，因此可以利用图像熵来对灰度图像进行阈值分割，该方法最早是由Kapur，Sahoo和Wong提出的。首先设定一个阈值v（0≤v＜n－1），采用此阈值将图像分割为两个区域A和B，其中A和B可以定义为：

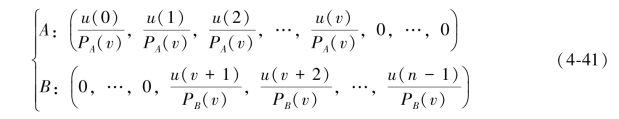
式中，PA（v）表示v阈值分割图像的背景像素累计概率；PB（v）表示v阈值分割图像的前景像素累计概率，计算如下：

图像的背景与前景所对应的熵计算可以定义为：

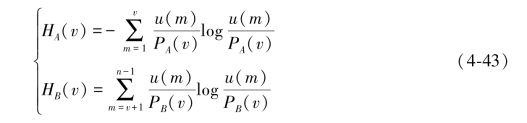
因此可以获得图像的总熵值H（v）：

然后对图像进行i次分割，并计算其每个熵值Hi（v），最终获得H max（v），此时H max（v）对应的阈值就为图像分割的最优阈值。