1)根据测度关系计算分形维数
如果分形具有非整数维数,周长与面积关系的分形计算模型与测度关系模型是相似的,此首先由Mandelbrot提出,可以根据其定义来求解分形维数,定义一个规则的立方体,其长度为L,面积为S,体积为V。如果改变其一个变量,例如L,当L增加到原来的2倍,则其面积就增加到原来的4倍,其体积则增加到原来的8倍。
![]()
由此当L扩大多少倍,其S1/2与V1/3也同样扩大多少倍,因此可定义一具有D维度的量维Y,则
![]()
因此,可以据此计算分形对象的维数。同样的对于一个二维图形,其周长为L,面积为S,则其周长与面积的关系可以定义为:
![]()
其中,L为图形的周长,S为图形的面积,对图形的周边曲线进行测量,当尺子减小到一定时,其面积基本稳定在一个固定值,因此可定义为:

其中,D为图形的边界分形维数,当尺子足够小的时候可以转换为:
![]()
其中,c为比例系数,此种测量方法经常被用于测量物体结构面。基于此,武生智等[182]对砂粒粗糙度及其粒径分布进行了研究,并提出了砂粒表面粗糙度分形维数测度的计算公式:
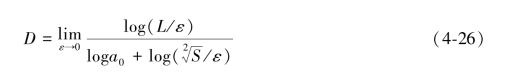
其中,a0为形状因子,S为曲线的欧氏面积,L为曲线的欧氏长度,ε为标度。
2)根据分布函数求分形维数
定义r为测度物体的径长,Nr是所有观察尺度为r的物体的总数,把直径大于r的物体出现的概率定义为P(r),其分布的密度概率为P(s),则有:
![]()
当测度变化而其分布不变时,则必须满足:
![]()
因此可得:
![]()
换个方式来说[183],对于直径大于r的,则物体的分形维数D与r的关系可以表示为:(https://www.xing528.com)
![]()
3)根据波谱密度求分维
此方法又被称为PSD(Particle Size Distribution)法,在对随空间或时间变化的变量进行观测时,可以得到空间序列或者时间序列的变化频谱[184-187]。对于频谱来说,改变观察尺度相当于改变其截止频率fc。如果此具有分形特征,即使截止频率改变了,其频谱图形是不会变的。具有此种性质的频谱或波谱只能用如下分布来定义:
![]()
而β与分形维数D满足:β=5-2D。而如果是在曲面的情况下,即二维时:β=57-2D。Tyler和Wheatcraft对土壤颗粒进行了PSD分析[186-187],得到N(r>R)∝R-D,其中,N(r>R)为颗粒尺寸大于或等于R的颗粒数目,D为频谱分形维数。
4)改变标尺法求维数
此方法主要通过用基本规则分割具有分形性质的图形,扩展到二维或三维,就是把平面或者空间分割成尺寸r足够小的基本图形,然后计算需要测度的图形所包含的基本图形个数N(r),由于N(r)∝r-D的关系,此方法经常被用于分形维数的计算,特别是随着计算机的发展,此方法更易通过计算机来实现大量数据的精确快速计算。冯夏庭等[188]通过使用不同的尺子长度r去测量岩石的节理长度,并获得了岩石节理粗糙系数[189](Joint Roughness Coefficients)与节理分形维数的关系:

式中,JRC为岩石节理粗糙系数,N为节理长度,D为分形维数。
温世游等[190]基于损伤力学与分形理论,推导了岩体损伤的本构模型,并定义了损伤变量:
![]()
式中,m为裂隙的分形维数,S为裂隙的面积,a为单位裂隙面积。
随着计算机的发展,GIS作为一门学科,其具有强大的空间数据处理功能,即能对宏观的数据进行处理,也可以对微观的数据进行处理,能够实现在不同的规模上进行数据图形的空间处理。王宝军、施斌等[192]通过图像处理技术与GIS对黏性土的形态特征基于测度关系进行了三维的分形分析。
标尺法不仅适用于点分布和曲线分布,还可以用来对采动裂隙发育,特别是当覆岩发生垮落断裂时,形成的具有大量分叉的信息,因此可以通过此方法来计算获得其计盒维数。计盒维数的计算可以通过标尺法来实现,作为目前应用比较广泛的分形维数表示方法,其计算可以有效地与计算机结合起来。因此可以与GIS相关软件结合起来进行分形维数的快速计算,GIS可以将图形处理成为栅格数据,栅格数据不但具有空间位置信息,还具有空间属性特征。应用GIS计算来实现分形维数的计算,以下举例说明。如图4-2所示,将图形转换为不同栅格单元大小的栅格图层,然后绘制栅格单元大小与栅格数目的双对数图,如图4-3所示,图中纵横坐标分别为N(r)和1/r的原始数据,并对其取对数,用此图也可表示分形维数的计算流程,图中直线的斜率即为此图形的分形维数,D=1.51。
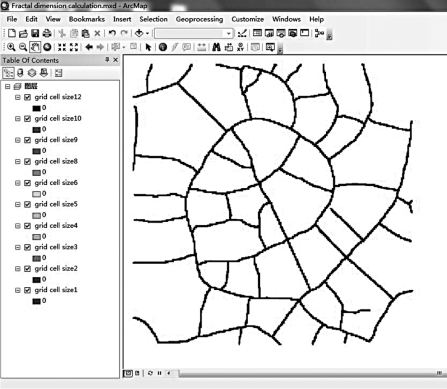
图4-2 不同栅格大小的栅格图层
表4-1 划分的网格数目

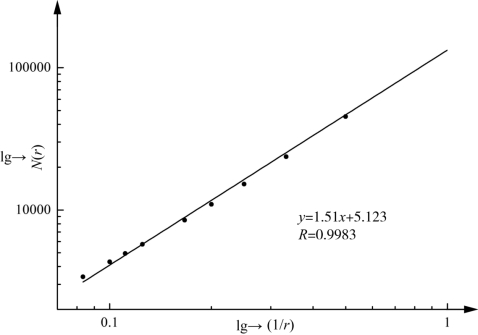
图4-3 分形维数计算过程图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




