岩体采动裂隙与突水危险性研究：分维及决策模型

分维是定量地描述分形系统的一个参数，假设测量一单位线段，如果选择的尺子长度a＝1，则测量次数N＝1，得出的长度L＝N·a＝1；当a＝1/2时，则N＝2，仍有L＝1，类似地不断缩小尺子长度，则测量次数就会越来越大，但是总长度L不会改变[171-177]。将不同测量尺度和测量长度在同一坐标系中绘制双对数图像，会得到一个水平直线，该直线的斜率等于0。分形理论中的一个经典案例——海岸线长度测量，如图4-1所示。但选用较大的尺子a去测量时，许多比较小的位置将会被忽略，如峡谷等，如果尺子变小后，许多更小的位置也会被忽略掉。因此不断地缩小尺子a，则测量的长度可以近似地表示为：

图4-1　挪威海岸线

其中，D为曲线的分维，一般地，对于分形曲线D＞1，则

其中，曲线的长度随着尺子趋于0而趋于∞。

为了对分形进行表征，许多不同的维数被提出，主要包括容量维、信息维、关联维等常见的几种[178]。

1）容量维

设一个直径为a的小球，当其被覆盖后的最小数目为N（a），这个集合的容量维数可以通过以下计算：

容量维基本上与Hausdorff维数类似，主要是由Kolmogorov推导的，基本上就是Hausdorff维数的广义定义，所以在许多实际问题中，Hausdorff维数与容量维数的差别是可以忽略的。

2）信息维

信息维的提出是为了区别每个球覆盖点数的多少，这个在上述容量维中没有被考虑，因此信息维可以被定义为：

其中，在第i个球中出现的概率可以用Pi表示。

3）相似维数

众所周知，一直线段的维数是1，设一直线段的长度为X，并分成N＝b个等长的小线段，每一小段是整个直线的比例缩小，这个比例称为相似比r，可以得到r＝1/b＝1/N。如果是二维问题，可以分成N＝b2个小方块，这些小方块相似整个二维平面，可以定义为：

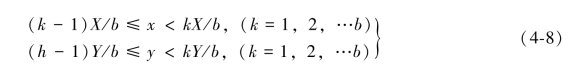
其相似比为：

对于三维的六面体，类似地，可获得相似比：

类推之，对于Ds维柱体，其相似比为：(www.xing528.com)

因此可得：

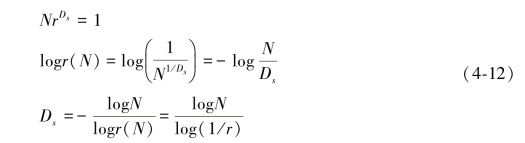
其中Ds就为相似维数。

4）关联维数

关联维数是根据关联函数计算的分形维数，可以在实验中直接测定，应用比较广泛，定义某变量在空间的分布在X位置的密度为ρ（y），则关联函数C（ε）记为：

如果变量在空间的分布是均匀的，各个方向均相同，可以用两点的距离来表示其关联函数。Grassberger与Procaccia在1983年提出关联维数的定义[179-180]：

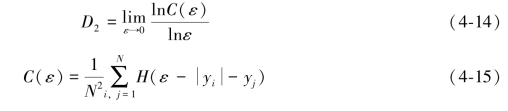
5）广义维数

广义维数是由Hentschel与Procaccia提出的，可定义为[181]：

式中，

Sm（ε）是m阶Rényi信息，Dm为m阶的广义维数，又可称为Rényi的信息维数，其中m为整数。当m＝2时，基于洛必达法则，可得：

当Dm＝D2，广义维数与关联维数相等。

6）计盒维数

计盒维数DB是被大家广泛采用的一种方法，由于其可以比较容易地利用计算机等进行计算，定义B为一个有限集合，N（r）是直径最大的r能够覆盖B集的最少个数，则其可以定义如下：

当，则其就为B的盒子维数，定义为：

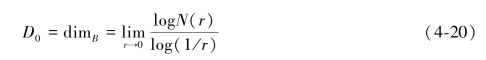
当公式（4-16）与式（4-17）中m取0时，广义维数与盒子维数相等。