1)采动覆岩应力演化特征
模型开采过程中,每完成一个开采步距后,持续一定的时间再进行下一步开采,对其持续时间过程中的数据进行采集,通过对采集的应力数据进行处理。由于每一步采动后,应力将重新逐渐达到平衡。我们对采集的数据进行处理时,主要对采动过程中的垂直应力进行分析,如图3-6所示,为模型开采10cm(实际工程开采20m后)时,A1点在第一个开采时间周期内应力监测的数据,其应力熵为3.55。

图3-6 开采10cm时A1点应力变化

图3-7 采动过程中第1列测点应力演化图
如图3-7、图3-9和图3-11所示,距离煤层底板47.7cm以上测点受到采动影响变化不大,因此其应力熵变化也不会明显,我们对其余测点应力时间序列的应力熵进行计算,获得各个测点的应力熵变化图,如图3-8、图3-10和图3-12所示。在开采初期,模型一直处在稳定状态,随着工作面向前推进,形成采空区,当工作面开采20m(模型采动10cm)时,工作面覆岩上方覆岩应力变化较小,分布比较均匀,对比图3-9,此时未影响到工作面前方。


图3-8 采动过程中第1列测点应力熵

图3-9 采动过程中第2列测点应力演化图
距离煤层底板23m(模型11.5cm)的A1测点,工作面开采40m到60m过程中,采空区上方23m处的测点卸压,表现为覆岩应力发生了重新分布,而应力熵提前发生了变化。A2测点的应力熵滞后变化,即当应力(卸载)突然减小时应力熵会提前发生突变,当应力升高时,应力熵的突变滞后。而A2应力一直在增加,覆岩中此点能量一直在增加,当其能量超过岩体的极限强度时,覆岩将会发生破断、垮落,最终此位置的应力释放。而在此过程中,采动应力扰动并未达到A3测点,即在煤层底板以上67.8m(模型33.9cm)处。而测点A4距离煤层底板95.4m,直到工作面推进160m处,基本未受到扰动。
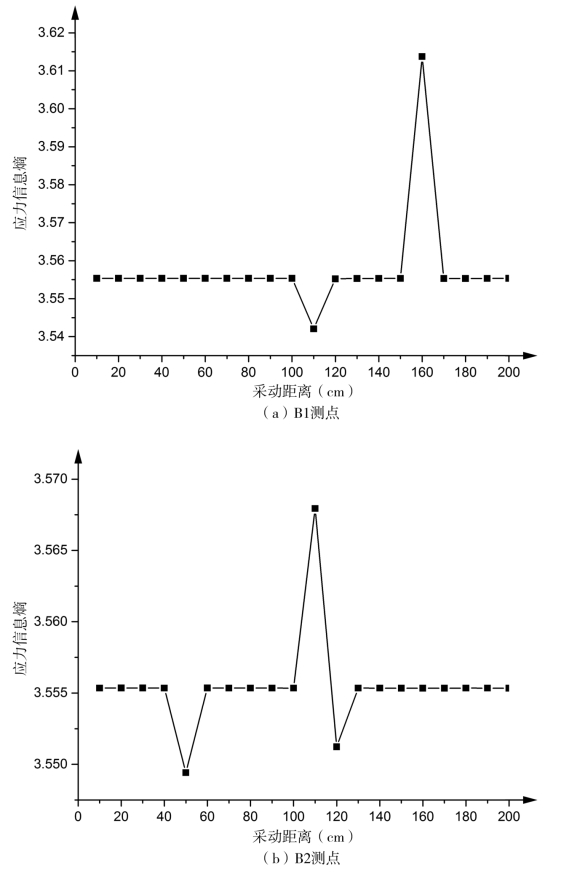

图3-10 采动过程中第2列测线应力熵
 (https://www.xing528.com)
(https://www.xing528.com)
图3-11 采动过程中第3列测点应力演化
从开采120m开始,A1测点的应力逐渐开始恢复,采动过程中第2列测点应力的变化反映了工作面正常回采过程中应力的变化,工作面前方一定范围内的未采动岩体应力有一升高区,并且此区域伴随着工作面的正常回采逐渐变化,采空区下位岩层处于低应力状态。而随着工作面的正常开采,工作面前方的覆岩中的垂直应力呈现周期性变化,而每次应力突变时,都伴随着应力熵的突变,如图3-8、图3-10、图3-12所示。在顶板破坏前,附近测点的应力数值一直在增大时,覆岩中一直在蓄积能量,当顶板发生破坏后,覆岩中蓄积的能量产生耗散,此处的应力开始卸载,特别是进入采空区后,其应力由于受到破坏岩体的作用,以及覆岩的压实运动,应力开始恢复,但有些部分无法恢复到初始应力值。而在工作面前后未采煤岩体和上方一定高度的岩层均有高应力的存在,这充分证明了采场围岩有动态应力拱的存在,其主要承担并传递上覆岩体的荷载和压力。


图3-12 采动过程中第3列测点应力熵
2)采动裂隙岩体应力时空可视化
由于采动覆岩应力变化的历时性,可以对采动覆岩应力变化进行时空可视化分析,表3-6为2018年1月19日0点与17:30的同一测点A1的数据,列举了部分采动覆岩应力监测点应力值,其中应力值为时间段内平均值。
表3-6 覆岩应力监测平均值(前35小时)

基于GIS,以测点位置为平面二维坐标,以时间t为第三维度坐标,建立采动覆岩应力时空立方模型,在3D场景下显示,并对结果进行处理,未有监测点不参与计算,并附上坐标如图3-13所示。对采动覆岩应力时空模型进行Man-Kendall趋势分析,主要分析随着时间的推移,应力总体的变化特征,总观测数300个,总观测值4200个,Z得分为-1.86,表明随着时间的推移采动覆岩应力整体上具有显著性减小的趋势。

图3-13 采动覆岩应力时空立方模型
为了研究在工作面推进过程中,每步开采应力重新平衡的过程中,即每步开采的时间周期内,覆岩应力的时空演化,以开采距离和监测时间作为两个维度,而不同测点作为第三维坐标,此时主要考虑导水裂隙带内及其附近的测点,用不同的颜色表示应力值,由此获得如图3-14所示的时空立方体,描述每步开采达到应力平衡周期内的覆岩应力时空演化特征。对此采动覆岩应力时空模型进行Man-Kendall趋势分析,主要分析随着时间的推移,应力在总体上的变化特征,180个具有估计观测值的位置,2520个已估计的全部观测值,Z得分为-2.63,表明导水裂隙带内覆岩应力随着时间的推移采动覆岩应力整体上具有显著性减小的趋势,且比整个工作面覆岩应力的下降趋势更加明显。

图3-14 采动覆岩应力时空立方体
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




