【摘要】:H.B.Man与M.G.Kendall提出了一种非参数统计检验方法,即Man-Kendall趋势分析法[159],该方法作为时空统计分析的有效方法,对样本分布特征无要求、受到异常点值的干扰较小,常常被用于时间序列的趋势检验。并且Getis-Ord Gi*热点分析统计方法的检测时间序列变化趋势基础也是Man-Kendall趋势分析方法[160]。
H.B.Man与M.G.Kendall提出了一种非参数统计检验方法,即Man-Kendall趋势分析法[159],该方法作为时空统计分析的有效方法,对样本分布特征无要求、受到异常点值的干扰较小,常常被用于时间序列的趋势检验。并且Getis-Ord Gi*热点分析统计方法的检测时间序列变化趋势基础也是Man-Kendall趋势分析方法[160]。
定义一个时间序列Y,假设其样本个数为n,则Man-Kendall中的备选假设和原假设如下:
原假设A:时间序列Y是相互独立,且具有随机概率,分布相同的样本;
备选假设B:对于任意i,j≤n,且i≠j,Yi与Yj的分布不同。
构造检验统计量T:

对于n≥10,统计量T近似服从正态分布,可知其均值为0,其方差为:
![]()
其标准化检验统计量Z为:(https://www.xing528.com)

对于趋势检验,假设显著水平为a,则置信度p=1-a,对于如下成立:
![]()
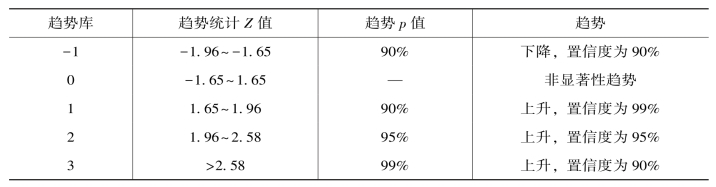
原假设被排除,可知此序列有明显的变化趋势。因此在标准化检验统计中得到Z得分,可通过在得分判断序列的趋势特征,对于大于0的值,当其值越高时序列的上升趋势越明显,当其小于0时,越小下降序列越明显,其趋势显著性分级见表3-1[160-161]。
表3-1 趋势显著性分级

续表
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




