建筑工程制图：平面立体正轴投影画法

1.坐标法

根据轴测投影的规律,将形体上的各顶点按直角坐标值移置到轴测坐标系中,定出各点、线、面的轴测投影,从而画出整个形体的轴测图,这种作图方法称为坐标法。

【例6-1】　根据三棱锥的正投影图[图6-5 (a)],试用坐标法画出其正等轴测图。

分析作图:作图步骤如图6-5所示。

图6-5　用坐标法作三棱锥的正等测图

(a)在三棱锥的投影图上确定坐标系,并量出各点的坐标值;(b)画轴测轴,确定底面各顶点和锥顶在X1O1Y1 面上的次投影;(c)根据棱锥的高度定出锥顶;(d)连接各顶点即完成作图

2.叠加法

叠加法是将形体分解为若干基本形体,依次将各个基本形体进行准确定位后叠加在一起,形成整个形体的轴测图。对于组合形的几何体,一般采用叠加法比较恰当。

【例6-2】　根据柱基础的正投影图[图6-6(a)],试用叠加法画出其正等轴测图。

分析作图:

从图6-6(a)的正投影中可以看出,这是由三个四棱柱上下叠加而成的柱基础,其作图步骤如图6-6所示。

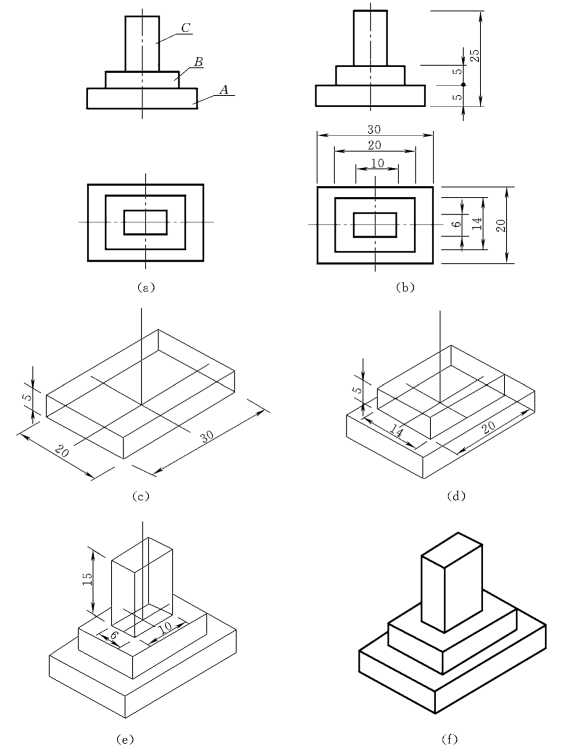
图6-6　用叠加法作柱基础的正等测图

(a)柱基础的分解;(b)确定各四棱柱的大小尺寸;(c)画出轴测轴,作出底部四棱柱A 的轴测图;(d)将轴测坐标原点上移至四棱柱A 的上表面中心位置,作四棱柱B 的轴测图;(e)用同样的方法作出顶部四棱柱C的轴测图;(f)区分可见性,加深图线,即得柱基础的正等轴测图

3.切割法(www.xing528.com)

有些形体可以看成是由简单形体经过若干次切割而成。画图时,可先画出完整的简单形体,再进行切割,画出形体的轴测图。它适用于具有切口、开槽的简单形体的表达。

【例6-3】　根据形体的正投影图[图6-7(a)],试用切割法画出其正等轴测图。

分析作图:

从图6-7(a)的正投影中可知,它是由一个长方体切去一个三棱柱和一个四棱柱所形成的,这种形体适用切割法作图,其作图步骤如图6-7所示。

图6-7　用切割法作形体的正等测图

(a)形体的正投影图;(b)确定长方体尺寸和各切割部分的尺寸;(c)作出长方体的轴测图;(d)切除三棱柱;(e)切除四棱柱;(f)区分可见性,加深图线,即得轴测图

4.综合法

当形体的形状由若干部分组成,且每个部分上都有切口、开槽等结构时,综合使用叠加法和切割法,从而使作图简单化,这种画轴测图的方法称为综合法。

【例6-4】　根据台阶的正投影图[图6-8(a)],画出其正等轴测图。

分析作图:

从图6-8(a)的正投影中可知,台阶由左右牵边和中间三级踏步构成。两侧牵边各被切去一个三棱柱,其作图步骤如图6-8所示。

图6-8　台阶的正等测图画法

(a)已知台阶的正投影图;(b)定正等轴测轴;(c)作长方体箱子;(d)作台阶左右牵边;(e)作台阶左端面;(f)完成全图