建筑工程制图中的旋转法分类及应用

旋转法和换面法不同,它不需设立新投影面,而是保持投影面不动,使空间几何元素绕垂直于某投影面的轴线旋转到与另一投影面处于所需的特殊位置,如图3-20(b)所示。

旋转法按所选旋转位置的不同可分为两大类;绕投影面垂直线旋转法和绕投影面平行线旋转法(只适宜于解决有关同一平面内的问题)。现将空间几何元素绕垂直线的旋转法概述如下。

(一)旋转法的基本规则

(1)旋转轴垂直于投影面,并按解题要求可选择以正垂线为旋转轴来旋转空间几何要素。为简化作图过程可使旋转轴通过几何要素。

(2)旋转时几何要素间必须遵守绕同一旋转轴、按同一方向及旋转同一角度的“三同”规则,将其旋转到有利于解决定位和度量的位置。

(3)旋转空间几何要素时,点、线、面的投影规律及作图规律仍适用。

(二)旋转的基本规律及其作图

(1)点绕垂直于投影面的轴线旋转时,它的旋转轨迹在该投影面上投影为一圆,而在另一投影面上的投影为平行于投影轴的直线(点旋转轨迹所在的平面为投影面的平行面),如图3-30所示。

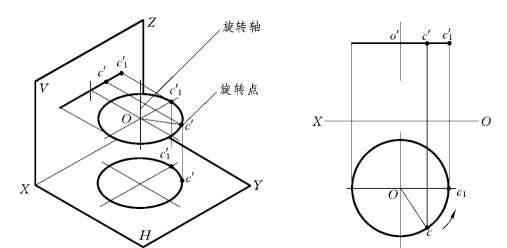
图3-30　点绕垂直于投影面的轴线旋转

(2)旋转直线时,把确定直线空间位置的两点按照“三同”规则旋转。

(3)直线绕铅垂轴旋转时,其水平投影的长度不变,对H 面的倾角α 不变;直线绕正垂轴旋转时,其正面投影的长度不变,对V 面的倾角β 也不变。

(4)若将一般位置直线旋转为投影面平行线,可使旋转轴(正垂轴或铅垂轴)过直线两端点中的一端,来旋转直线成为投影面平行线。只需一次旋转就能实现。

(5)把投影面平行线旋转成投影面平行线,若直线为正平线其旋转轴应为正垂轴;若直线为水平线其旋转轴就应是铅垂轴。只需旋转一次就能实现。

(6)把一般位置直线旋转为投影面垂直线,首先应将一般位置直线旋转为投影面平行线,然后再将这一投影面平行线旋转为垂直线。即把一般位置直线旋转成投影面垂直线,须经二次旋转(先平行后垂直)才能实现。(www.xing528.com)

旋转法用来求线段实长、平面的实形以及它们和投影面的倾角等问题,作图较简便。

(三)常用的旋转法应用示例

1.将一般位置直线旋转成正平线

【例3-10】　图3-31是将一般位置直线AB 旋转成正平线的作图方法。

分析:首先必须选择取一个合适的旋转轴。由于线段绕垂直于正面的轴旋转时β角不变,因此不可能绕这样的轴将直线AB 旋转成β=0的正平线,所以应选垂直于水平面的轴,而且为了作图简便,可以使旋转轴通过线段AB 的端点A [图3-31(a)],这样A点在旋转时位置不变,只要旋转一个B 点。要使直线AB 成为正平线,必须在水平投影上将b点绕旋转轴旋转到使b1a∥OX,然后按点的投影规律求得b′1,再用直线连接ab1和a′b′1 即得AB 旋转成正平线的投影,它的正面投影反映了该线段的实长及对水平面的倾角α,图3-31(b)所示为作图方法。

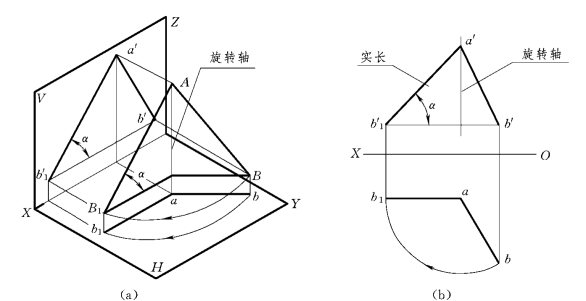
图3-31　一般位置直线旋转成正平线

将一般位置直线旋转为水平线方法与上类似。

2.将平行线(正平线)旋转成垂线(铅垂线)

【例3-11】　图3-32是正平线旋转成铅垂线的作图方法。

分析:要使正平线旋转成铅垂线,应选择垂直于正面的旋转轴,为了作图方便可使旋转轴通过直线的一个端点B,然后将A 点绕轴旋转到使直线处于铅垂位置,具体作图如图3-32所示。将水平线旋转为正垂线方法与此类似。

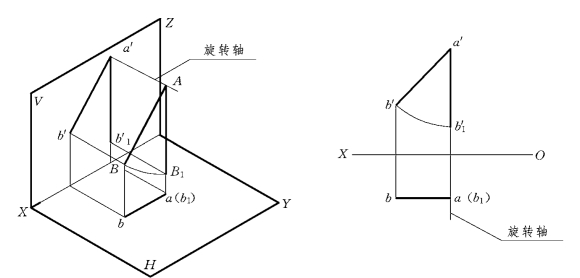
图3-32　正平线旋转成铅垂线

从上述例子可以看出,直线绕垂直于某一投影面的轴旋转时,直线对该投影面的倾角不变,因此,要使一般位置直线旋转成投影面垂直线,必须旋转两次,即是先将它旋转成某投影面的平行线,然后再将它旋转成投影面垂直线。这与换面法中换两次面的情况是相似的。