建筑工程制图：点的投影规律

从图3-1可知,点A 的V 面投影和H 面投影共同反映点A 的x 坐标;点的V 面投影和W 面投影共同反映点A 的z 坐标;点的H 投影和W 投影共同反映点A 的y 坐标。由此可得出点的三面投影规律:

点的V 面投影和H 面投影的连线垂直于OX 轴,即aa′⊥OX;(长对正);

点的V 面投影和W 面投影的连线垂直于OZ 轴,即a′a″⊥OZ(高平齐);

点的H 面投影至OX 轴的距离等于点的W 投影至OZ 轴的距离,即aax=a″az,同时aayh⊥OYH,a″ayw ⊥OYW(宽相等)。

为了表示点的水平投影到OX 轴的距离等于侧面投影到OZ 轴的距离,即:aax=a″az,点的水平投影和侧面投影的连线相交于自点O 所作的45°角平分线,如图3-1(c)所示。

【例3-1】　已知点A 和点B 的两投影,如图3-2(a)所示,分别求其第三投影,并求出点A 的坐标。

图3-2　已知点的两面投影求第三投影

解:(1)如图3-2(b)所示,根据点的投影特性,可分别作出a和b″。(www.xing528.com)

(2)如图3-2(c)所示,分别量取a′az、aax、a′ax 的长度为10、4、12,可得出点A 的坐标(10,4,12)。

【例3-2】　已知空间点A(30,10,20),试作点A 的三面投影。

解:根据点投影与坐标的关系,可以由点的已知坐标定出各面投影的位置。H 投影可由x=30,y=10作出;V 投影可由x=30,z=20 作出;W 投影可由y=10,z=20作出。

作图过程如下:

(1)作相互垂直的投影轴,分别在各投影轴上截取x=30,y=10,z=20,如图3-3(a)所示。

(2)由各坐标点作所在投影轴的垂线,分别相交于a、a′和a″三点,即得点A 的三面投影,如图3-3(b)所示。

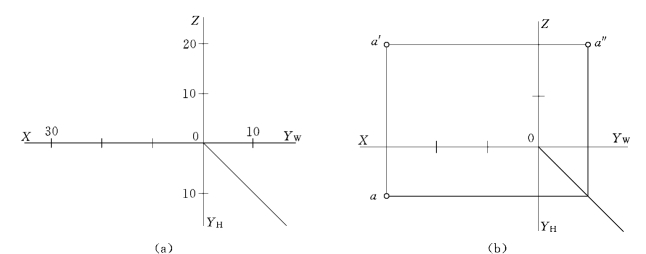
图3-3　根据点的坐标作点的三面投影