基于范数灰关联度的多目标系统方法

对于多目标决策优化问题，可作_出如下一般形式的数学描述：

目标函数：

约束条件：

gi(x)≤0(i=1,2,…,m)xj≥0(j=1,2,…,n)

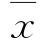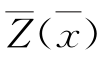式中：xj是第j个决策变量；是以n个决策变量为分量的决策向量；是各个目标功能指标的函数值；是对于k个目标的k维目标函数向量。

4.3.1　多目标系统协调优化方法的分析

关于多目标系统协调优化解的讨论，采用了向量优化（vector optimization）的方法。为阐述方便，首先引进序（order）的概念。

设

规定：

类似地可以规定≥和＞的含义。有了上述规定，可以引进向量值优化问题解的概念。

设标准的优化问题的表达式如下：

当P=1时，即为单目标问题。对于单目标问题，可以求出优化解。而对于多目标规划问题有如下解的概念：假设存在x0∈Rn为满足约束条件的一个点，并且对于所有满足约束条件的点x∈Rn有：f（x0）≤f（x）。则称x0为多目标问题的绝对最优解。由于多目标问题的复杂性，要想找到绝对最优解是比较困难的，有时这种绝对最优解根本不存在，只能在某种意义下找出非劣解，也称Pareto最优解。所谓非劣解x0，就是不存在约束集合中的x使得f（x）≤f（x0）。

尽管多目标优化问题有各种意义下的最优解，但在应用中，最重要的还是非劣解，关于求非劣解的最基本的方法是评价函数法。所谓评价函数法，是利用多目标问题的目标函数f（x），构造一个复合函数，然后在约束集合D上极小化，φ的构造必须满足一定的条件，使得的最优解就是多目标问题的非劣解。

4.3.2　构造评价函数的方法

在系统优化时经常用到的几种构造评价函数的方法主要有：理想点法、线性加权和法和极大极小法。

（1）理想点法。在上面所讲的多目标模型中，先求解p个单目标问题

设其最优值为f*j，称f*=（f*1，…，f*p）为值域中的一个理想点，因为一般很难达到它。这样，就期望在某种度量下，寻求距f*最近的f作为近似值。一种最直接的想法是构造评价函数：

然后极小化，即求解

并将它的最优解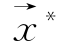作为多目标优化模型在某种意义下的最优解。

（2）线性加权和法。在具有多个指标的问题中，人们总希望对那些相对重要的指标给予较大的权系数。基于这种现实，自然如下构造评价函数，令

称之为权向量集。

令

再求解

而将它的最优解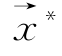作为多目标优化模型在该意义下的最优解。(www.xing528.com)

（3）极大极小法（Minimax Method）。在决策时，采取保守策略是稳妥的。即在最坏的情况下，寻求最好的结果，按照这种想法，可以构造如下的评价函数

然后求解

并将它的最优解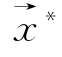作为多目标优化模型的最优解。

除以上3种评价函数外，还有很多其他形式，这里不再详述。在实际应用中通常采用线性加权和法来构造评价函数，从而求解出多目标协调优化模型的非劣解。在使用线性加权和法来构造评价函数的过程中，必然要涉及到权重的确定，下面就介绍权重的求解方法。

4.3.3　基于范数灰关联度的权重计算方法

权重是以某种数量形式对比、权衡被评价事物总体中诸因素相对重要程度的量值。它既是决策者的主观评价，又是指标本质的物理属性的客观反映，是主客观综合度量的结果。权重主要决定于两个方面：第一，指标本身在决策中的作用和指标价值的可靠程度；第二，决策者对该指标的重视程度。指标权重的合理与否在很大程度上影响综合评价的正确性和科学性。为了使评价结果减少人为主观因素的影响，更多地反映事物的本质，本文介绍一种基于范数灰关联度的方法求解权重。

基于范数灰关联度确定指标权重的综合评价法以灰关联分析为基础，充分利用现有的指标值，通过考察各评价对象指标值与参考值的差异，以量化后的差异为基数，最后对评价对象进行排名，是客观的综合评价方法。它的实质就是整体比较，是有参考系、有测度的比较。

（1）指标数据规范化。根据指标的性质不同，可将指标分为效益型、成本型和区间型。效益型指标是指指标取值越大越好，成本型是指指标取值越小越好，而区间型指指标取值越接近某个固定区间{q1j，q2j}。设m为评价对象数，n为指标个数，xij为第i个评价对象的第j个指标值，并记zij为规范化后的指标值，Jk（k=1，2，3）分别为效益型、成本型、区间型指标。则

（2）确定参考序列x0。效益型指标应在指标取值中取最大数为该指标的参考数。

（3）计算各评价对象与参考序列的差值绝对值。

Δih=|zih-x0h|(i=1,2,…,m;h=1,2,…,n)

可见，差值绝对值越小表示该对象离参考序列越近。这些差值组成了一个m×n的矩阵X。

（4）计算指标权重。考虑指标j对指标体系中其余指标k（k≠j）的影响程度，如果某个指标对其他指标的影响程度越大，说明该指标在系统中包含的信息量越大；反之，则说明该指标在系统中包含的信息量越小。对指标j，以其他指标k的指标值为参考序列，以指标j的指标值为比较序列，求得指标j相对于其他指标k的灰关联度，最后得到指标j的群灰关联度。ri（j，k）为指标j对于指标k的第i个灰关联系数，

yk（g）和yj（g）分别表示对应于指标k和指标j的第g个指标值；ζ为分辨系数，在最少信息原理下，ζ=0.5。按传统灰关联度求取方法，指标j对于指标k的灰关联度为

可看出某指标与其他指标的灰关联度是基于均值思想的灰关联度，均值思想的灰关联度可能造成对关联因素个性信息的湮没，进而产生最终整体接近性的序关系的误判，这与灰色系统补充信息转化性质的目标相背离；范数灰关联度是在不改变关联系数的情况下，对个性信息的再挖掘，即是一个信息的补充过程。范数灰关联度具有较大的优越性，它在灰关联分析过程中能进一步分析结果的正确性。

设ηi=ri（j，k）表示第j个指标对应于第k个指标的第i个关联系数。

为关联系数理想列，

为关联系数负理想列，i=1，2，…，m；k=1，2，…，n；k≠j。η+刻画的是距参考序列距离最近的比较序列。而η-刻画的是距参考序列距离最远的比较序列。第j个指标的关联系数列Yj（k=1，2，…，n；k≠j）的2个范数定义为

其中，称d+j为第j个指标的近距，称d-j为第j个指标的远距。在确定关联度时，近距越小远距越大的话则比较序列的关联性越强，指标j对应于其他指标k的范数灰关联度定义为

求得指标j对应于其他各指标k的范数灰关联度后，即可得指标j的群灰关联度εk=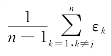。最后得到各指标的权重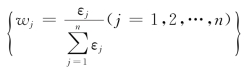

通过如上基于范数灰关联度的权重计算就可以把一个多目标系统协调优化方法的多目标系统问题转化为单目标问题，即上述多目标问题可以转化为下述单目标问题。

目标函数：

通过这样的转化，多目标系统协调优化的方法就具有了现实的可操作性，这就是基于范数灰关联度多目标系统协调优化方法的主要思想。本文就是利用基于范数灰关联度多目标系统协调优化方法来建立节水型社会建设与经济社会跨越式发展的协调模型。