2.2.1 各评价指标的权重
在确定了各层次的隶属关系和评价指标之后,各指标以及各主体层的权重确定过程和方法是评价模型的核心。权重的确定直接影响评价的结果。过去权重往往由专家主观确定,因人而异。现在常用的一个方法是先构造两两比较判断矩阵,指标权重由各指标之间的两两比较关系判断矩阵计算得到。
(1)构造两两比较判断矩阵。构造两两比较判断矩阵是对同一层次指标,进行两两比较,其比较结果以1~5标度值表示,各级标度的含义见表9-16。标度值由有关专家确定,比较容易取得一致,因人而异成分较小。
表9-16 1~5标度的含意

根据节水评价体系各指标之间关系的相对重要性,构造两两比较判断矩阵如表9-17~表9-42。(由于水资源条件和经济发展程度等不同,各地各指标之间关系的相对重要性也不同,因此需要按不同类型区分别设置两两比较判断矩阵表)
表9-17 主体层两两比较判断矩阵(经济发达,缺水地区)

表9-18 主体层两两比较判断矩阵(经济发达,不缺水地区)

表9-19 主体层两两比较判断矩阵(经济欠发达,缺水地区)

表9-20 主体层两两比较判断矩阵(经济欠发达,不缺水地区)

表9-21 综合评价指标两两比较判断矩阵(经济发达,缺水地区)

表9-22 综合评价指标两两比较判断矩阵(经济发达,不缺水地区)

表9-23 综合评价指标两两比较判断矩阵(经济欠发达,缺水地区)

表9-24 综合评价指标两两比较判断矩阵(经济欠发达,不缺水地区)

表9-25 农业节水指标两两比较判断矩阵(经济发达,缺水地区)

表9-26 农业节水指标两两比较判断矩阵(经济发达,不缺水地区)

表9-27 农业节水指标两两比较判断矩阵(经济欠发达,缺水地区)

表9-28 农业节水指标两两比较判断矩阵(经济欠发达,不缺水地区)

表9-29 工业节水指标两两比较判断矩阵(经济发达,缺水地区)

表9-30 工业节水指标两两比较判断矩阵(经济发达,不缺水地区)

表9-31 工业节水指标两两比较判断矩阵(经济欠发达,缺水地区)

表9-32 工业节水指标两两比较判断矩阵(经济欠发达,不缺水地区)

表9-33 第三产业节水指标两两比较判断矩阵(经济发达,缺水地区)
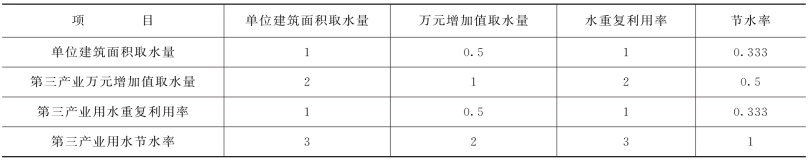
表9-34 第三产业节水指标两两比较判断矩阵(经济发达,不缺水地区)

表9-35 第三产业节水指标两两比较判断矩阵(经济欠发达,缺水地区)

表9-36 第三产业节水指标两两比较判断矩阵(经济欠发达,不缺水地区)

表9-37 居民生活用水节水指标两两比较判断矩阵(经济发达,缺水地区)

表9-38 居民生活用水节水指标两两比较判断矩阵(经济发达,不缺水地区)(https://www.xing528.com)

表9-39 居民生活用水节水指标两两比较判断矩阵(经济欠发达,缺水地区)

表9-40 居民生活用水节水指标两两比较判断矩阵(经济欠发达,不缺水地区)

表9-41 生态评价指标两两比较判断矩阵
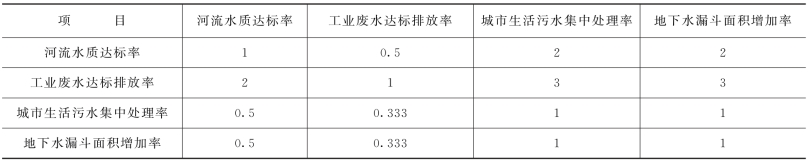
表9-42 节水管理指标两两比较判断矩阵

(2)评价指标相对权重的计算。计算各评价指标的相对权重,采用方根法进行层次单排序。
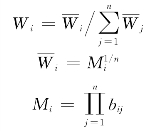
式中:Wi为各评价指标的权重;n为判断矩阵的阶数(指标个数);bij为两两指标间的标度值。
(3)进行一致性检验。计算结果需要进行一致性检验,首先计算特征根为

式中
(BW)i=∑bij·Wi
然后计算一致性比例为

式中:RI为平均随机一致性指标,见表9-43。
表9-43 2~10阶平均随机一致性指标

(4)确定权重。当CR<0.1时,则认为判断矩阵一致性可以接受,否则检查判断矩阵的合理性,修改判断矩阵后重新评价指标的相对权重,直到CR<0.1。这样就可以得出各级评价指标的权重W。
经过对计算结果的一致性检验和对判断矩阵的调整,计算得CR值见表9-44,权重见表9-45~表9-48。
表9-44 一致性检验结果(经济发达,缺水地区)

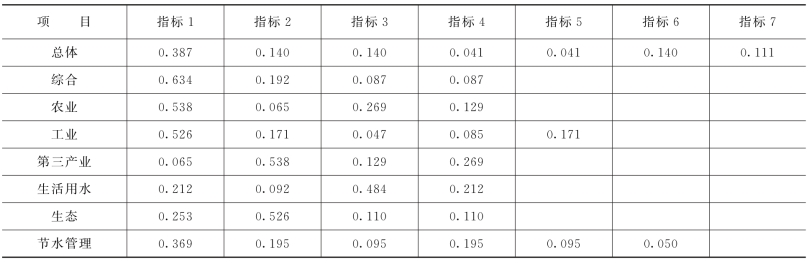
表9-45 指标权重(经济发达,缺水地区)

表9-46 指标权重(经济发达,不缺水地区)

表9-47 指标权重(经济欠发达,缺水地区)

表9-48 指标权重(经济欠发达,不缺水地区)
2.2.2 单层次评价模型的建立
(1)指标值的规范化处理。由于评价指标之间常具有不同的量纲和数量级,不能直接对比,因此要对原始指标进行规范化处理。首先,确定各指标的最大值Fm和最优值Fu,然后,对越大越优的指
标用式(9-1)变换,对越小越优的指标用式(9-2)变换。

经过式(9-1)或式(9-2)变换后的指标值在0~100之间,可以称其为标准值,标准值100最优,0最差。
(2)计算综合评价结果。
![]()

式中:R=[r1,r2,…,ri]为n个评价单位的综合评价结果矩阵;ri(i=1,2,…,n)为第i个单位的评价结果;W=[w1,w2,…,wk]为m个评价指标权重分配矩阵,wk(k=1,2,…,m)为第k个评价指标权重,应满足:![]() 为第i个单位第k种指标值。
为第i个单位第k种指标值。
计算结果是百分制值,可以认为90分以上为节水成绩优秀地区(城市);75~90分为节水成绩良好地区(城市);60~75分为节水成绩合格地区(城市);60分以下为不合格地区(城市)。
2.2.3 多层次综合评价模型
当系统方案各指标间分为不同层次时,需采用多层次综合评价模型。图9-2是以两个层次的综合评价模型为例给出的框图。
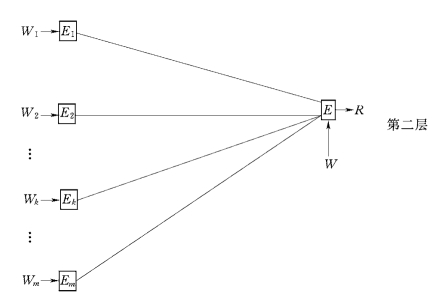
图9-2 两个层次综合评价模型框图
两层次综合评价是在单层次评价的基础上进行的,具体评价方法、步骤与单层次评价相同,如对K个指标进行单层次评价后,得到评价结果Rk(Rk=W·Ek),则进行第二层次的综合评价时,用Rk代替Ek,由公式(9-3)直接计算,便可得到各评价单位的评价结果。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




