博弈理论基本原理解析

3.1.1　博弈论的一般表达式

博弈论是研究决策主体的行为发生相互作用时如何决策以及这种决策的均衡问题的理论。博弈的要素包括：参与人（players）、行动（actions）、信息（information）、策略（strategies）、支付（payoffs）、结果（outcome）和均衡（equilibria）。参与人、行动和结果合起来称为博弈的规则（rules of the game），建立博弈模型的目的即在于运用博弈规则来确定均衡。

参与人是指做出决策的个体，每个参与人的目标都是通过选择行动来最大化自身的收益。行动或行为是参与人所能做的某一种选择，而行动集则是参与人可以选取的全部行动的集合。信息是参与人在特定时点对不同变量的了解。策略可以说是一项规则，即给定其信息集，该策略决定在博弈的每一时点该选择何种行动。支付是在所有的参与人都选择了各自的策略且博弈已经完成之后所获得的利益，也可表示参与人的期望效用，期望效用是关于所有参与人策略的函数。

均衡策略（equilibrium strategies）即纳什均衡。一个随机策略组合，当且仅当它对每一个参与人及该参与人的每一个策略而言，都满足其最大化期望支付条件，且不存在任何动机去改变自身的策略，则该策略组合称为均衡策略。均衡策略的个数可以是有限的，无限的，也可以是不存在的。

结果（outcome）即均衡支付，是指在博弈结束之后所获得的支付，或对应于各均衡策略的期望支付。

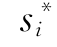若局中人的集合记作A，局中人的策略集合记作S，支付记作u，一个n人博弈可记为：G={A1，A2，…，Ai，…，An；S1，S2，…，Si，…，Sn；u1，u2，…，ui，…，un}。纳什均衡可定义为：战略组合是一个纳什均衡，如果对于每个i，是给定其他局中人选择的情况下第i个局中人的最优战略，即：。这时，任何一个局中人都无法通过单方面改变战略而获得更高的支付。(www.xing528.com)

根据局中人行动的先后顺序，非合作博弈可分为战略博弈与动态博弈两种形式。局中人同时决策的博弈称为战略博弈，局中人按照一定顺序决策的博弈称为动态博弈。动态博弈中，博弈被分为几个阶段进行，这种情况下，纳什均衡可扩展为子博弈精炼纳什均衡。

3.1.2　博弈论的应用领域

博弈论根据参与人是否能够达成有约束力的协议而分为非合作博弈和合作博弈。非合作博弈建立在给定约束条件下最大化自身效用函数的基础上，强调的是个人理性；而合作博弈是公理性的，常常诉诸于帕累托改进、效率和公平等，强调的是团体理性。但有时非合作博弈可以通过添加额外行动来实现合作博弈下的均衡。

1968年，格雷特·哈丁成功地将“囚徒的困境”与资源耗竭结合起来，揭示了生态环境问题产生的根本原因。而水资源作为一种有限而脆弱的资源，其管理的显著特征之一就是各管理主体之间行为的相互作用，因而博弈理论在水资源管理中得到了广泛的重视。它最初用于水资源联合工程的费用分配，由此发展了一系列公平的费用分配方法，如最小核心法、沙普利值法和纳什法。此后，它又被应用到水资源分配的研究当中，例如1995年Becker和Willian对太湖流域的全流域合作、美国和加拿大不合作、完全不合作三种情况的分配结果进行比较研究，得到不合作虽使某些州获得了局部利益但导致全流域整体利益受损的结论；而杨志峰等针对官厅水库跨边界区域水量水质问题进行了博弈分析，为优化该流域的水资源配置提供了支撑。

近年来，我国一些学者在这方面进行了很多有益的研究，其中，傅春、胡振鹏等人用合作博弈的理论与方法来解决综合利用水利工程中公共费用的分摊问题，周玉玺等用长期合作博弈理论研究了农村小流域灌溉组织制度，肖江文等建立了污水排放申报机制的不完全信息博弈模型，刘文强等利用博弈论对不同管理模式下流域水分配问题中用水冲突矛盾进行了分析和解释。这些研究显示了博弈论在水资源领域的应用价值和前景。