提梁机设计参数及结构强度验算

1）提梁机设计参数 900 t级提梁机、运梁车、架桥机是服务于现代化高速铁路建设中混凝土梁制造和安装的关键型设备。

900 t提梁机是用于生产车间和堆场之间预应力混凝土箱梁转运的专用设备。900 t提梁机的跨度为39 650 mm，起升净高度9 000 mm，额定负载900 t，可运送高速铁路客运专线32 m、24 m、20 m混凝土箱梁。提梁机的承载结构由双主梁构成，其底盘由拥有64只车轮的轮胎式底盘构成，这使得整车能在梁场自由运行。其具体的结构参数如下：

（1）提梁机自重：750 t。

（2）整车的总体尺寸：

①横向：0～5 100 mm高度范围内侧净宽度8 600 mm，5 100～9 000 mm高度范围内侧净宽度≥15 000 mm，总宽28 500 mm。

②纵向：内侧净距离35 000 mm，外侧尺寸44 300 mm。

（3）起升净高度：9 000 mm（混凝土梁顶面距地面）。

（4）卷扬机起升速度：满载为0.5 m／min，空载为1.5 m／min。

（5）整车行驶速度：满载为4 km／h，空载为6 km／h。

（6）整车行驶中的爬坡度：5%。

（7）重载的轮子接地比压≤0.6 MPa。

（8）最大风速：工作状态设计风速为6级；非工作状态设计风速为11级。

900 t提梁机采用了全液压传动，闭式液压走行系统和液压悬挂支撑方式，使众多轮胎组实现了均匀承载，并随道路的变化做自适应调整；液压全轮转向系统使超长的车体具有较小的转弯半径；液压卷筒起升系统使吊梁过程平稳。

2）提梁机行走系统驱动及功率计算

（1）行走阻力计算。假设地面的滚动摩擦阻力系数为0.025，最大爬坡度为5%。提梁机启动最大加速度为0.15 m／s2，回转质量为1.04，则可以通过如下公式计算行走阻力：

①重载平地阻力f重载平地计算公式为：

式中　m提——提梁机最大提升重量；

m梁——提梁机自重；

f摩——地面滚动摩擦阻力系数。

故计算得f重载平地＝41.25 t。

②空载平地阻力f空载平地计算公式为：

故计算得f空载平地＝18.75 t。

③重载坡度阻力f重载爬坡计算公式为：

式中　σ坡——最大爬坡度。

故计算得f重载爬坡＝82.5 t。

④空载坡度阻力f空载爬坡计算公式为：

故计算得f空载爬坡＝37.5 t。

⑤重载加速阻力f重载加速计算公式为：

式中　a——提梁机启动最大加速度；

m回转——回转质量。

故计算得f重载加速＝26 t。

⑥空载加速阻力f空载加速计算公式为：

故计算得f空载加速＝16 t。

（2）牵引力计算。

①空载平地牵引力F空载平地计算公式为：

故空载平地牵引力为F空载平地＝18.75 t。

②重载平地牵引力F重载平地计算公式为：

故重载平地牵引力为F重载平地＝41.25 t。

③空载坡度牵引力F空载爬坡计算公式为：

故空载坡度牵引力为F空载爬坡＝56.25 t。

④重载坡度牵引力F重载爬坡计算公式为：

故重载坡度牵引力为F重载爬坡＝123.75 t。

⑤空载平地加速牵引力F空载平地加速计算公式为：）

故空载平地加速牵引力为F空载平地加速＝34.75 t。

⑥重载平地加速牵引力F重载平地加速计算公式为：

故重载平地加速牵引力为F重载平地加速＝67.25 t。

（3）转向阻力计算。原地转向阻力矩计算公式为：

式中　G转——转向桥负荷，其最大值为总重量与转向桥之商，即）

f滚——轮胎滚动摩擦系数，其值为0.03；

f滑——轮胎滑动摩擦系数，其值为0.7；

l轮——轮胎接地面中心到转向中心线与地面交点间的距离，其值为1／2轮距，即为1.25／2＝0.625 m。

故可以计算得到T转＝100 693 N·m。

（4）发动机功率计算。计算时取传动系传动效率η为0.65，发动机储备系数τ为1.2。由于提梁机工作过程中功率消耗主要为行走工况、转向工况、重物起升工况，下面将分别介绍这几种工况下面发动机所需要的最大功率。

①行走工况。提梁机的行走分为重载平地行走和轻载平地行走，在这两种工况下单台发动机的功率消耗分别记为P重和P轻，计算公式分别为：

式中　v重和v空——整车重载和空载时的行驶速度；

n发动机——发动机转速。

故可以分别计算得到P重＝442 kW，P空＝288 kW。

②转向工况。在转向工况下，取转向速度v转＝0.8 r／min，则转向时单台发动机所需功率P转计算公式为：

故计算得到P转＝260 kW。

③预制梁提升工况。在预制提梁工况下，所需单台发动机功率P起升的值计算公式为：

故计算得P起升＝72 k W。

综上所述，发动机额定功率应大于等于442 kW（此功率应为除去空压机、进排气阻力等功率损失后的净功率）。

3）提梁机液压系统总体计算

（1）闭式行走液压系统元器件的确定。由前可知，对于闭式的行走系统，最终行走动力是由液压马达经过轮边减速器提供给行走驱动轮的。因此在确定闭式回路驱动马达的排量之前，先按照设计要求设计出轮边减速器的减速比。由行走阻力矩的计算公式可知，最大行走阻力矩计算公式为：

式中　F重坡——重载坡度牵引力；

r重——轮胎重载半径，r重＝715 mm。

故计算得T总＝884 812.5 N·m。

按照整车对称特性，在整车安装8个驱动桥，16个驱动马达，由此可以得到分配到单个驱动轮所需驱动力矩的大小计算公式为：

式中 n——驱动马达个数。

故计算得T马＝55 300 N·m。

由此选择轮边减速器型号为GFT0060T3，最大输出扭矩为60 000 N·m，传动比为139.9，带驻车制动，制动力矩为620 N·m。此时对应的马达型号为A6VE80。该轮边减速器输出转速26.8 r／min（马达排量最大时）或32.2 r／min（马达排量小于54时）。

根据实际工况要求，可以推算出提梁机轮胎的最大空载转速n空max和提梁机轮胎最大重载转速n重max，计算公式为：

式中　v空max和v重max——提梁机空载和重载时的最大车速，其中v空max＝6 km／h，v重max＝4 km／h；

r空和r重——提梁机空载和重载时的车轮半径，其中r空＝875 mm，r重＝715 mm。

故计算得n空max＝18.2 r／min＜32.2 r／min，n重max＝14.8 r／min＜26.8 r／min。

故所选轮边减速器和马达的型号满足使用要求。行走马达型号为A6VE80，带有速度传感器，采用比例电磁阀控制；其最大转速为3 750 r／min，最小转速为50 r／min，额定排量为80 m L，公称压力为40 MPa。行走系统所选泵为A4VG250闭式泵，额定排量为250 m L，公称压力为40 MPa，尖峰压力为45 MPa，最大转速为2 500 r／min，最小转速为500 r／min。

（2）转向液压系统元器件的确定。由于转向桥转可转角度为±100°，现假设转100°所需时间为20 s，即转速为0.8 r／min。转向油缸的行程为800 mm，由此可推算出油缸速度为1.2 m／min，由于转向油缸活塞直径为200 mm，活塞杆直径110 mm。发动机额定转速取1 800 r／min。故可计算出油缸所需流量为：

式中　s活塞——油缸横截面积。

故油缸所需流量计算为l＝40 L／min。

泵排量计算公式为：

故可得V泵排＝178 cm3。

则选取型号为A10VG190开式负载敏感泵，其额定排量为190 mL，公称压力40 MPa。

（3）起升液压系统元器件的确定。900 t提梁机起升系统同样采用液压马达带动卷扬机转动，同时卷扬机通过减速比为20的滑轮组绕起升钢丝绳吊重起升。其中，液压马达和卷扬机之间通过起升减速器进行过渡，在选定液压马达之前首先确定减速器的减速比，现由机械结构设计知道卷筒直径为1 200 mm，钢丝绳额定拉力14 t，则可知起升的额定力矩T起升为：

故可计算出T起升＝84 000 N·m。由此选择起升减速器型号为GFT110W3B215-04，其最大输出扭矩为100 000 N·m，满足起升扭矩要求，传动比为215，同时它还带驻车制动，制动力矩为750 N·m。

此时选择对应的马达型号为A6VE107，排量为107 m L，公称压力为40 MPa，最大转速为3 550 r／min，最小转速为50 r／min。由此可知该减速器输出转速为16 r／min（马达排量最大时）或26 r／min（马达排量小于68 m L时）。由于起升与转向工况是分别独立进行的，所以起升与转向等可以共用一个A10VG190开式负载敏感泵。液压系统中一个开式泵控制一个起升马达。现在需要验算在这种设计工况下最大重载起升速度v起升重载max、最大轻载起升速度v起升空载max、最大起升力矩T起升max以及额定和最大系统油压是否满足使用要求。

起升速度计算公式为：

故可计算得v起升空载max＝8 r／min＜26 r／min，v起升重载max＝2.67 r／min＜16 r／min。可以看出设计参数中所要求的最大轻载起升速度和最大重载起升速度均小于此液压系统所提供的最大速度，所以起升速度满足设计要求。

先根据公式验算最大起升力矩（计算时，以超过最大静载10%的过载量进行计算）

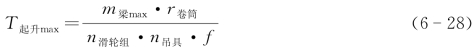
式中　n滑轮组——滑轮组个数；

n吊具——吊具数量。

故可计算得T起升max＝92 812.5 N·m＜100 000 N·m，因此起升力矩满足设计要求。

额定起升油压P额为额定起升力矩下的油压，最大起升油压pmax为最大起升力矩下的油压，计算公式如下：

故计算得P额＝23 MPa，pmax＝25.5 MPa。

由以上验算可知，所选取起升马达和起升减速器均符合设计要求。

4）提梁机制动系统受力分析 提梁机的制动方式分为驻车制动和行车制动。两种制动方式的受力形式不一样，现就分别对驻车制动和行车制动进行受力计算。

（1）驻车制动受力分析。驻车制动的受力分析主要为提梁机在一定坡度上制动时所能承受的最大制动力矩，并由此推算出重载和轻载情况下所能停放的最大驻车坡度。

驻车制动力矩公式为：

式中　T减——轮边减速器制动力矩；

i——减速比；

n——轮边减速器数量。

故可计算得T驻＝1 387 808 N·m。(www.xing528.com)

通过驻车制动力矩计算出空载最大驻车坡度σ空坡以及重载最大驻车坡度σ重坡，计算公式为：

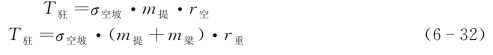
故可推算出空载最大驻车坡度为21%，重载最大驻车坡度为11%。超过这个坡度将会导致提梁机滑坡。

（2）行车制动受力分析。提梁机的行车制动分为静液压制动和气动制动。静液压制动是指泵的排量为0时，马达排量设为最大，地面附着力带动马达转动，马达产生阻力阻碍提梁机往前走，从而实现制动。此时整个行走液压系统受最大压力，即为系统溢流阀所调定的值。气动制动是指提梁机上有8个制动桥，每个制动桥上的两个轮子分别装有气动鼓式制动器来产生制动。鼓式制动器选择徐州金正公路工程机械有限公司的500 mm直径的制动器，可产生2 k N·m的制动阻力矩。

以下将分别计算静液压制动和气动制动情况下空载和重载的制动力、制动减加速度、制动距离等动态制动参数。

①静液压制动。

静液压制动情况下制动力矩T液阻计算公式为：）

式中　P系统——马达公称压力，P系统＝40 MPa；

V马达max——行走马达额定排量，V马达max＝80 m L；

n减速比——减速器减速比，n减速比＝139.9；

n马达——减速器输出转速，n马达＝16 r／min。

故可计算静液压制动情况下制动力矩T液阻＝1 140 007 N·m。

此情况下空载制动减加速度a空减计算公式为：

故可计算得a空减＝1.7 m／s2。

空载制动距离s空载计算公式为：

故可计算得s空载＝0.82 m。

同理可计算得到在重载情况下的制动减加速度a重减＝0.97 m／s2，制动距离s重载＝0.64 m。

②气动制动。

气动制动情况下制动阻力矩T气阻计算公式为：

式中　T毂——单个鼓式制动器所产生的制动力矩，T毂＝2 000 N·m；

n毂——鼓式制动器个数，n毂＝16。

故计算得T气阻＝32 000 N·m。

在此情况下空载制动减加速度a空减气计算公式为：

故可计算得a空减气＝0.5 m／s2。

则空载制动距离s空载气计算公式为：

故可计算得s空载气＝28.5 m。

同理可计算得到在重载情况下的制动减加速度a重减气＝0.027 m／s2，制动距离s重载气＝23 m。

5）提梁机结构强度验算

（1）提梁机钢结构建模。根据900 t提梁机的设计方案，进行总体验算之后，本节将利用有限元软件ANSYS对提梁机的金属结构进行强度验算，根据结构的特点，单元类型选用梁单元beam188。在建模中单位选用mm、s、kg。

提梁机的金属结构主要包括：双主梁、立柱、立柱间联系横梁等。根据设计图几何尺寸和截面尺寸，利用ANSYS建模分析。在建模中忽略了加强肋和焊缝等，因此将密度放大1.5倍，以下为建模计算的一些参数：

弹性模量：E＝2.06×1011 Pa；

泊松比：PRXY＝0.299；

密度：ρ＝7.85×1.5×1 000＝1.177 5×104 kg／m3；

ANSYS模型如图6-18所示，共1 095个节点，671个单元。

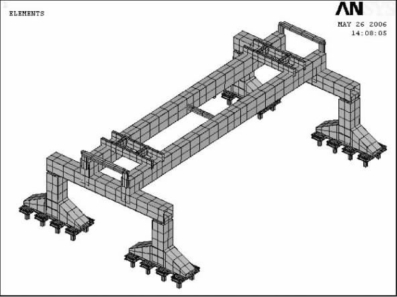
图6-18　900 t提梁机钢结构ANSYS模型

根据设计要求，提梁机可以运送四种不同规格的梁：32.6 m-900 t、24.6 m-686 t、20.6 m-545 t、16.5 m-450 t。在运送每一种规格的梁时，有四种工况，见表6-1。

表6-1　900t提梁机的运梁工况

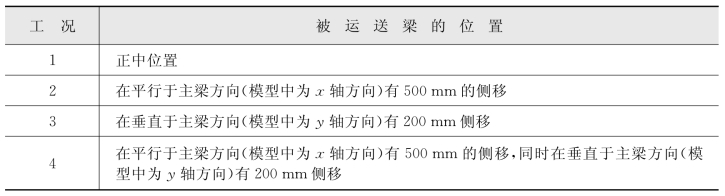
此外，假设在运送32.6 m-900 t规格的梁时，四个支腿不同步，其中三条支腿不动，第四条支腿每组轮子上沿平行于提梁机的运动方向（图6-18所示模型中x方向）施加6.25 t力。计算仅在自重作用下双主梁和端梁的变形。

按照上述运输工况及假设附加工况，建立的模型中采用如下两种约束：

①四种运输工况的约束情况：四条支腿均采用相同的约束，对每条支腿的一个轮子限制三个方向的移动自由度，其余几个轮子只限制竖直方向（图6-18所示模型中z方向）的移动自由度。

②假设附加工况的约束情况：三条支腿采用与上述工况相同的约束，第四条支腿限制每个轮子竖直方向上的移动自由度。同时限制一个轮子沿垂直于运动方向（图6-18所示模型中y方向）的移动自由度。

所受载荷主要为所吊吊具载荷和运输大梁载荷。其中，大梁载荷按其重量放大1.2倍后集中加载，吊具共四组，每组重量记为10 t，在其各自所在位置上进行集中加载。

（2）运送梁的规格为32.6 m-900 t。由表6-1中的说明可知，对于这种预制梁的运输下，钢结构需要分为四种工况进行验算。

①工况1，运输预制梁在正中位置，则应力加载模型如图6-19所示。全局应力如图6-20所示，由图可知最大应力为155.247 MPa，同样计算可知，最大应力集中在提升横梁上，双主梁的最大变形为75.087 mm，端梁的最大变形为26.183 mm。

图6-19　900 t大梁在正中位置时的应力加载图

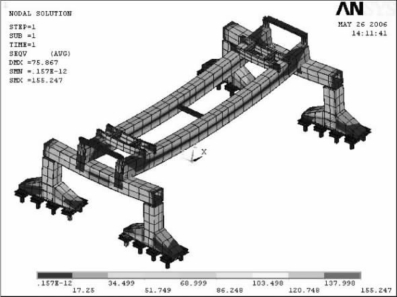
图6-20　900 t大梁在正中位置时的全局应力分布图（MPa）

②工况2，运输大梁在平行于主梁方向（模型中为x轴方向）有500 mm的侧移。全局应力如图6-21所示，这种工况下最大应力为157.536 MPa，最大应力出现在提升横梁上，双主梁的最大变形为75.101 mm，端梁变形最大为26.398 mm。

③工况3，运输大梁在垂直于主梁方向（模型中为y轴方向）有200 mm侧移。全局应力如图6-22所示，最大应力为159.784 MPa，由计算可知最大应力出现在提升横梁上，双主梁的最大变形为76.306 mm，端梁的最大变形为26.183 mm。

④工况4，被运送梁在平行于主梁方向（模型中为x轴方向）有500 mm的侧移，同时在垂直于主梁方向（模型中为y轴方向）有200 mm侧移。全局应力如图6-23所示，最大应力为162.067 MPa，由计算可知，最大应力出现在提升横梁上，双主梁的最大变形为76.322 mm，端梁的最大变形为26.398 mm。

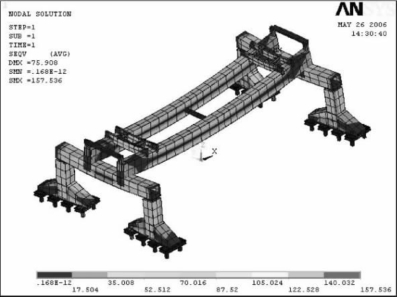
图6-21　900 t大梁在x方向侧移500 mm的全局应力分布图（MPa）

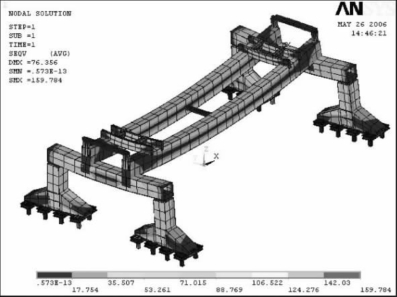
图6-22　900 t大梁在y方向侧移200 mm的全局应力分布图（MPa）

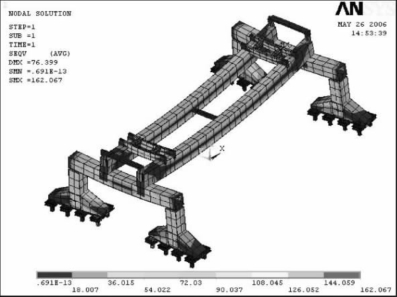
图6-23　900 t大梁同时在x、y方向上都有侧移的全局应力分布图（MPa）

（3）运送梁的规格为24.2 m-686 t。同样，900 t提梁机运输这种大梁的时候也需按照上面四种工况进行验算。

①工况1，运输大梁在正中位置，则应力加载模型如图6-24所示。这种工况下全局应力如图6-25所示，最大应力为128.009 MPa，最大应力出现在端梁上，双主梁的最大变形为89.259 mm，端梁的最大变形为23.362 mm。

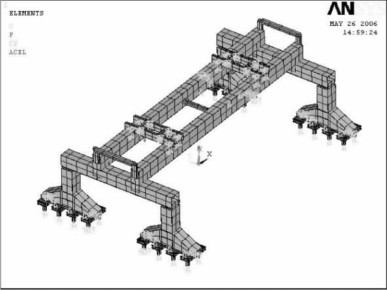
图6-24　686 t大梁在正中位置时的应力加载图

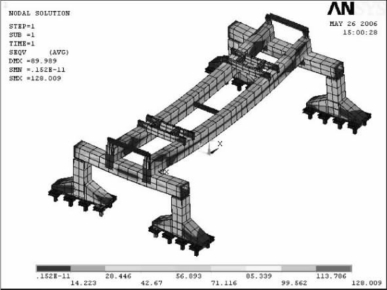
图6-25　686 t大梁在正中位置时的全局应力分布图（MPa）

②工况2，运输大梁在平行于主梁方向（模型中为x轴方向）有500 mm的侧移。全局应力如图6-26所示，最大应力为129.503 MPa，这种工况下最大应力出现在端梁上，双主梁的最大变形为89.252 mm，端梁的最大变形为23.667 mm。

③工况3，运输大梁在垂直于主梁方向（模型中为y轴方向）有200 mm侧移。全局应力如图6-27所示，最大应力为130.84 MPa，这种工况下最大应力出现在端梁上。双主梁的最大变形为90.984 mm，端梁的最大变形为23.362 mm。

④工况4，被运送梁在平行于主梁方向（模型中为x轴方向）有500 mm的侧移，同时在垂直于主梁方向（模型中为y轴方向）有200 mm侧移。全局应力如图6-28所示，最大应力为132.382 MPa，这种工况下最大应力出现在端梁上。双主梁的最大变形为90.976 mm，端梁的最大变形为23.667 mm。

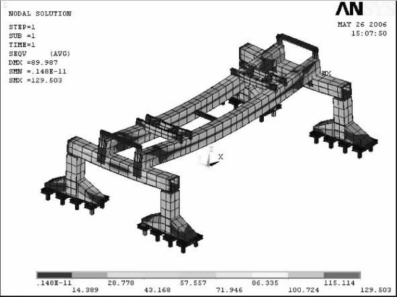
图6-26　686 t大梁在x方向侧移500 mm的全局应力分布图（MPa）

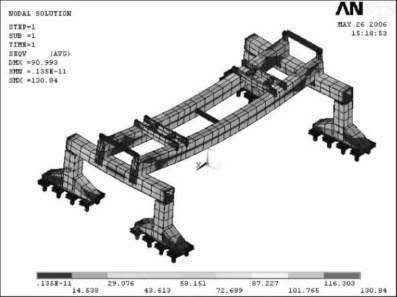
图6-27　686 t大梁在y方向侧移200 mm的全局应力分布图（MPa）

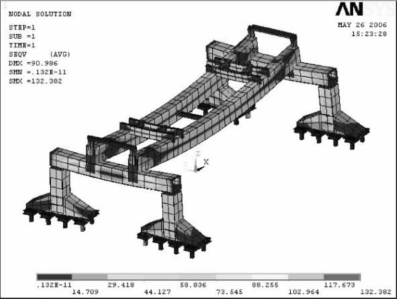
图6-28　686 t大梁同时在x、y方向上都有侧移的全局应力分布图（MPa）

（4）运送梁的规格为20.6 m-545 t。同样，900 t提梁机运输这种大梁的时候也需按照上面四种工况进行验算。

①工况1，运输大梁在正中位置，则应力加载模型如图6-29所示。全局应力如图6-30所示，最大应力为113.069 MPa，这种工况下最大应力出现在端梁上。双主梁的最大变形为84.889 mm，端梁的最大变形为20.397 mm。

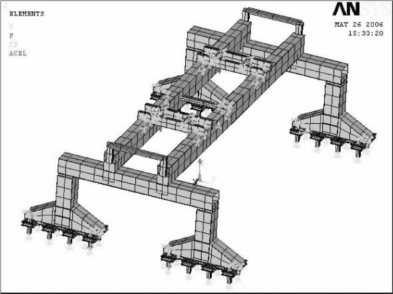
图6-29　545 t大梁在正中位置时的应力加载图（MPa）

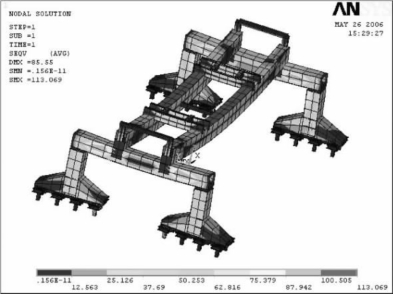
图6-30　545 t大梁在正中位置时的全局应力分布图（MPa）

②工况2，运输大梁在平行于主梁方向（模型中为x轴方向）有500 mm的侧移。全局应力如图6-31所示，最大应力为114.204 MPa，这种工况下最大应力出现在端梁上，双主梁的最大变形为84.883 mm，端梁的最大变形为20.674 mm。

③工况3，被运送梁在垂直于主梁方向（模型中为y轴方向）有200 mm侧移。全局应力如图6-32所示，最大应力为115.432 MPa，这种工况下最大应力出现在端梁上。双主梁的最大变形为86.588 mm，端梁的最大变形为20.397 mm。

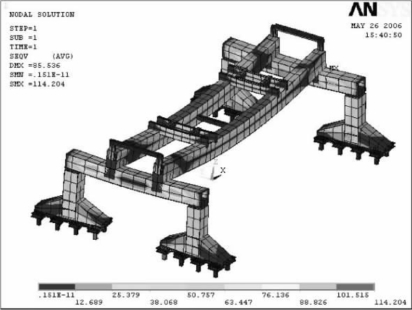
图6-31　545 t大梁在x方向侧移500 mm的全局应力分布图（MPa）

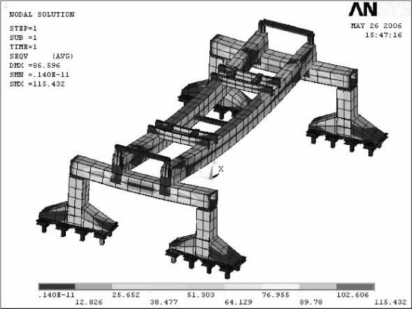
图6-32　545 t大梁在y方向侧移200 mm的全局应力分布图（MPa）

④工况4，被运送梁在平行于主梁方向（模型中为x轴方向）有500 mm的侧移，同时在垂直于主梁方向（模型中为y轴方向）有200 mm侧移。全局应力如图6-33所示，最大应力为116.611 MPa，这种工况下最大应力出现在端梁上。双主梁的最大变形为86.572 mm，端梁的最大变形为20.674 mm。

（5）运送梁的规格为16.5 m-450 t。同样，900 t提梁机运输这种大梁的时候也需按照上面四种工况进行验算。

①工况1，运输大梁在正中位置，则应力加载模型如图6-34所示。全局应力如图6-35所示，最大应力为111.789 MPa，在此工况下，最大应力出现在双主梁上，双主梁的最大变形为81.109 mm，端梁的最大变形为18.31 mm。

②工况2，被运送梁在平行于主梁方向（模型中为x轴方向）有500 mm的侧移。全局应力如图6-36所示，最大应力为112.936 MPa，在此工况下应力最大出现在双主梁上。双主梁的最大变形为81.088 mm，端梁的最大变形为18.561 mm。

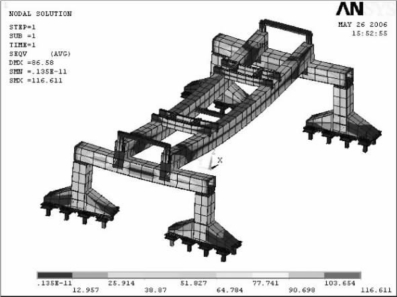
图6-33　545 t大梁同时在x、y方向上都有侧移的全局应力分布图（MPa）

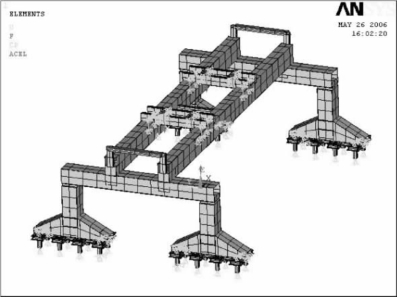
图6-34　450 t大梁在正中位置时的应力加载图

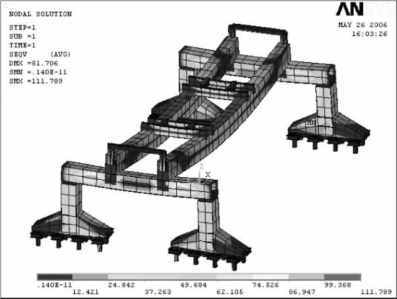
图6-35　450 t大梁在正中位置时的全局应力分布图（MPa）

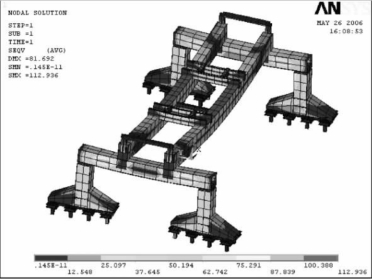
图6-36　450 t大梁在x方向侧移500 mm的全局应力分布图（MPa）

③工况3，被运送梁在垂直于主梁方向（模型中为y轴方向）有200 mm侧移。全局应力如图6-37所示，最大应力为114.892 MPa，在此工况下，最大应力出现在双主梁上。双主梁的最大变形为82.758 mm，端梁的最大变形为18.31 mm。

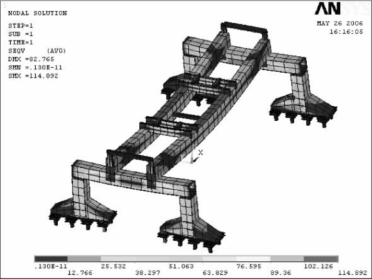
图6-37　450 t大梁在y方向侧移200 mm的全局应力分布图（MPa）

④工况4，被运送梁在平行于主梁方向（模型中为x轴方向）有500 mm的侧移，同时在垂直于主梁方向（模型中为y轴方向）有200 mm侧移。全局应力如图6-38所示，最大应力为116.202 MPa，这种工况下最大应力出现在双主梁上，双主梁的最大变形为82.736 mm，端梁的最大变形为18.561 mm。

（6）附加工况。由建模时的假设可知，在计算四种规格大梁运输的受力分析之后，还进行了一个假设附加工况的约束计算。在运送32.6 m-900 t规格的大梁时，假设运送大梁在正中位置。三条支腿不动，第四条支腿每个轮子上沿平行于提梁机的运动方向（模型中x方向）施加6.25 t力。

在此工况下加载后的模型如图6-39所示。全局应力如图6-40所示，最大应力为155.199 MPa，最大应力在提升横梁上，主梁的最大变形为77.058 mm，端梁的最大变形为26.885 mm。

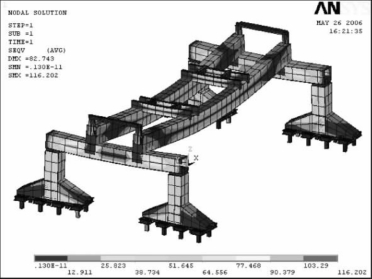
图6-38　450 t大梁同时在x、y方向上都有侧移的全局应力分布图（MPa）

图6-39　附加工况下应力加载图

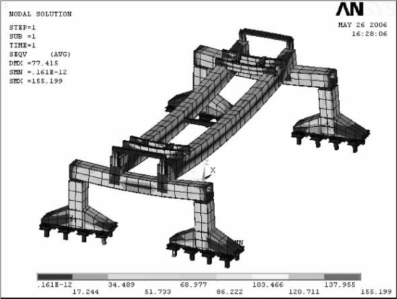
图6-40　附加工况下应力分布图（MPa）

（7）车架的应力分析及自重作用下双主梁和端梁的变形分析。

①车架的应力分析。当运送32.6 m-900 t规格的大梁时，被运送梁在平行于主梁方向（模型中为x轴方向）有500 mm的侧移，同时在垂直于主梁方向（模型中为y轴方向）有200 mm侧移，此时车架处于最不利工况。这时车架的应力图如图6-41所示，最大应力为108.6 MPa。

图6-41　车架的应力图（MPa）

②自重作用下双主梁和端梁的变形。自重作用下双主梁的变形如图6-42所示，最大变形为17.353 mm。自重作用下端梁的变形如图6-43所示，最大变形为5.439 mm。

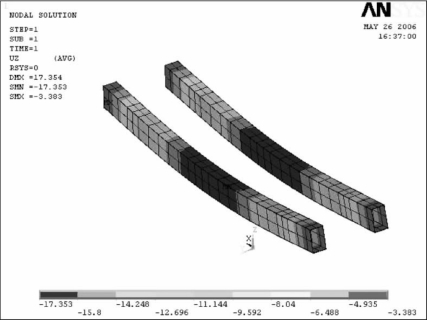
图6-42　自重作用下的双主梁变形图（mm）

（8）结果比较及结论。综上所述，计算了运送不同规格梁，不同工况下的应力、变形情况，现将结果列于表6-2中。

图6-43　自重作用下端梁变形图（mm）

表6-2　4种梁在各种工况下的应力、变形表

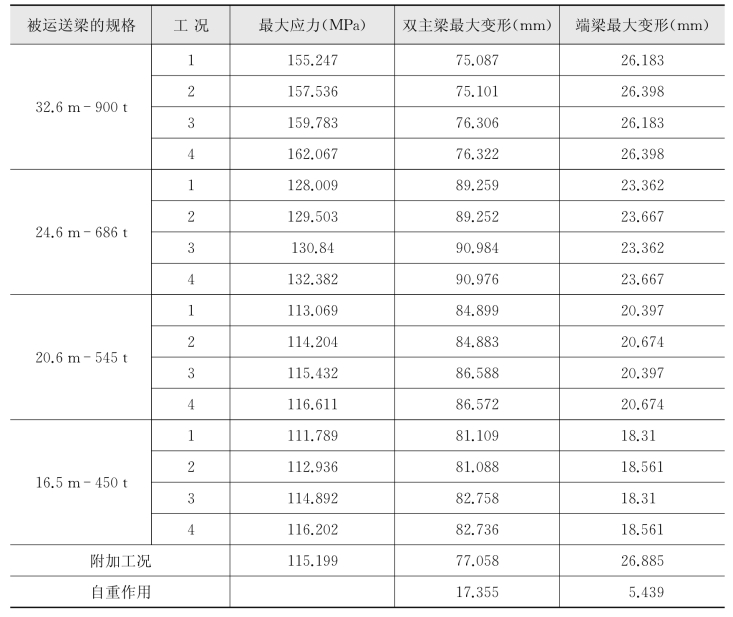
由表6-2可知，最大应力出现在端梁上，为162.067 MPa，小于许用应力。特别指出，在运送不同规格梁时，端梁应力的变化范围是102.287～151.838 MPa，双主梁的应力变化范围是79.859～116.202 MPa。

主梁的最大变形为90.984 mm，端梁的最大变形为26.885 mm，变形量也在允许的范围以内。仅在自重作用下，主梁的最大变形为17.355 mm，端梁的最大变形为5.439 mm。