在顶推过程中,梁体内力不断地发生变化,梁段各截面在经过支点时承受负弯矩,在经过跨中区段时产生正弯矩,全桥每个截面的内力都要不断地变化:负弯矩—正弯矩—负弯矩。另一方面,钢箱梁在顶推施工中经过桥墩时,它的底板会受到滑道的反力作用。由于整个钢箱梁底部的横向加劲肋疏密程度不同,顺桥向不同部位的箱梁底部所能承受的滑道反力大小也就不同。以九堡大桥主梁步履式顶推为例进行有限元分析。取两个最不利的工况予以分析,其一为最大悬臂状态,支座处反力大弯矩大;其二为主梁上墩(导梁处悬臂状态),此时主梁近0.4L处有弯矩最大值。
1)有限元模型说明
(1)选用单元说明。主梁部分(包括顶底板、腹板、加劲肋)选用板壳单元shell93,不同的板厚通过赋不同的实参得到。
经第二节分析,仅确定导梁较为粗略的几个参数,故导梁部分选用beam44单元,其主要参数如下:
导梁与主梁的跨径比为:![]() 。
。
导梁与主梁的单位长自重比为:![]() 。
。
导梁与主梁的刚度比为: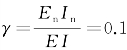 。
。
横向支撑系统用beam44单元,其截面如图4-70所示。斜撑截面如图4-71所示。
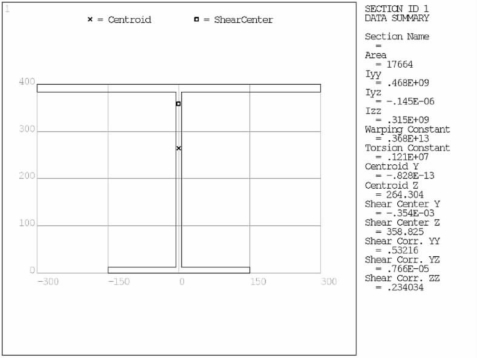
图4-70 横撑截面示意图
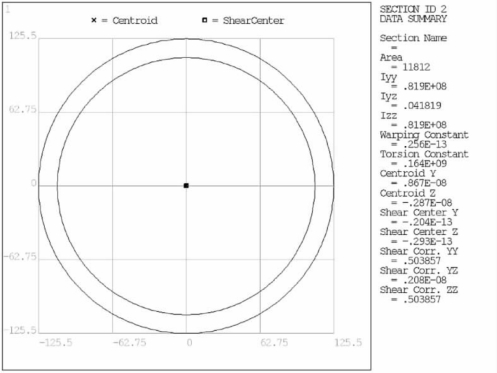
图4-71 斜撑截面示意图
(2)连接说明。由于主梁和导梁选用了不同类型的单元,故而涉及shell93和beam44单元之间连接的问题,利用ANSYS中cerig命令在连接处做刚域耦合处理,即保证其线位移、角位移一致。连接部分如图4-72所示。
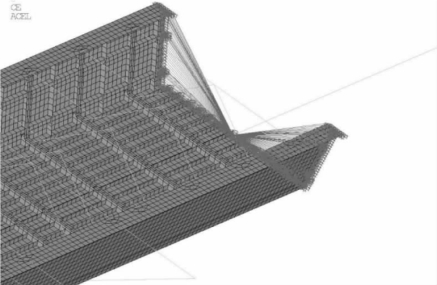
图4-72 刚域区域示意图
(3)荷载和支承条件。荷载仅考虑槽形钢箱梁本身的自重。每侧滑槽顶部聚四氟乙烯板与主梁的接触面积为1 600 mm×250 mm,采用固定该区域内节点的线位移。
2)最大悬臂状态
(1)全桥模型如图4-73所示。取出一节段局部放大,并显示杆系单元(横向支承系统)的截面如图4-74所示。
(2)应力计算结果。
①变形图如图4-75所示。

图4-73 最大悬臂状态时全桥模型
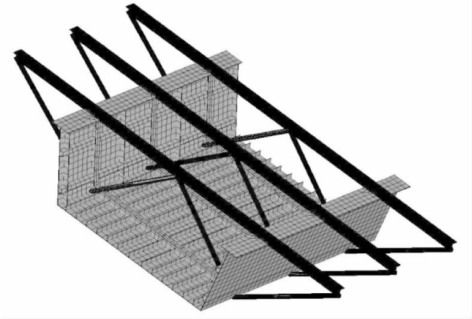
图4-74 横向支承系统示意图

图4-75 变形图(mm)
②支座处x向应力如图4-76所示。
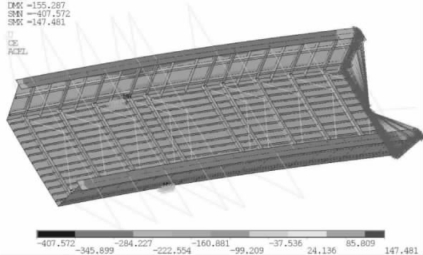
图4-76 支座处x向应力图(MPa)
③von mises应力云图如图4-77所示。

图4-77 von mises应力云图(MPa)
(3)稳定计算结果如图4-78所示。
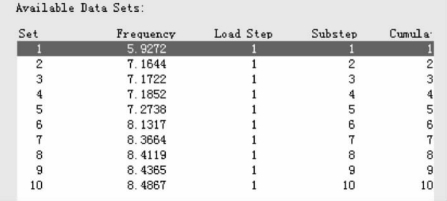
图4-78 稳定计算结果(Hz)
①一阶失稳模态(滑道附近底板失稳)如图4-79所示。(https://www.xing528.com)
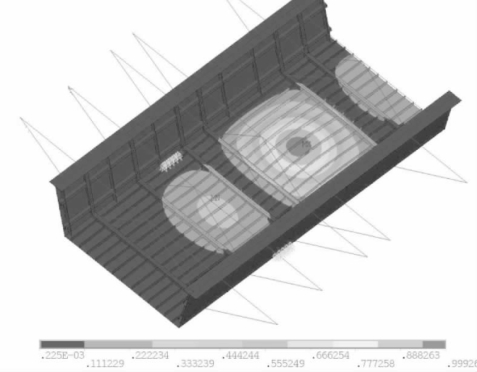
图4-79 一阶失稳模态(mm)
②二阶失稳模态(滑道附近腹板及其加劲肋屈曲)如图4-80所示。
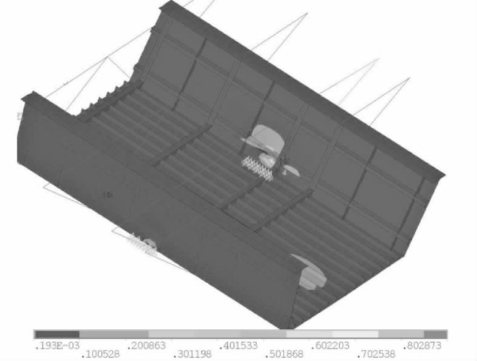
图4-80 二阶失稳模态(mm)
③三阶时仍为腹板处失稳。
④四阶失稳模态(滑道附近纵向加劲肋屈曲)如图4-81所示。
3)主梁上墩
(1)应力计算结果。
x向应力分布如图4-82所示。
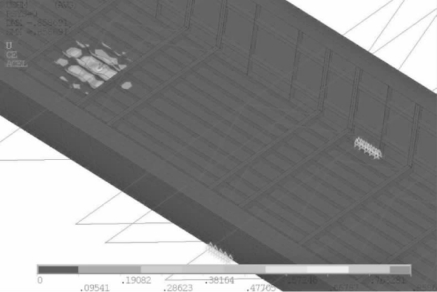
图4-81 四阶失稳模态(mm)
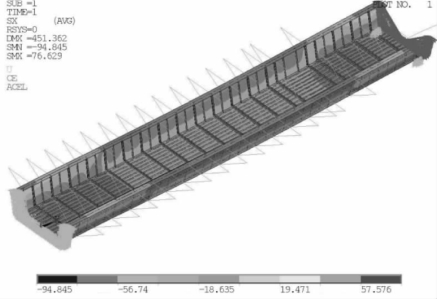
图4-82 x向应力分布(MPa)
von mises应力云图如图4-83所示,取支座附近的单元放大,如图4-83所示。
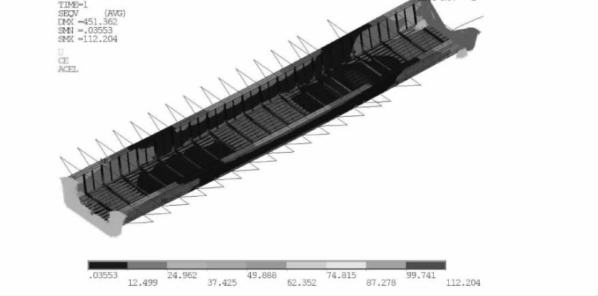
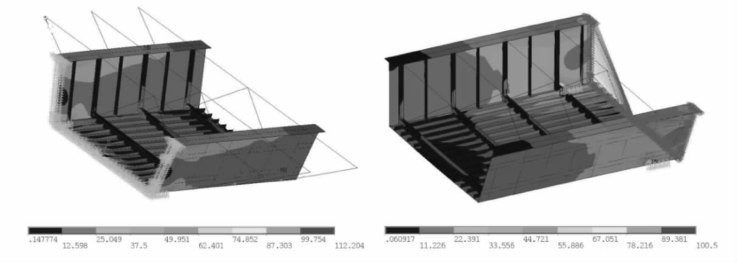
图4-83 应力云图(MPa)
(2)稳定计算结果如图4-84所示。
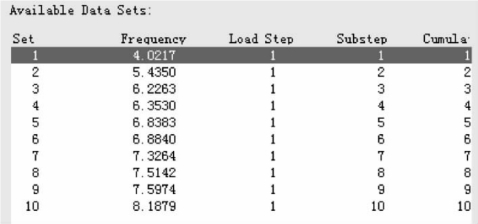
图4-84 稳定计算结果(Hz)
①一阶失稳模态(滑道附近腹板屈曲)如图4-85所示。
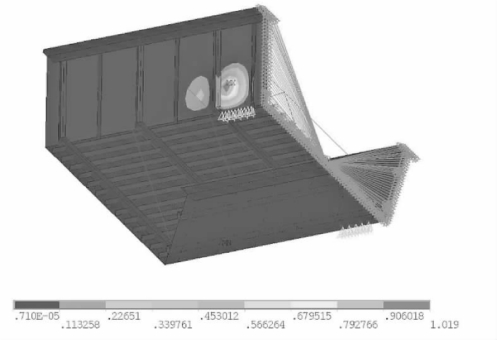
图4-85 一阶失稳模态(mm)
②二阶失稳模态(Mmax处腹板及其加劲肋屈曲)如图4-86所示。

图4-86 二阶失稳模态(mm)
③三阶失稳模态(Mmax处腹板及其加劲肋屈曲)如图4-87所示。
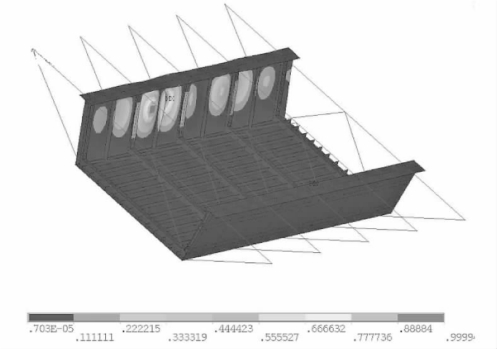
图4-87 三阶失稳模态(mm)
④四阶失稳模态(滑道附近腹板屈曲)如图4-88所示。
经有限元分析,顶推过程中强度满足要求。
根据有限元计算结果,施工过程中若是仅考虑自重,不会出现整体失稳的情况。模型的十阶模态均表现为局部失稳,局部失稳中既有腹板的局部失稳,也有底板的局部失稳。在顶推过程中,支座附近的腹板和底板在较大的支反力和负弯矩作用下可能会出现局部屈曲;弯矩最大处的腹板及其加劲肋可能会出现局部屈曲。
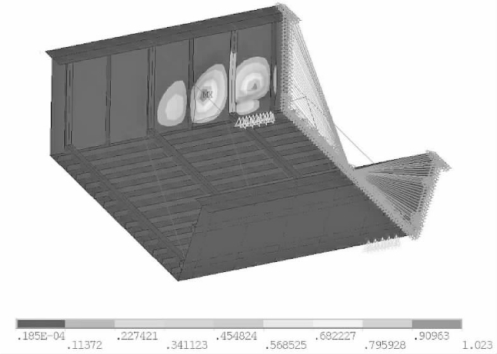
图4-88 四阶失稳模态(mm)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




