桥梁结构现代施工技术：稳定分析与顶推施工

以九堡大桥施工为例，对主梁进行整体稳定性分析。

1）作用在主梁上的荷载 最大悬臂时，悬臂端M＝－124 236.1 k N·m。作用在支架杆件上的风荷载按照《公路桥涵设计通用规范》（JTGD60—2004）计算。

横桥向风荷载标准值可以按照下式计算：

式中　Fwh——横桥向风荷载标准值（k N）；

Wd——基本风压（k N／m2）；

W0——设计基准风压（k N／m2）；

Awh——横向迎风面积（m2），按桥跨结构各部分的实际尺寸计算；

V10——桥梁所在地区的设计基本风速（m／s），系按平坦空旷地面，离地面10 m高，重现期为100年10 min平均最大风速计算确定；当桥梁所在地区缺乏风速观测资料时，V10可按“全国基本风速图及全国各气象台站基本风速和基本风压值”的有关数据并经实地调查核实后采用；

Vd——高度Z处的设计基准风速（m／s）；

Z——距地面或水面的高度（m）；

γ——空气重力密度（k N／m3）；

k0——设计风速重现期换算系数，对于单孔跨径指标为特大桥和大桥的桥梁，k0＝1.0，对其他桥梁，k0＝0.90；对施工架设期桥梁，k0＝0.75；当桥梁位于台风多发地区时，可根据实际情况适度提高k0值；

k3——地形、地理条件系数；

k5——阵风风速系数，对A、B类地表k5＝1.38，对C、D类地表k5＝1.70；

k2——考虑地面粗糙度类别和梯度风的风速高度变化修正系数；

k1——风载阻力系数；

g——重力加速度，g＝9.81 m／s2。

百年一遇的标准设计风速为28.6 m／s。

表4-5　主梁的风荷载

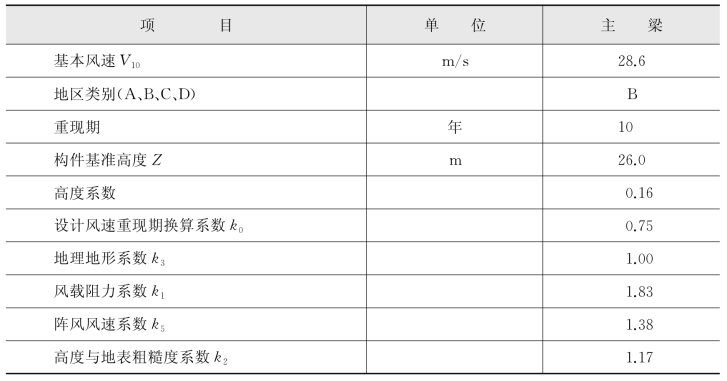
（续表）

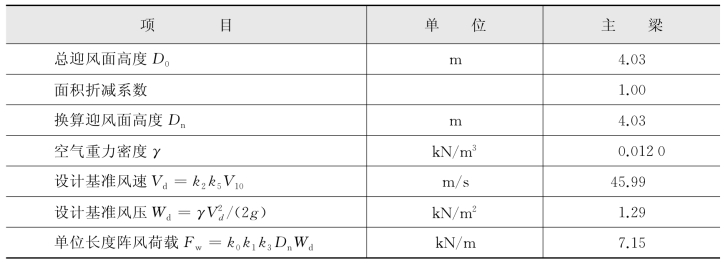
最大悬臂时，悬臂端M＝25 829.4 k N·m。

2）弯扭稳定计算方法 受弯的等截面实腹式构件的整体稳定应满足下列公式：

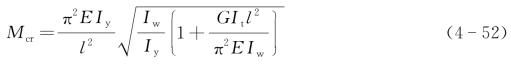
式中　Mx，My——所计算构件段范围内的最大弯矩；

Wx，eff，Wy，eff——考虑剪力滞和受压板件局部稳定的有效截面模量；

βm——等效弯矩系数；

φbx——弯矩作用平面内的受弯构件稳定系数；

Mcr——整体失稳的临界弯矩（弯扭屈曲临界弯矩）。

（1）整体失稳的临界弯矩的计算说明。当构件的支承条件、荷载作用方式、截面形状等发生改变，则整体失稳的临界弯矩需作修正：

①支承条件变化时。

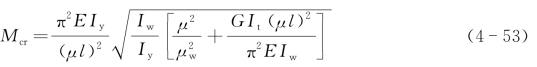
悬臂状态时，μ＝2，μw＝2。

②荷载作用方式变化时。荷载作用方式改变引起构件上弯矩分布形状的改变。由受弯构件弯扭失稳的机理可知，弯矩分布图形越饱满，受压翼缘的应力分布越均匀，相邻截面之间相互支持作用就越小，所以做β1倍的修正。

β1为荷载作用方式系数，纯弯曲时取1.0；满跨均布荷载时取1.3；跨中中央一点集中荷载时取1.35；两端作用等值反向弯矩时取2.65。

③截面形式变化时。当两端简支构件为单轴对称截面，且失稳前外力作用使构件绕非对称轴挠曲时，其临界弯矩表达式为：

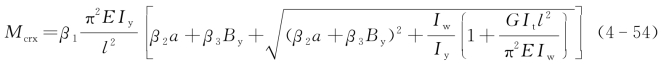
式中　a——横向荷载作用点至剪力中心的距离，当荷载作用点到剪力中心的指向与挠曲方向一致时取负，否则取正；(www.xing528.com)

By——参数，反映截面不对称的程度。

计算公式为

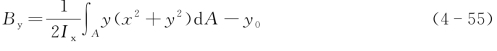
式中　y0——剪力中心S至形心的距离，当剪力中心到形心的指向与挠曲方向一致时取负，否则取正；

β2、β3——与荷载类型有关的系数，纯弯曲时分别为0、1；满跨均布荷载时，分别取0.46、0.53；跨中中央一点集中荷载时，分别取0.55、0.40。

（2）弯矩作用平面内的受弯构件稳定系数的计算说明。按式（4-51）计算所得的柔度系数按轴心受压整体稳定系数的计算公式计算受弯构件稳定系数，公式如下：

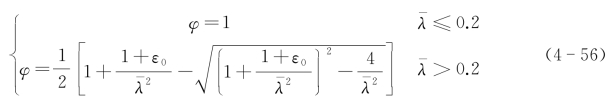
式中，ε0＝α（λ－－0.2）。

3）稳定校核 简化计算的假定：认为最大悬臂状态时，悬臂部分各个截面的几何特性保持不变，即不考虑梁段间尺寸的不同，不考虑导梁的不同。最大悬臂状态时，M图形状可知Kc＝0.91。

（1）截面几何特性。

惯性矩为Ix＝2.845 187 048×1012 mm4；Iy＝2.525 400 677×1013 mm4。

扇形惯性矩为Iw＝4.961 735 092×1019 mm4。

抗扭惯矩为It＝1.461 558 459×109 mm4。

（2）其他参数：

β1＝1.3；

β2＝0.46；

β3＝0.53；

a＝－3 346 mm（横向荷载仅自重，所以认为作用在截面的形心处，取形心到剪力中心的距离）；

y0＝3 346 mm；

l＝85 000 mm；

μ＝2，μw＝2；

简化计算，不考虑腹板及加劲肋时

∫A y（x 2＋y 2）d A＝2 627×（2.617 9×1011＋1.627 0×1012）

－1 405×（3.573 4×1011＋1.803 9×1012）

＝1 925 449 630 000 000

则代入式（4-55）可计算得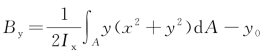＝－3 007.6。

将上述数据代入式（4-54），可计算得Mcrx＝71 227.8 k N·m；通过式（4-48）可计算得Mux＝526 511.48 k N·m；通过式（4-49）可计算得Muy＝1 187 349.32 k N·m；通过式（4-50）可计算得，取值为1.0；通过式（4-51）可计算得；通过式（4-56）且由于，可计算得φ＝0.08。

通过式（4-46）和式（4-47）来验证是否满足要求。经计算

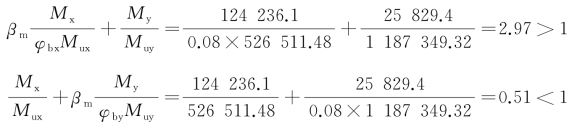
不满足式（4-46）要求。

4）解决方案 为九堡桥设计一纵平联，截面为T形，如图4-67所示。经计算其截面积S＝10 800 mm2。采用的布置形式如图4-68所示。图中h＝13 000 mm；a＝4 250 mm；d＝13 677.1 mm。

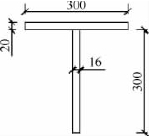
图4-67　T形截面

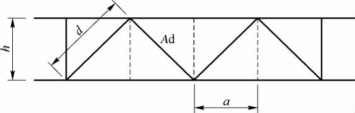
图4-68　布置形式

采用抗剪刚度相等的原则来确定连续化后薄壁箱梁的板壁厚度。一个平面桁架的一个节间承受一个单位剪力V＝1的情形，剪切变形公式为：

桁架的剪切刚度计算公式为：

因此根据式（4-57）和式（4-58）可以得到：

由抗剪刚度相等的原则，可得到连续化后的拟腹板厚度为：

因此，可以计算得到t＝0.608 mm。

从而得到一个闭合的箱型断面，利用ANSYS计算该截面的几何特性，如图4-69所示。

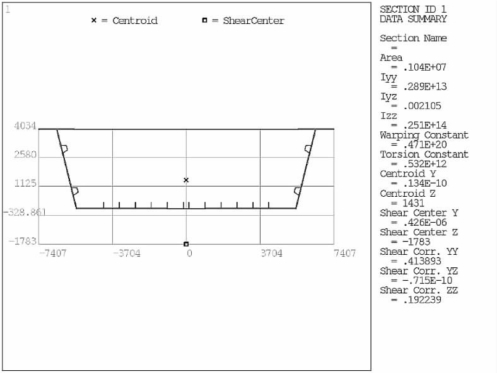
图4-69　截面几何特性

调出数据：惯性矩Ix＝2.886 542 487×1012 mm4，Iy＝2.507 747 206×1013 mm4；扇形惯性矩Iw＝4.705 939 461×1019 mm4；抗扭惯矩It＝5.316 881 326×1011 mm4；a＝－3 214 mm，y0＝3 214 mm；Mcrx＝9 932 875.862 k N·m；Mux＝524 460 k N·m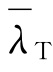；＝0.26；βm＝0.98；ε0＝0.048，φ＝0.95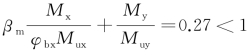；，满足要求。