主梁内力分析：顶推施工导梁实施现况

（1）为反映理想的顶推过程中导梁各参数对主梁受力的影响以确定主梁受力最不利工况，分析中对导梁主梁解析模型做如下假设：

①导-主梁如同一个整体，完整地结合在一起。

②导梁与主梁分别具有均一的重量和刚度。

③忽略支座沉降及误差等引起的其他次内力的影响。

为了便于绘图和分析比较，以下各弯矩和支点反力的数值均采用无量纲的形式表示。

设导梁的长度为ln，主桥每跨的跨度为l，导梁长度与每跨跨度的比值用无量纲的参数α表示，α＝ln／l；导梁的单位长度的自重为qn，槽形钢主梁的单位长度的自重为q，导梁单位长度的自重与钢主梁单位长度的自重的比值用无量纲的参数β表示，β＝qn／q；导梁刚度为En In，钢主梁刚度为E I，导梁刚度与钢主梁刚度的比值用无量纲的参数λ表示，λ＝En In／EI。这样，对于确定桥梁在顶推施工中最优的导梁参数的问题，就是如何确定上面所给出3个参数的最优组合的问题。

以主梁的前端刚好在B墩墩顶位置时的工况为起点，此时主梁前端的导梁有最大的悬臂长度ln。随着顶推施工的进程不断推进，主梁位置不断变化，设主梁前端与B墩的距离为x，用无量纲的参数λ＝x／l来表示梁体的位置，则此时B墩墩顶位置的弯矩可以表示为λ以及导梁、主梁的参数α、β、γ的函数，按照导梁前端是否到达前方桥墩，可以将顶推过程分为两个阶段。

第一阶段：0≤λ＜1－α，计算简图如图4-51所示。

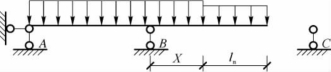
图4-51　顶推第一阶段计算简图

第二阶段：1－α≤λ＜1，计算简图如图4-52所示。

图4-52　顶推第二阶段计算简图

（2）最大负弯矩分析。(www.xing528.com)

①为分析导梁刚度在顶推施工阶段对主梁内力的影响，假设α＝0.55，β＝0.2，利用ANSYS建模分析，就可得到不同γ值下在整个跨度的顶推过程中B支点的弯矩值MB，如图4-53所示。

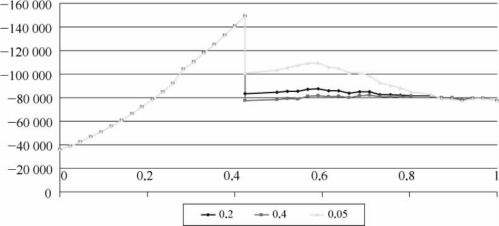
图4-53　不同γ值对最大负弯矩的影响

从图中可以看出，在A—B跨顶推过程的开始阶段，主梁与钢导梁的前端为悬臂，MB的值随着顶推长度的增大而不断增大；当导梁前端到达前面的A墩顶的位置的时候，即λ＝（1－α）时，导梁受到A支点反力的作用，使B墩处的弯矩突然减小，在此阶段内，刚度变化的影响不大。当导梁上墩后，导梁的刚度对顶推主梁MB值有很大影响，当相对刚度比γ值较小时，导梁越过前方支点到达某一特定位置时，主梁出现很大的负弯矩峰值，随着γ值的增大，导梁越过前方支点的负弯矩MB峰值减小。

②为分析导梁长度在顶推施工阶段对主梁内力的影响，假设β＝0.1，γ＝0.2，利用ANSYS分析得到在不同α值下在整个跨度的顶推过程中B支点的弯矩值MB，如图4-54所示。

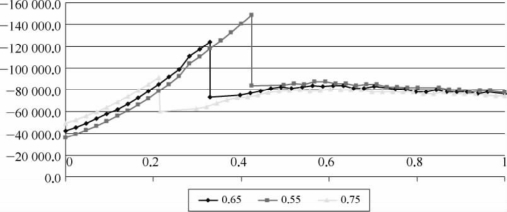
图4-54　不同α值对最大负弯矩的影响

从图中可以看出，导梁的相对长度对顶推主梁在悬臂根部的负弯矩MB的峰值有很大影响。若导梁较短（如α＝0.55），将使悬臂根部产生很大的负弯矩峰值，而若导梁较长，悬臂根部的负弯矩值很小；当导梁越过前方支点以后，导梁的长度对主梁B墩处的负弯峰值的影响较小。

③为分析导梁相对重度在顶推施工阶段对主梁内力的影响，假设α＝0.65，γ＝0.2，利用ANSYS得到在不同β值下在整个跨度的顶推过程中B支点的弯矩值MB，如图4-55所示。

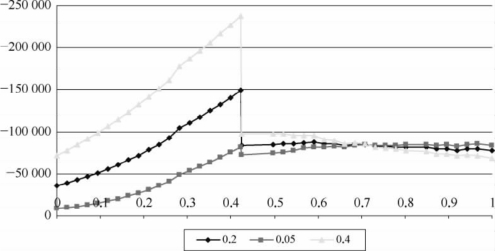
图4-55　不同β值对最大负弯矩的影响

从图中可以看出，导梁的相对重度对主梁在最大悬臂状态时的负弯矩峰值同样有很大影响。导梁较重时，悬臂根部的负弯矩峰值较大，导梁较轻时，主梁悬臂根部的负弯矩峰值则较小；当导梁越过前方支点以后，导梁相对重度对B支点处的负弯矩值的影响没有主梁悬臂时那么明显。

（3）最大正弯矩分析。导梁的各参数值并不决定主梁第一跨内的最大正弯矩值，主梁的最大正弯矩值主要由主梁的本身尺寸决定。由此就可以认为在导梁的优化分析中，第一跨跨内的最大正弯矩对导梁参数的设计不起决定作用，导梁参数根据顶推过程B支座位置的最大负弯矩来确定。