
图4-19 力学示意图
如图4-19所示,多点分散顶推的能够实现的条件是:
![]()
式中 Fi——第i个支座处的顶推动力装置的顶推力;
Ni——第i个支座处的支点瞬时(最大)支反力;
fi——第i个支座处的支点装置的相应摩擦系数;
ai——支座纵坡率,“+”为上坡顶推,“-”为下坡顶推。
多点顶推与集中单点顶推相比较,可以避免配置大型顶推装备,能有效地控制顶推时梁体的偏移,顶推时对支座的水平推力可减小到很小。但多点顶推需要较多的设备装置,操作时的同步性等要求甚高。
选择连续顶推装备的主要依据为:满足顶推力的计算要求;顶推力与摩擦力的合力必须小于支座许用的最大水平力。
此时,多点分散连续顶推施工的动力学基础数学描述表达式可改写为:

式中 F′i——第i支座油缸施加力;
f′i——第i支座水平摩擦力。
连续顶推的主要的目的是把顶推装备分散于各个支座上,分散各支座水平反力。如果油缸施力之和小于梁体承受的所有支座水平摩阻力之和,则梁体不会移动。如上所述的多点顶推力学模型只适用于桥体在持续顶推的过程,而在顶推启动和停止的阶段未做详细的探讨。为了给指导施工实践提供理论依据,在上述基础上研究顶推启动和停止阶段的力学模型。以下以顶推启动阶段为例进行力学分析。
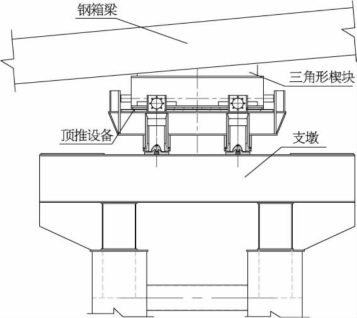
图4-20 多点顶推力学模型
在顶推施工时,顶推装备的顶升油缸支撑于桥墩或临时支墩之上。同时在顶推装备参与顶推时,钢箱梁与顶推装备接触面处存在一定的角度,此时需要在顶推装备与钢箱梁之间放置三角形楔块来保证结构的平稳性,如图4-20所示。
施工过程中,顶升支撑油缸将桥梁梁体、上部滑移结构和下部支承结构托起,利用顶推移动油缸在上部滑移结构和下部支承结构之间施加水平推力P,使得顶推装备在上部滑移结构和下部支承结构之间产生相对滑动,上部滑移结构带动桥梁梁体前移。
现分别对钢箱梁、三角形楔块、顶推装备上部滑移结构、下部支撑结构进行受力分析。假设钢箱梁与顶推装备处的夹角为α,重力加速度为g。钢箱梁质量为M0,重量为G0,所受到的支反力为N0,摩阻力为Fs0,加速度为a0;三角形楔块的质量为M1,重量为G1,所受到的支反力为N1,摩阻力为Fs1,加速度为a1;上部滑移结构的质量为M2,重量为G2,所受到的支反力为N2,摩阻力为Fs2,加速度为a2;下部支撑结构的质量为M3,重量为G3,所受到的支反力为N3,摩阻力为Fs3,加速度为a3。钢箱梁与三角形楔块之间、三角形楔块与上部滑移结构之间、上部滑移结构与下部支撑结构之间、下部支撑结构与支墩之间的摩擦力系数分别为μ0、μ1、μ2、μ3。
首先以钢箱梁为对象,如图4-21所示。由平衡条件有:
![]()
![]()
![]()
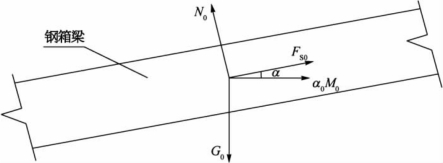
图4-21 钢箱梁顶推过程的力学模型
以三角楔块为研究对象,如图4-22所示。由平衡条件有:
![]()
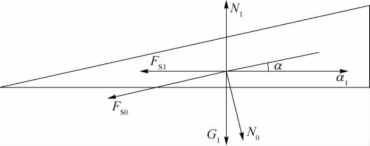
图4-22 三角形楔块顶推过程的力学模型
则可得:

以顶推装备上部滑移结构为研究对象,如图4-23所示。由平衡条件有:
![]()
![]()
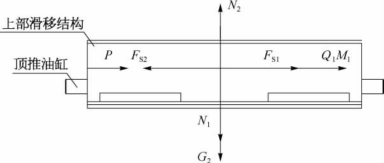
图4-23 顶推装备上部滑移结构的力学模型
以顶推装备下部支撑结构为研究对象,如图4-24所示。由平衡条件有:
![]()
![]()
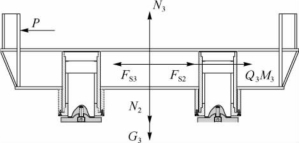
图4-24 顶推装备下部支撑结构的力学模型
由式(4-9)得,P=Fs2-Fs1-a2 M2,代入式(4-11)得:

由式(4-12)可知,支墩所需提供的水平力恰好为顶推装备启动时的加速度力。因此,在实际施工过程中,控制启动的加速度可以相应地控制支墩所需提供的原始水平力。同时,以上的推导过程证明了顶推装备的自平衡原理,即在顶推施工过程中顶推力和摩阻力转移到顶推装备内部,顶推力和摩阻力均为设备内力,支墩基本不承受水平载荷,这正好符合顶推施工支墩的受力要求。因为通常支墩为悬臂立柱结构,顶推施工过程中墩顶水平力要最大限度减小,以节省临时结构成本,增加施工安全。
在顶推施工过程中,由于支撑位置的不断变化,支墩的支撑反力不断变化,因此需要支撑反力是可控的,支墩的支反力不仅是施工过程中结构安全的控制性因素,而且是施工过程中顶推力控制的主要依据,同时也是钢箱梁局部稳定性的关键影响因素之一。由上述推导可知,在启动过程的较短时间内,不考虑支点位置的变化,影响支反力的因素是各机械结构的自身重量,这就为支墩支反力的计算提供了理论依据。
由式(4-11)可知,顶推力P=Fs2-Fs3+a3 M3,将式(4-12)代入,可知:
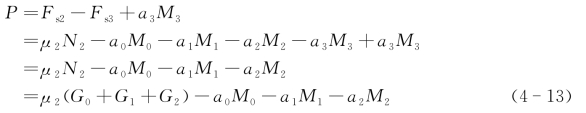
将G0=M0g,G1=M1g,G2=M2g代入得:

故顶推力P与钢箱梁、三角形楔块、上部滑移结构的质量均有关,与摩擦系数μ和加速度a有关。
为了使钢箱梁G1与顶推装备不产生相对滑动,则需要满足:
![]() (https://www.xing528.com)
(https://www.xing528.com)
由式(4-2)、式(4-3)和式(4-4)得:
![]()
故:
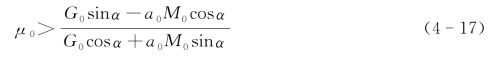
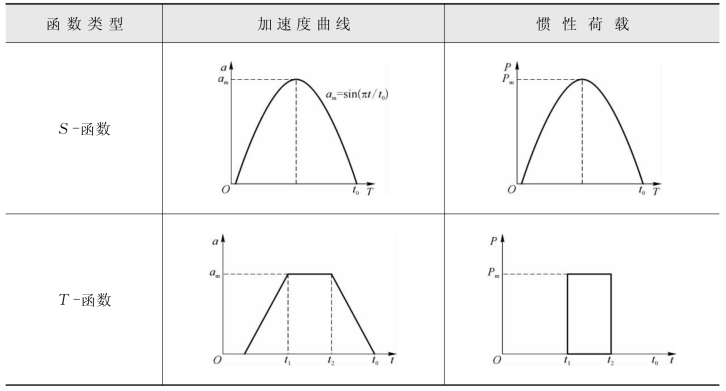
现讨论几种典型的加速度变化曲线。表4-2表明了在顶推过程中加速度与顶推力之间的关系,比较两种不同加载方式的惯性荷载可以看出,以T-函数加载时的冲击力要比在S-函数下加载的冲击力更明显。以下将对两种情况的速度和位移做进一步的分析。
表4-2 加速度与惯性荷载曲线
设![]() ,则:
,则:
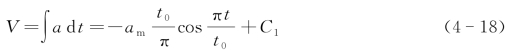

由边界条件可知,t=0时,X=0,代入式(4-19)得到:)
![]()
设油缸最大行程为d,t=t0时,X=d,代入式(4-18)得到:)
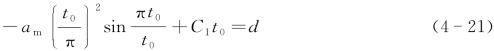

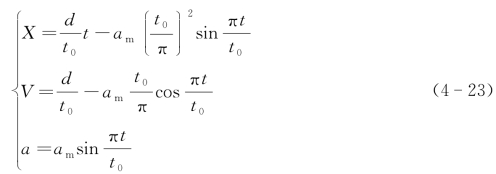
当初始t=0时,V=0,代入式(4-18)得到:


令平均速度
![]()
则有:
![]()
有
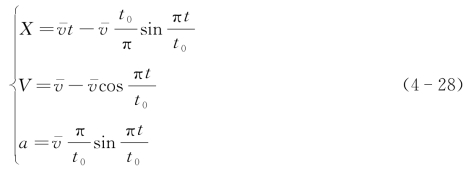
设:
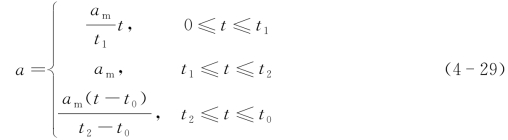
则:

由边界条件可知,t=0时,V=0,代入式(4-21)得到:
![]()
由函数的连续性可知:
当t=t1时,![]() ,得:
,得:
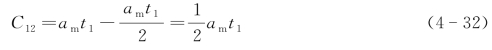
当t=t2时,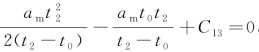 ,得:
,得:

故有:

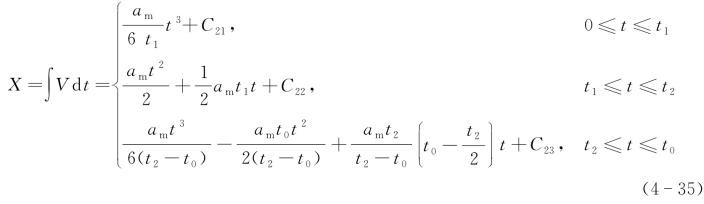
由边界条件可知,t=0时,X=0,代入式(4-35)得到:
![]()
由函数的连续性可知:
当t=t1时, ,得:
,得:
![]()
当t=t2时,
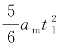 ,可得:
,可得:
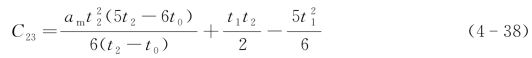
根据以上两种不同加载方式下加速度、速度和位移的变化,可以依据以上理论分析,在施工过程中以不同方法施加的启动顶推力对设备的影响来确定其水平力,为顶推施工提供了理论依据。
通过对多点同步顶推施工的力学分析,可以得到以下结论:
(1)支墩所需提供的水平力恰好为顶推装备启动时的加速度力,因此在实际施工过程中,控制启动的加速度可以相应地控制支墩所需提供的原始水平力。
(2)顶推装备具备自平衡体系,即在顶推施工过程中顶推力和摩阻力转移到顶推装备内部,顶推力和摩阻力均为设备内力,支墩基本不承受水平载荷,这正好符合顶推施工支墩的受力要求。
(3)在启动过程的较短时间内,不考虑支点位置的变化,影响支反力的因素是各机械结构的自身重量,为支墩支反力的计算提供了理论依据。
(4)在顶推过程中加速度与顶推力之间存在一定的关系,通过这种关系,可以采用不同的方式施加顶推力从而对机械结构的受力产生影响,指导实践。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




