液压系统可靠性分析基础理论

1）可靠性定义 可靠性是指产品在规定的条件下和规定的时间内，完成规定功能的能力。这个定义有四个要点：

（1）产品。定义中的产品是广义的，包括零（元）件、整机、设备、系统等。系统的概念是相对的，可大可小。

（2）规定的条件。它是指产品在使用过程中的各种条件，包括环境、运输、保管、操作技术条件等。这些条件会对产品的寿命和功能产生很大的影响。

（3）规定的时间。它是指产品的预期寿命。可靠性中的一个重要问题就是时间因素，产品的功能只有与对应的使用时间相联系，才有实际意义。而产品又只能在一定的时间内发挥其作用，不可能永远保持其使用功能不变。

（4）规定功能的能力。产品可靠是指其在实际使用中能够实现其规定的功能，产品丧失功能则称之为失效，也称为故障。

2）可靠性的特征量 可靠性的特征量是指在对产品进行可靠性研究时的一个评价标准，即用来评判什么样的产品可靠度高，什么样的产品可靠度低的一个指标。

不同产品的性能不同，因此不能用同一个指标来评价产品可靠性的高低。日常使用中，人们往往关心的是产品的使用寿命和出现故障的概率，因此常用的可靠性评价标准有：平均寿命、可靠度、失效率、可靠寿命等可靠性寿命指标，以及维修度、修复率和重要度等。

（1）可靠度与不可靠度。产品的可靠度指产品在规定的条件和规定的时间内完成规定功能的概率，记为R（t），是一个随时间变化的函数。相反，不能按时完成规定功能的概率则称为不可靠度，记为F（t）。

式中 　T——产品的寿命，是一个随机变量；

t——规定的时间。

以液压系统为例，现详细分析可靠度的定义。“规定的条件”是指液压元件工作的环境和外负载条件，不同的使用条件，同一液压元件的可靠度也不一样。“规定的时间”是指液压系统在设计完成后，能够可靠工作的时间年限。“规定的功能”是指液压元器件在正常使用过程中，能够达到的规定功能和技术参数。

（2）故障概率密度函数。故障概率密度函数f（t）是不可靠度函数的导数，其数学表达式为：

设系统中元件的总数目为N，从开始工作到时刻t，产品出现故障的个数为n（t），到t＋Δt时刻，产品出现故障的个数n（t＋Δt）。当N足够大时，则：

故障概率密度函数的定义是：在任意时刻t，产品总数目中下一个单位时间内发生故障的概率。

（3）失效率。失效率又称为故障率，是指某机械产品工作到t时刻还没有发生故障，在t时刻以后的单位时间Δt里发生故障的比率。失效率也是一个随时间变化的函数，记为λ（t），其数学表达式为：

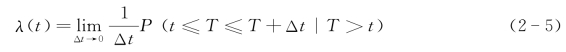
当单位时间Δt→0时，

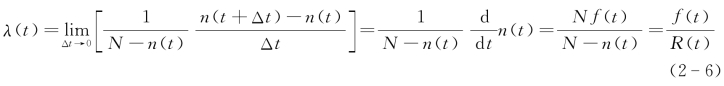
以上三式表明，产品的可靠度R（t）、不可靠度F（t）、故障概率密度f（t）、失效率λ（t）之间相互联系，若已知其中之一，便可求解得到其余三个指标。

失效率曲线表示了机械产品总体在规定寿命期内出现故障的情况。机械产品的可靠性取决于产品的故障概率，而机械产品的故障概率会随着使用时间的变化而变化，依据相关理论分析与数据计算，得出产品的失效率曲线形状如图2-33所示，它分为三段，分别对应产品的三个不同时期。

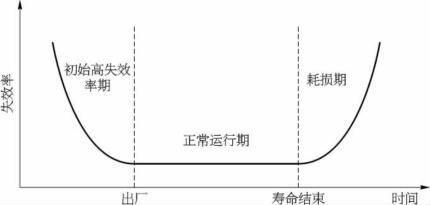
图2-33　失效率曲线（浴盆曲线）

初始失效期一般为产品的试车跑合阶段。在这一阶段，失效率会从开始很高的数值急剧下降到某一个稳定的数值。为了提高这一阶段的可靠性，产品在出厂前需要进行严格的调试，并采取一定的措施降低失效率。

正常运行期也即为产品的有效寿命期。在此阶段如果发生失效，都是由偶然原因引起的，其失效的特点是随机性的。这一阶段的失效率低且稳定，近似为常数，产品、系统的可靠度通常以这一时期为代表。可以进一步通过提高产品可靠性设计质量，改进设备管理，加强监控诊断等工作来降低产品的失效率，延长产品的使用寿命。

耗损期出现在产品使用的后期，其随着工作时间的增加而上升。耗损失效主要是因为产品经过长时间使用后会发生疲劳、磨损、老化等现象，进而会频繁地失效，使失效率随时间推移越来越高，最终将会导致产品的功能丧失。

对于失效率曲线变化的三个阶段，应尽可能降低失效率，以延长产品的使用寿命。

（4）平均寿命。平均寿命指的是机械产品寿命的平均值。对于故障发生后不可以修复，只能进行更换的机械产品，是指其故障前的工作时间，即平均无故障工作时间，记做MTTF（Mean Time To Failure）；而对故障发生后可以修复继续使用的机械产品，指的是它的无故障工作时间，即平均故障间隔时间，记做MTBF（Mean Time Between Failure）。

3）系统可靠性的常用概率分布(www.xing528.com)

（1）指数分布。指数分布在可靠性工程中，特别是在电子元件的可靠性研究方面，是最基本、最常用的失效分布形式。偶然发生的事件、偶然故障经常将失效分布函数假设为指数分布。指数分布的重要性质是无记忆性，当产品寿命T服从失效率为λ的指数分布时，可求出指数分布场合下的可靠性指标特征量如下所示：

式中　R（t）——可靠度；

f（t）——故障概率密度函数；

MTBF——平均寿命。

上述的可靠度特征量中，可靠度、不可靠度、失效率和故障概率密度函数是可靠性评价中最基本的四个特征量，它们之间的联系密切，知道其中一个，就可以求出其他所有指标。它们之间的关系如图2-34所示。

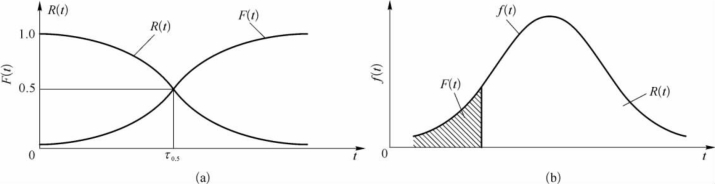
图2-34　可靠度、失效率与时间的关系

（2）正态分布。正太分布是应用比较广泛的分布，自然界中许多现象都服从正太分布，它能够很好地描述比较集中的故障现象，如液压系统中由于磨损、腐蚀、疲劳引起故障的产品寿命分布。当产品的寿命服从正太分布时，即N（μ，θ2），其特征量表达式如下：

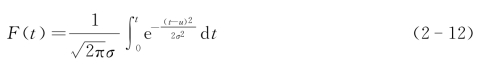
式中　t——产品寿命；

μ——产品寿命的期望值；

σ——标准差；

f（t）——密度函数；

R（t）——可靠度函数；

F（t）——不可靠度函数。

（3）威布尔分布。威布尔分布是瑞典科学家威布尔在计算链的强度时提出来的，是一种比较复杂的分布形式，因其能较好地描述机电类产品的磨损累计故障分布，所以在可靠性工程中被广泛地应用。威布尔分布下可靠性指标的特征量如下所示：

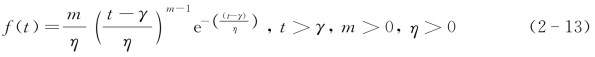
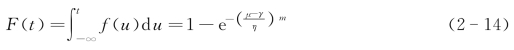
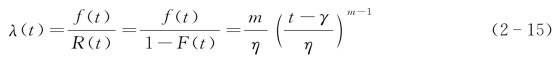
式中　m——形状参数；

η——尺度参数；

γ——位置参数；

f（t）——分布函数；

F（t）——不可靠度函数；

λ（t）——故障率函数。

由于液压故障率遵循“浴盆曲线”，不难发现：指数分布规律比较符合正常运行期的情况，正态分布规律比较符合耗损故障期的情况，而威布尔分布，当它的形状参数m＜1时，符合初始故障期的情况；m＝1时，与正常运行期情况相对应；m＞1时，又对应于耗损故障期情况，因此威布尔分布应用范围最广。