地下水运动与完整集水井的稳定性

1863 年法国水力学家裘布依（J.Dupuit）首先应用线性渗透定律，导出了著名的完整井稳定流的涌水量方程式——裘布依公式。裘布依假设抽水井布置在均质等厚、分布宽广、隔水底板水平（若为承压水则顶板也是水平）的含水层中央，抽水前地下水面是静止的水平面，地下水运动符合达西定律，并处于稳定流的条件下，呈层流运动的缓变流。

1.地下水向潜水完整井的稳定运动

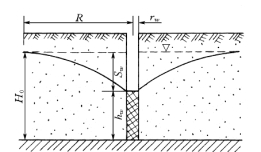
图4-12　地下水向潜水完整井的稳定流动

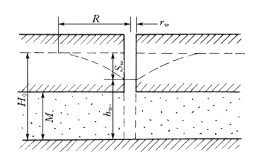
从潜水含水层中抽水时，随着井内水位降低，含水层中的水从井壁流向井内，水井周围的潜水面也随之降低，距抽水井越远，水位下降值越小，到一定远处水位降深等于零。这样潜水面就形成了以抽水井为中心的漏斗状曲面，这个漏斗状曲面称为降落漏斗，如图4-12 所示。在抽水过程中，降落漏斗不断扩大，当井中涌水量和动水位稳定一段时间后，降落漏斗趋于稳定，井内水位也相应在某个高度上稳定下来。此时从井内抽出的水量与流入井中的水量相等，并为定值，属稳定流。从降落漏斗边缘到抽水井中心的距离称为影响半径R。

取隔水底板井径方向为r轴，井轴方向为H轴（图4-12），距井轴r处任一过水断面面积为A（该处过水断面高度为H），水力坡度为i，则

根据达西定律，可写出如下涌水量方程式：

上式为一阶常微分方程，可用分离变量积分求解。其边界条件为：r＝rw时，H＝hw；r＝R时，H＝H0，将此代入式（4-6）后得

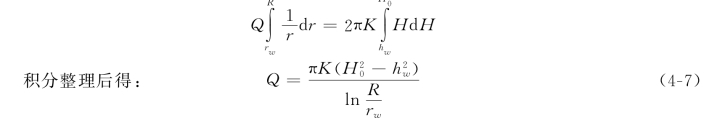
式（4-7）即为地下水向潜水完整井稳定运动的裘布依公式。

将自然对数换为常用对数，并用Sw 代表井中水位降深，即Sw＝H0－hw，则式（4-7）可写成如下形式：

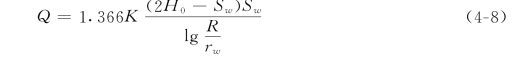
若涌水量和水位降深已知，根据式（4-8）可导出渗透系数K的计算公式：

若含水层渗透系数和涌水量已知，根据式（4-8）可导出水位降深计算公式：

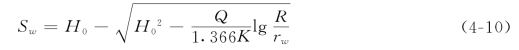
当抽水井附近有一或二个观测孔时，改变积分上、下限，可得下列涌水量公式：

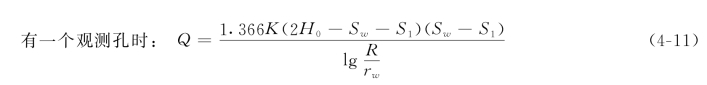
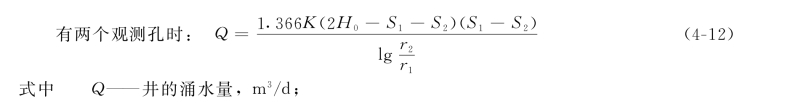
K——含水层渗透系数，m／d；

H0——潜水含水层厚度，m；

hw——抽水井动水位（从隔水底板算起），m；

Sw——抽水井水位降深，m；

S1、S2——距抽水井r1、r2 处观测孔1、2 的水位降深，m；

rw——抽水井半径，m；

R——影响半径，m。

2.地下水向承压完整井的稳定运动

根据达西定律，同样可以推导出承压完整井的涌水量公式（图4-13）。距井轴r处任一过水断面面积为A和水力坡度为i，则

(www.xing528.com)

图4-13　地下水向承压完整井的稳定流动

根据达西定律，可写出如下涌水量方程式：

边界条件为：当r＝rw 时，H＝hw；r＝R时，H＝H0，分离变量积分后得：

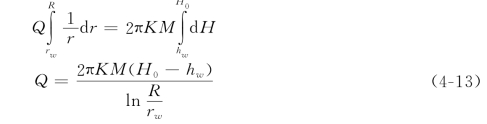
将自然对数换为常用对数，并用Sw 表示井中水位降深，则涌水量公式为

当抽水井附近有一或二个观测孔时，涌水量公式分别为

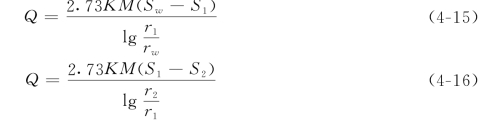
式中M——承压含水层厚度，m；

其余符号代表意义同前。

3.关于裘布依公式的几点说明

（1）影响半径R 影响半径是稳定流理论的一个重要的水文地质参数，可用经验公式计算其近似值。

潜水含水层可用库萨金公式：

承压含水层可用吉哈尔特公式：

式中渗透系数K以m／d为单位，含水层厚度H0 和水位降深Sw 以m为单位。

实际工作中，常用多孔抽水试验资料确定影响半径。如在一个抽水井中抽水，在其周围布置一定数量的观测孔，观测其水位下降值，然后利用裘布依公式计算R。采用两个观测孔的资料时：

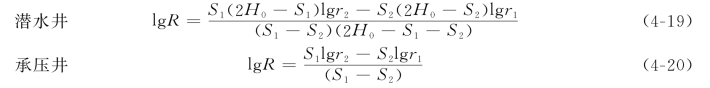
（2）水位降深用裘布依公式计算井内水位降深Sw比实测值常偏小，这是因为抽水时地下水向井内运动需要一定水位差，故井内水位要比井壁外水位低，这种现象称为水跃。裘布依公式没有考虑水跃值。为了精确计算井内水位降深或降落曲线，必须考虑水跃问题。阿勃拉莫夫提出计算水跃值的经验公式如下：

式中Δh——水跃值，即抽水时井管内外的水位差，m；

Q——涌水量，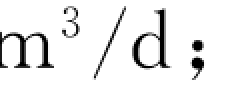

Sw——井内水位降深，m；

K——渗透系数，m／d；

F——过滤器工作面积，F＝πdL，其中d为过滤器直径，L为过滤器有效长度；

a——经验系数，取决于过滤器的结构。网状或砾石过滤器，a＝15～25；穿孔、缠丝及金属过滤器，a＝6～8。

（3）涌水量从裘布依公式可以看出，涌水量与水位降深成正比，但实际情况并不是水位降深越大，涌水量也越大。只有当水位降深不大或降落漏斗曲线坡度小于15°时，该公式计算结果才符合实际。所以，用公式计算井的最大涌水量时，水位降深Sw宜不大于（1／3～1／2）潜水含水层厚度或承压水井中水柱高度H0。