混凝土和砌体结构承重纵墙计算

1）单层刚性方案房屋承重纵墙的计算

（1）计算单元

当单层房屋静力分析属于刚性方案时，承重纵墙一般取相当于一个开间宽度的有代表性的墙体作为计算单元（图19-12）。

（2）计算简图

计算时可采用下列假定：

①纵墙、柱下端在基础顶面处固接，上端与屋盖大梁（或屋架）铰接。

②屋盖结构可作为纵墙、柱上端的不动铰支座。

于是，可得纵墙、柱的计算简图如图19-13所示。

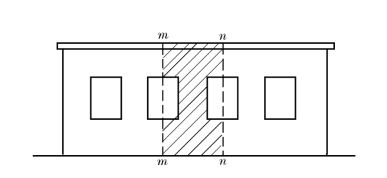
图19-12 单层房屋承重纵墙的计算单元

图19-13 单层刚性方案承重纵墙的计算简图

（3）荷载和内力

作用在纵墙上的荷载及其所引起的内力如下：

①屋盖荷载

屋盖荷载包括屋盖恒荷载及屋面活荷载（屋面均布活荷载或雪荷载）。屋面荷载通过屋架或屋面大梁以集中力Q1 作用于纵墙顶部。当采用屋架时，Q1 位于屋架下弦端部节点中心处，一般距墙定位轴线150mm；当采用屋面梁时，Q1 距墙内边缘的距离为0.4a0，a0 为梁端有效支承长度，于是作用于纵墙顶部的荷载Q1 对墙体的偏心距e1 即可求得。因而，作用于纵墙顶部的荷载除有轴心压力Q1 外，还有弯矩M=Q1e1。墙体内力如图19-14所示。

图19-14 屋面竖向荷载作用下的内力图

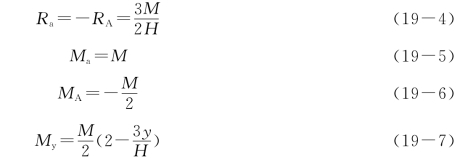
②风荷载

作用在单层房屋纵墙上的风荷载包括作用于墙面上和屋面上的风荷载（包括作用于女儿墙上的风荷载）。作用于屋面上的风荷载可简化为作用于墙顶的集中力Qw，它直接通过屋盖传给横墙，由横墙传至基础，再传给地基，对纵墙不产生作用。作用于纵墙面上的风荷载为均布面荷载，可简化为沿墙高度方向的均布线荷载计算（图19-15）。在均布线荷载q作用下，等截面墙体的内力如图19-15所示。

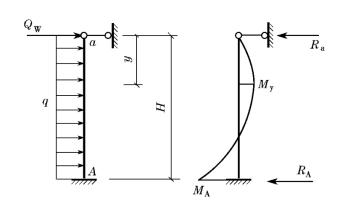
图19-15 风荷载作用下的内力图

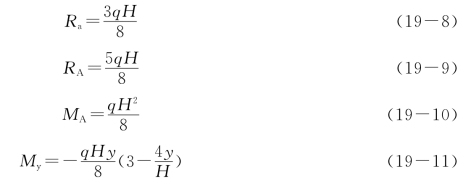
当时，弯矩最大，。

③墙体自重

墙体自重作用于墙体截面重心处，按砌体的实际重量计算。当墙体为等截面时，只引起轴力，不产生弯矩。若墙体为变截面时，上阶柱（墙）重量G1 对下阶柱（墙）的截面将产生弯矩M=G1e1，e1 为上下阶柱（墙）轴线间的距离。其内力按上端自由、下端固定的悬臂构件计算（因自重是在屋架未架设之前就已存在，故按悬壁构件计算）。

（3）控制截面与内力组合

单层房屋承重纵墙一般取Ⅰ-Ⅰ、Ⅱ-Ⅱ、Ⅲ-Ⅲ截面为控制截面（图19-13）。Ⅰ-Ⅰ为梁下截面，此处弯矩M 较大，既要按偏心受压计算墙体承载力，又要验算梁下砌体局部受压承载力。Ⅱ-Ⅱ截面为风荷载作用下的最大弯矩截面，该截面有可能起控制作用，应根据相应的M 和N 进行承载力验算。Ⅲ-Ⅲ截面为底部截面，此处受有最大的轴向力和相应的弯矩，需按偏心受压进行承载力验算。在进行承载力验算时，除局部受压外，截面面积均取窗间墙的截面面积。

控制截面确定以后，应当先求出各种荷载单独作用时控制截面的内力值，然后根据使用中可能同时作用的荷载所产生的内力值进行组合，求出不利内力，再进行截面验算。

一般采用以下三种荷载组合：

（1）恒荷载+风荷载。

（2）恒荷载+屋面活荷载。

（3）恒荷载+0.9（屋面活荷载+风荷载）。

注意：风荷载分左风和右风，应取不利情况。

2）多层刚性方案房屋承重纵墙的计算

（1）计算单元

多层房屋一般是取相邻两侧各1／2开间，即（s1+s2）／2宽的墙段（s1、s2 为有代表性的相邻两开间的宽度）作为计算单元（图19-16）。计算截面面积A，当有门窗洞口时，取窗间墙的截面面积。如无门窗洞时，则取计算单元墙体的截面面积。对于带壁柱墙，当无门窗洞口时，计算截面宽度应取下述二者中的较小值。

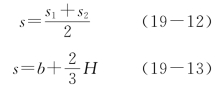
式中 b——壁柱宽度；

H——楼层高度。

当有门窗洞口时，可取窗间墙宽度。

（2）计算简图和内力计算

多层刚性方案房屋承受的荷载有竖向荷载和水平荷载（一般为风荷载）。

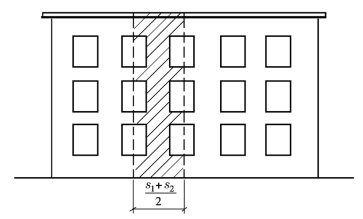
图19-16 多层房屋承重纵墙的计算单元

①竖向荷载作用下

在竖向荷载作用下，墙体在屋盖和楼盖处的截面所能传递的弯矩很小，其原因是由于梁、板的支承长度往往比较长，使得墙体的连续性遭到削弱。为简化计算，假定墙体在屋盖和楼盖处为铰接。在基础顶面上，对多层房屋来说，轴向力起主导作用，弯矩相对较小，考虑弯矩作用与否对此处截面的承载力影响不大，也假定墙体与基础为铰接（注意：单层房屋不能采用这种假定）。因此，在竖向荷载作用下，墙、柱在每层高度范围内（底层取底层层高加室内地面至基础顶面的高度），可近似视作两端铰支的竖向受压构件（图19-17a）。对本层楼盖传来的荷载，应考虑梁、板对墙、柱的实际偏心影响。梁端支承压力Nl 到墙内边的距离，应取0.40a0。a0 为梁端有效支承长度，按公式（18-13）计算。由上部墙体传来的荷载Nu，可视为作用于上一楼层墙、柱的截面重心处。(www.xing528.com)

按照上述假定，上下层墙体在楼盖支承处均为铰接，则在计算某层墙体时，以上各层荷载传至该层墙体顶端支承截面处的弯矩为零。在所计算层墙体顶端截面处，由楼盖传来的竖向力，则按其实际偏心距作用着。实践证明，这种假定既偏于安全，又基本符合实际。

现以图19-17所示三层楼房的第二层和第一层砖墙为例，来说明其内力的计算方法。

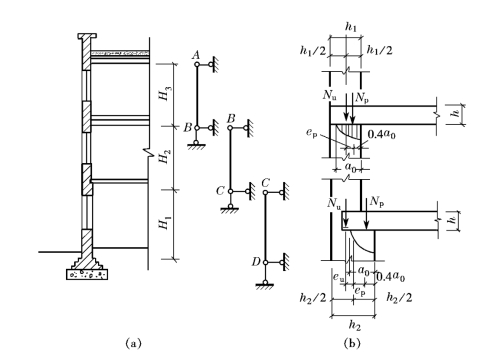
图19-17 多层刚性方案承重纵墙的计算简图

对第二层墙，其计算简图和内力如图19-18a所示。

图19-18 刚性方案多层房屋纵墙的计算简图和内力图

上端截面（Ⅰ-Ⅰ）

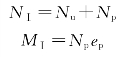
下端截面（Ⅱ-Ⅱ）

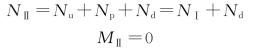
对底层墙，假定墙体在一侧加厚，则由于上下层墙厚不同，上下层墙轴线偏离eu。因此，由上层墙传来的竖向荷载Nu 将对下层墙产生弯矩（图19-18b），其计算简图和内力如图19-18所示。

上端截面（Ⅰ-Ⅰ）

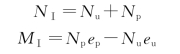
下端截面（Ⅱ-Ⅱ）

式中 Np——本层墙顶楼盖的梁或板传来的荷载设计值；

ep——Np 对墙体截面重心线的偏心距；

Nu——由上层传来的荷载设计值；

eu——Nu 对本层墙体截面重心线的偏心距；

Nd——本层墙体自重（包括内外粉刷和门窗自重等）设计值。

Np 对本层墙的偏心距ep 可按下列公式计算：

式中 y——墙截面重心到受压最大边缘的距离，对矩形截面墙体，，h为墙厚。

当墙体在一侧加厚时，上下墙重心线间的距离eu 按下列公式计算

式中 h1、h2——上、下墙体的厚度。

对于梁跨度大于9m 的墙承重的多层房屋，按上述方法计算时，应考虑梁端约束弯矩的影响。可按梁两端固结计算梁端弯矩，再将其乘以修正系数γ后，按墙体线性刚度分到上层墙底部和下层墙顶部，修正系数γ可按下式计算：

式中 a——梁端实际支承长度；

h——支承墙体的墙厚，当上下墙厚不同时取下部墙厚，当有壁柱时取hT。

②水平荷载作用下

在水平荷载作用下，墙体可视为一个竖向连续梁。为了简化起见，该连续梁在风荷载作用下的弯矩值可近似地取

式中 w——计算单元每米高墙体上的风荷载设计值；

H——层高。

计算时应考虑两种风向，而所采用的风向（迎风和背风面）应使竖向荷载算得的弯矩在该截面组合后的代数和增加，而不是减少。

对于刚性方案多层房屋的外墙，当洞口水平截面面积不超过全截面的2／3，房屋的层高和总高不超过表19-5的规定，且屋面的自重不小于0.8kN／m2 时，可不考虑风荷载的影响，仅按竖向荷载进行计算。

表19-5 外墙不考虑风荷载影响时的最大高度

注：对于多层砌块房屋190mm 厚的外墙，当层高不大于2.8m，总高不大于19.6m，基本风压不大于0.7kN／m2 时可不考虑风荷载的影响。

（3）控制截面和内力组合

墙、柱的内力求出后，就要选择几个控制截面进行内力组合和偏心受压、局部受压等承载力计算。

有门窗洞口的纵墙，其计算截面取窗间墙截面。一般来说，同一计算单元每层墙的上下厚度和砂浆强度等级都是一样的，也即计算截面大小和砌体强度都相同。所以控制截面就取决于组合后内力的数值。

每层墙可取两个控制截面并作相应的简化。上截面可取墙体顶部位于大梁（或板）底的砌体截面Ⅰ-Ⅰ，该截面中弯矩M 最大，即偏心距最大，对该截面应进行偏心受压和梁下局部受压等承载力计算。下截面可取墙体下部位于大梁（或板）底稍上的砌体截面Ⅱ-Ⅱ，对于底层墙下截面应取基础顶面处墙体的截面，这些截面的N 最大，弯矩M 为零。在此假定计算截面面积按窗间墙截面面积采取，并按墙高中部截面考虑纵向弯曲的影响，即按e／h或e／hT（Ⅰ-Ⅰ截面按e／h，Ⅱ-Ⅱ截面按e／h=0）在附表32中采取φ（按理论，不动铰支座截面是不产生纵向弯曲的）。这样，每层墙的其他截面一般不起控制作用。

若几层墙体的截面和砂浆强度等级相同，则只需验算其中最下一层即可。若砂浆强度等级有变化，则开始降低砂浆强度等级这一层也应该验算。