高厚比、轴向力偏心距对受压构件承载力的影响系数

根据对试验资料的分析，《砌体规范》规定，对于无筋砌体矩形截面单向偏心受压构件，承载力影响系数φ 可按下述公式计算：

当β≤3时

当β＞3时

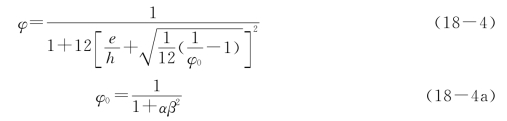
式中 e——轴向力的偏心距；

h——矩形截面的轴向力偏心方向的边长；

φ0——轴心受压构件的稳定系数；

α——与砂浆强度等级有关的系数，当砂浆强度等级大于或等于M5时，α=0.0015；

当砂浆强度等级等于M2.5时，α=0.002；当砂浆强度等于0时，α=0.009；

β——构件高厚比。

计算T 形截面受压构件的φ 时，应以折算厚度hT 代替公式（18-2）和公式（18-3）中h。按公式（18-2）和公式（18-3）计算的φ 值已列于附表32，供设计时查取。

计算影响系数φ（用公式计算或查表）时，为了考虑不同种类砌体受力性能的差异，构件高厚比应按下列公式确定：

对矩形截面

对T 形截面

式中 γβ——不同砌体材料的高厚比修正系数，按表18-1采用；

H0——受压构件的计算高度；

h——矩形截面轴向力偏心方向的边长，当轴心受压时为截面较小边长；

hT——T 形截面的折算厚度，可近似取hT=3.5i；

i——截面回转半径。

表18-1 高厚比修正系数γβ

注：对灌孔混凝土砌块砌体，γβ 取1.0。

例题18-1 截面为490mm×490mm 的砖柱，采用强度等级为MU10的烧结普通砖和M5混合砂浆砌筑。柱的高度H 和计算高度H0 为4.2m，柱顶承受轴心压力设计值N=250kN。试验算该柱的承载力。

解 该柱的控制截面在柱底。

用砂浆砌筑的机制砖砌体的重力密度为19kN／m3。

柱自重设计值 G=19×0.49×0.49×4.2×1.2=22.99≈23kN

柱底截面承受轴心压力设计值 N=250+23=273kN

当e=0时，由式（18-4）和（18-4a）得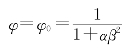

砂浆强度等级为M5时，α=0.0015

φ 值也可由附表32-1查得。

由附表27-1可得f=1.50N／mm2

故f 应乘以调整系数γa。

由公式（17-8）得 γa=0.7+A=0.7+0.24=0.94(https://www.xing528.com)

该柱承载力满足要求。

例题18-2 某建筑物底层，横墙厚240mm，采用MU15蒸压粉煤灰普通砖和M5混合砂浆砌筑，计算高度H0=3.5m，承受轴向压力设计值N=250kN／m（包括自重）。试验算该墙体的承载力。

解 取1m 宽的墙体为计算单元。

因是连续墙体，不用考虑A＜0.3m2 时对f 的修正。

由附表27-2查得f=1.83N／mm2。

该墙体承载力满足要求。

例题18-3 有一砖柱采用MU10烧结多孔砖和M5混合砂浆砌筑，截面尺寸为490mm×620mm（图18-3），M 作用方向和垂直于M 作用方向的H0 均为6.0m。承受轴向力设计值N=168kN，沿长边方向作用的弯矩设计值M=21kN·m。试验算该柱的承载力。

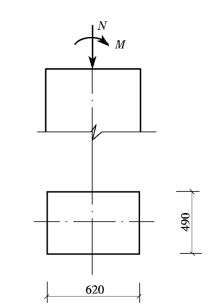
图18-3 例题18-3

解 （1）验算柱弯矩作用方向的承载力

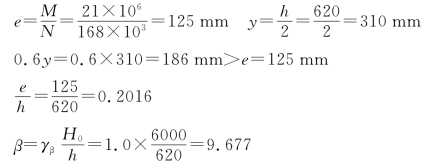
砂浆强度等级为M5时，α=0.0015。

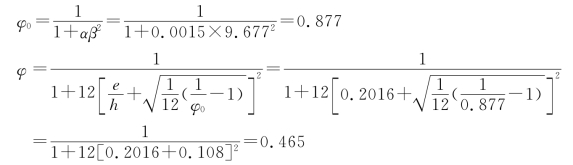
φ 值也可由附表32-1查得。

由表27-1可查得f=1.5N／mm2。

故f 不需乘调整系数γa。

承载力满足要求。

（2）验算垂直于M 作用方向的承载力

对矩形截面构件，当轴向力偏心方向的截面边长大于另一方向的边长时，除按偏心受压计算外，还应对较小边长方向按轴心受压进行验算。

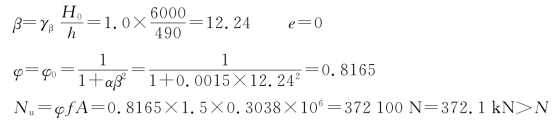
承载力满足要求。

例题18-4 某单层厂房纵墙，其窗间墙截面尺寸如图18-4所示。采用MU10烧结多孔砖和M5混合砂浆砌筑，墙的计算高度H0=6m，承受弯矩设计值M=60kN·m，轴向力设计值N=350kN。轴向力作用点位于壁柱一侧，试验算该墙的承载力。

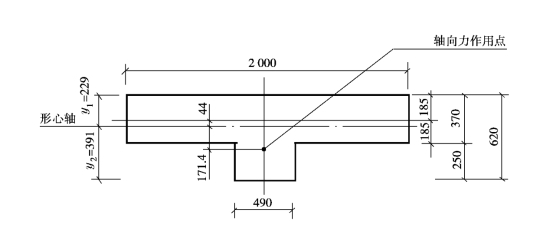
图18-4 例题18-4

解 （1）截面几何特征值

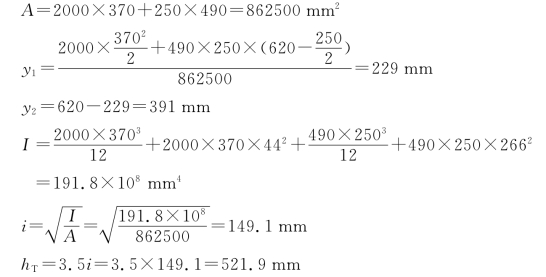
（2）承载力验算

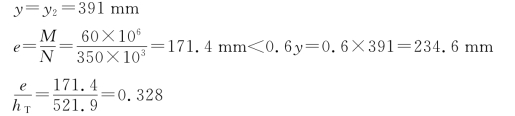
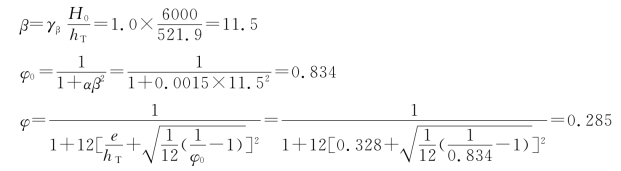
由附表27-1查得f=1.5N／mm2。

承载力满足要求。