受压构件承载力计算公式

砌体结构在房屋结构中多用于墙、柱、基础等受压构件。试验结果表明，对于短粗的受压构件，当构件承受轴心压力时，从加荷到破坏，构件截面上的应力分布可视为均匀的（图18-1a），破坏时截面所能承受的压应力可达到砌体的抗压强度，但是对于承受偏心压力的构件和高厚比较大的细长构件来说，其承载能力都将下降，其主要原因如下：

（1）构件承受偏心压力时，截面中的应力分布不均匀，由于砌体的弹塑性性能，使应力呈曲线分布（图18-1b）。随着偏心距的增大，在远离轴向力作用一侧的截面中将出现拉应力。当受拉边缘的应力达砌体沿通缝截面的弯曲抗拉强度时，砌体将产生水平裂缝（图18-1c），裂缝不断向轴向力偏心方向延伸（图18-1d），致使截面的受压面积随之减小，承载力下降。纵向力的偏心距愈大，承载力降低愈多。

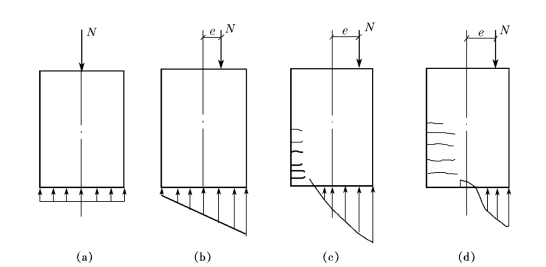
图18-1 受压构件截面上的应力分布

（2）对于承受轴心压力的细长构件，由于砌体材料的不均匀性和施工质量的影响，轴向力作用线不可能完全与构件的纵轴线相重合，因而使构件的侧向变形增大，稳定性降低。对承受偏心压力的细长构件，随着受压面积的减小，构件的稳定性随之削弱。侧向变形增大后，引起附加偏心距，使荷载的偏心距加大，结果又增大了构件的侧向挠曲，致使构件稳定性继续降低（图18-2）。这样的相互作用加剧了柱的破坏，大大降低了构件的承载力。

在砌体结构中，构件的长细比常用高厚比来表示。高厚比是指墙、柱的计算高度H0 与墙厚或柱边长h的比值。

基于上述原因，对构件进行承载力计算时，应当考虑高厚比和偏心距对承载力的影响。

综合以上分析，受压构件的承载力可按下式计算：

式中 N——轴向力设计值；

φ——高厚比β和轴向力的偏心距e 对受压构件承载力的影响系数，可按公式（18-3）和公式（18-4）计算或按附表32查用；(www.xing528.com)

f——砌体抗压强度设计值，按附表27选用；

A——构件截面面积，对各类砌体均可按毛截面计算。

计算构件截面面积时，对带壁柱墙，其翼缘宽度bf 可按下列规定采用：对多层房屋，当有门窗洞口时，可取窗间墙宽度；当无门窗洞口时，每侧翼墙宽度可取壁柱高度的1／3；对单层房屋，可取壁柱宽加2／3墙高，但不大于窗间墙宽度和相邻壁柱间距离。

由于偏心距较大时，很容易在截面远离轴向力一侧受拉区产生水平裂缝，而且裂缝开展较大，使得截面受压区的面积减小较多，构件刚度明显减小。此时纵向弯曲的不利影响增大，构件的承载力明显下降。因此《砌体规范》规定，按内力设计值计算的轴向力偏心距e不应超过0.6y，即

式中 y——截面重心到轴向力所在偏心方向截面边缘的距离。

必须指出，对矩形截面构件，当轴向力偏心方向的截面边长大于另一方向的边长时，除按偏心受压计算外，还应对较小边长方向按轴心受压进行验算。此时应按短边边长计算β，并取e=0，φ=φ0，φ0 可按式（18-4a）计算，也可从附表32中的栏内查出。

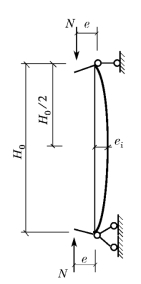
图18-2 偏心受压构件的附加偏心距