混凝土结构与砌体结构：十字交叉条形基础的计算和构造

十字交叉条形基础为具有较大抗弯刚度的高次超静定结构体系，对地基的不均匀变形有较大的调节作用，因此十字交叉条形基础在一般工业与民用多、高层建筑中应用较为广泛。

1）十字交叉条形基础的内力计算

十字交叉条形基础的内力计算较为复杂。较常采用的计算方法有节点荷载分配法和有限元法等。工程设计中，一般采用节点荷载分配法。当十字交叉条形基础的布置复杂、不规则或欲获得精度较高的计算结果时，宜采用有限元法。下面主要介绍节点荷载分配法。

如图15-69所示，在十字交叉条形基础的每个节点上作用着集中荷载Fi 和分别沿x、y 方向作用的弯矩Mix、Miy，欲求其内力，必须先将集中荷载在纵、横向梁上进行分配。

图15-69 十字交叉条形基础节点受力简图

（1）基本方程

为简化计算，可忽略基础扭转变形的影响，假定在十字交叉点处纵横两方向的基础梁是上下铰接的，即作用于基础纵向平面内的力矩Mix全部由纵向基础梁承担，作用于基础横向平面内的力矩Miy全部由横向基础梁承担。因此，根据节点i处的静力平衡条件及变形协调条件可得下列方程：

式中 Fix、Fiy——分别为纵向基础梁和横向基础梁在节点i处所分担的竖向集中力；

δijx——由同一根纵向基础梁上的节点j处作用单位集中力在节点i 处所产生的沉降；

——由同一根纵向基础梁上的节点j处作用单位力矩在节点i处所产生的沉降；

δiky——由同一根横向基础梁上的节点k处作用单位集中力在节点i 处所产生的沉降；

——由同一根横向基础梁上的节点k处作用单位力矩在节点i处所产生的沉降。

由上述可见，每个节点有两个未知力Fix和Fiy，同时每个节点可列出两个方程式。若十字交叉条形基础有n个节点，则就有2n个未知数和2n 个方程式，解方程可得2n 个未知力的值。

对于十字交叉条形基础，如果结构对称、土层对称，则未知数Fix、Fiy就可大量减少。单轴对称时，只需取1／2基础进行分析；双轴对称时，只需取1／4基础进行分析。

应用上述基本方程分析基础梁内力时，必须计算有关的系数和。对于系数和的计算有多种方法。现采用地基系数法进行分析。

当按地基系数法进行计算时，考虑到集中荷载对条形基础变形的影响随距离的增大而迅速减小，因此，当节点间的间距大于1.8／λb 时，可以认为力Fi 作用处的沉降只与力Fi 有关，而与其他节点处的作用力无关。于是，基本方程及其求解将大为简化，可很简便地求得集中力分配系数。

（2）集中力分配系数

十字交叉条形基础的节点可分为内柱节点、边柱节点和角柱节点（图15-70），现将集中力分配系数分别叙述如下：

①内柱节点

内柱节点i作用着上部结构传来的集中力Fi（图15-71），Fi 可分成两个集中力Fix 和Fiy，分别作用在纵、横两向条形基础上。把纵、横两方向的条形基础都视作无限长梁，按节点i处的静力平衡条件及变形协调条件有

图15-70 十字交叉条形基础示意图

图15-71 十字交叉条形基础内柱节点i

于是得

式中 λbx、λby——分别为纵向（x 向）和横向（y 向）基础梁的柔度特征值，，；(www.xing528.com)

Ix、Iy——分别为纵、横向基础梁的截面惯性矩；

bbx、bby——分别为纵、横向基础梁的翼板宽度。

②边柱节点

边柱节点又分为两种情况（图15-72）。第一种边柱节点如图15-72a所示，该节点承受Fj 的作用，Fj 可分解为作用于无限长梁的Fjx和作用于半无限长梁上的Fjy，与中柱节点相类似，根据静力平衡条件与变形协调条件可求得

图15-72 十字交叉条形基础边柱节点j

第二种边柱节点如图15-72b所示，同理可求得

式中 ψs——与cyλby有关的系数，可由表15-22查得，此处，cy 为沿y 方向基础梁悬伸段长度（梁端至沿x 方向基础梁轴线的距离）。

表15-22 ψs 与ψc 值

注：表中的cλb，应根据计算节点的情况，取cxλbx或cyλby。

③角柱节点

角柱节点k有三种情况。对于第一种角柱节点（图15-73a），同理得

对于第二种角柱节点（图15-74b），一般取cx=（0.6～0.75）／λbx，同理可得

式中 ψc——与cxλbx有关的系数，可由表15-22查得，此处cx 为沿x 方向基础梁悬伸段长度（梁端至沿y 方向基础梁轴线的距离）。

图15-73 十字交叉条形基础角柱节点k

对于第三种角柱节点（图15-73c），当cx=（0.6～0.75）／λbx，cy=（0.6～0.75）／λby时，则可得

当十字交叉条形基础各节点的荷载分配完毕后，即可分别按条形基础求地基反力及其内力。

2）十字交叉条形基础的构造要求

十字交叉条形基础的主梁布置方向一般与上部结构的主梁设置方向一致，以增加主要承重结构平面内的整体刚度，减少基础不均匀沉降。十字交叉条形基础梁的交叉节点处构造较复杂，应注意纵、横梁与柱中三个方向上主筋设置的实际可能性和合理性。纵向与横向基础梁交叉处翼板受力钢筋配置方式如图15-74所示。翼板下的地基土如有可能与翼板脱开时，应在翼板上部设置受力钢筋。此外，基础梁的构造尚应符合15.3.2节所述的要求。

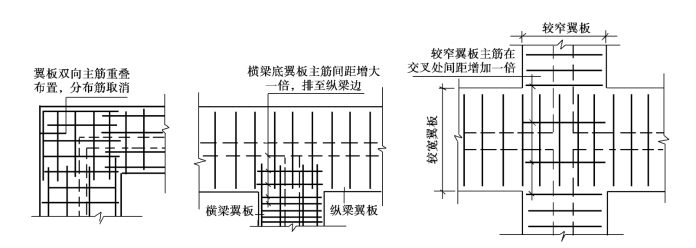
图15-74 翼板交叉处主筋布置

当考虑基础梁的受扭作用时，应按弯、剪、扭构件进行设计。