柱下条形基础计算与构造混凝土结构与砌体结构·第4版

1）条形基础的内力计算

条形基础既承受上部结构传来的荷载，又承受地基土的反力。然而，地基土的反力分布规律和大小不仅与荷载有关，而且与上部结构的刚度、条形基础的刚度和地基土的物理力学性能有关。因此，如何确定地基土的反力是求解条形基础内力的关键。在比较均匀的地基上，上部结构刚度较好，荷载分布较均匀，且条形基础梁的高度不小于1／6柱距时，地基反力可按直线分布，条形基础梁的内力可按连续梁计算，此时边跨跨中弯矩及第一内支座的弯矩宜乘以1.2的系数。不满足上述要求时，宜按弹性地基梁计算。为了确定条形基础地基上的反力，目前有多种不同的假设和计算方法，如静定分析法、倒梁法和地基系数法。现简要介绍如下。

（1）静定分析法

静定分析法假定土反力是线性分布的，同时假定上部结构为柔性的，只起传递荷载的作用。于是，经过对上部结构分析得到作用于条形基础的荷载后，即可由静力平衡条件求出土反力的最大值和最小值（图15-63）。

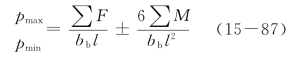
式中 ∑F——上部结构传至基础梁顶面的竖向荷载（不包括基础自重和覆土重）设计值的总和；

∑M ——上部结构传至基础梁顶面的竖向荷载（不包括基础自重和覆土重）对基底形心的力矩设计值的总和；

bb、l——分别为基础的宽度和长度。

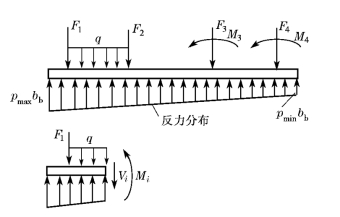
图15-63 静定分析法示意图

由式（15-87）求得基底土反力后，便可按静力平衡条件计算出基础任一截面上的内力（弯矩Mi 和剪力Vi）。

（2）倒梁法

倒梁法假定土反力呈线性分布（这与静定分析法相同），同时假定上部结构为绝对刚性，不仅起传递荷载的作用，而且作为基础梁的不动铰支座（这与静定分析法不同）。因此，可将基础梁视作铰支于柱端的倒置的多跨连续梁。于是，在按静力平衡条件求出土反力后，即可将土反力作为作用在基础梁的荷载，按多跨连续梁计算基础梁任一截面的内力，如图15-64所示。

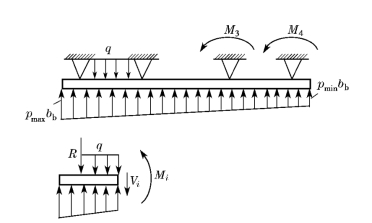
图15-64 倒梁法示意图

显然，按上述方法求得的支座反力一般不等于上部柱传来的竖向荷载，其差值称为不平衡力。为解决这个矛盾，可通过对土反力进行局部调整的方法予以修正。具体调整方法如下：将支座反力与柱荷载的差值均匀分布在该支座两侧各1／3跨度内，作为基底反力的调整值，这时反力分布呈阶梯状，然后按连续梁重新计算，直至支座反力和柱荷载基本相同为止。

必须指出，上述两种简化方法的计算结果往往会有一定的差别，只有当倒梁法求出的支座反力未经调整就恰好与柱荷载一致时，两者的结果才会相同。在工程设计中，必要时可参考上述两种简化方法求得的内力包罗图进行截面设计。

例题15-5 图15-65a为一条形基础，柱子传来的荷载分别为FA=FE=333kN，FC=1138kN，试用倒梁法计算其内力。

解 由于该梁结构对称、荷载对称，故基底土反力均匀分布，其集度为

图15-65b为倒梁法计算简图，利用连续梁的弯矩分配法求得该基础梁的弯矩和剪力，并绘于图15-65c和图15-65d。由图15-65d可求得支座反力RA=338.24kN，RC=1127.48kN，RE=338.24kN。

按倒梁法求得的支座反力RA、RC、RE 分别与柱荷载FA、FC、FE 进行比较可知，二者之差均小于1.6%，故不进行不平衡力的调整。

（3）地基系数法

地基系数法假定基础梁底面任意点的地基反力p 与该点的地基变形（沉降）s成正比（一般称为文克尔假定），其计算模型如图15-66a所示。即

式中 p——基础底面某点的地基土反力；

k——地基系数，即基础某点产生单位沉降时作用在该点单位面积上的土反力值；

s——地基在相应点的沉降量。

由基础梁中取出微元体，其静力平衡方程为（图15-66b）

式中 V——基础梁截面剪力；

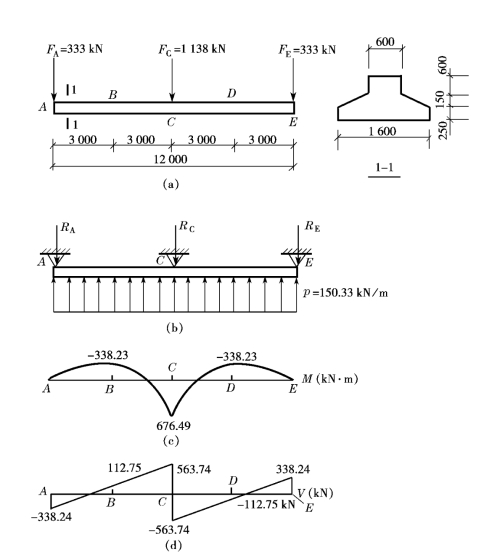
图15-65 例题15-5中的基础梁的计算简图和内力图

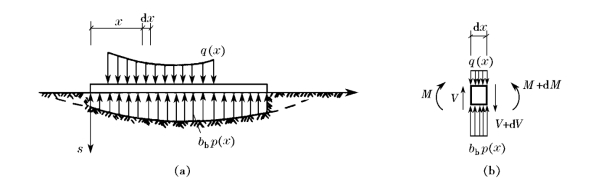
图15-66 地基系数法分析简图(www.xing528.com)

bb——基础梁底面宽度；

q（x）——上部结构传至基础梁的线荷载。

梁的挠曲微分方程为

式中 E——基础梁材料的弹性模量；

I——基础梁的截面惯性矩；

M——基础梁的截面弯矩。

因，则有，代入式（15-90）、（15-89），可得

将式（15-88）代入式（15-91），则得

令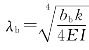，代入式（15-92），可得

式（15-93）称为弹性地基梁的挠曲微分方程，λb 称为弹性地基梁的柔度特征值。

对于无线荷载的梁段，q（x）=0，式（15-93）简化为

由上述可知，弹性地基梁挠曲微分方程为四阶常系数非齐次微分方程。

对于四阶常系数非齐次微分方程（15-93），其一般解为

其中，C1、C2、C3、C4 均为积分常数，可根据不同的边界条件确定；s0 为微分方程（15-93）的特解，由荷载条件确定，例如：当q（x）=f（x2，x2，x）时，；当q（x）=0时，s0=0，这时式（15-95）就是无线荷载梁段相应的微分方程（15-94）的通解，即

求得基础梁的挠度曲线后，由微分关系就可求得梁截面转角θ、弯矩M 和剪力V。

采用地基系数法计算条形基础，首先应确定地基系数k 值。k 的取值将影响基础的沉降，因而也将影响基础的弯矩和剪力。但是，地基系数k的取值却不易准确确定。这是因为地基系数k不但与地基土的物理力学性能有关，而且还与基础本身的尺寸、形状、刚度、荷载以及上部结构刚度等因素有关，它是一个综合的系数。读者在查阅k 值表或应用k 值计算公式时应予以注意。

2）条形基础的构造要求

条形基础的板一般在肋梁下面，因此条形基础的横截面常为倒T 形。就正截面受弯承载力而言，跨中因承受负弯矩，应按T 形截面计算；支座因承受正弯矩，应按矩形截面计算。条形基础梁的高度宜取为柱距的1／4～1／8。翼板厚度不宜小于200mm，当翼板厚度为200～250mm时，宜采取等厚度翼板（图15-67剖面Ⅰ-Ⅰ）；当翼板厚度大于250mm 时，可做成坡度i≤1∶3的变截面翼板（如图15-67剖面Ⅱ-Ⅱ所示）。当柱传来的荷载较大时，接近柱边的剪力较大，此时可在基础梁的支座处加腋（图15-67c）。条形基础梁的腹板宽度应比墙的厚度或柱在垂直于梁轴线方向的截面边长稍大些，如图15-69a所示；当腹板宽度小于柱截面边长时，则在柱子与条形基础交接处，基础应放大，其平面尺寸不应小于图15-68b的要求。一般情况下，条形基础的端部应向外伸出，其长度宜为第一跨距的0.25倍，以增大基础底面积，减小基底反力，并尽可能使合力点与基础底面形心位置重合或接近，使沿整个梁长的反力分布比较合理（图15-67），并使基础梁第一跨的跨中弯矩与支座弯矩绝对值较为接近，截面配筋更为合理。

条形基础混凝土强度等级可采用C20，素混凝土垫层厚度宜为100mm，强度等级宜为C10。

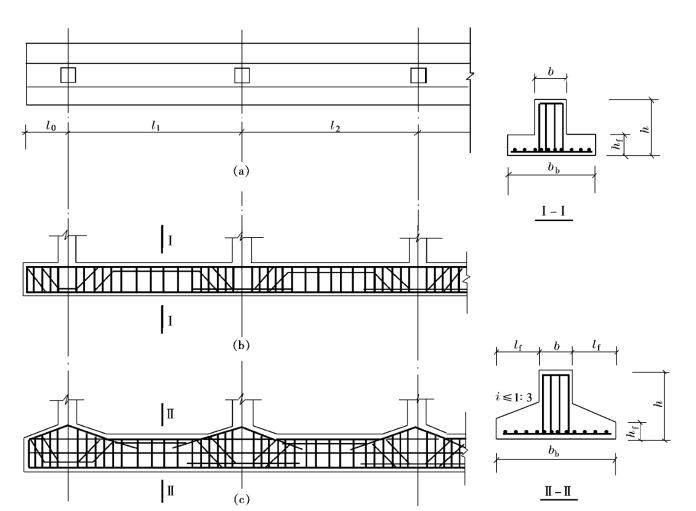
图15-67 条形基础的构造

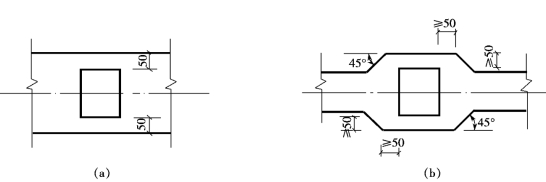
图15-68 现浇柱与条形基础梁交接处的平面尺寸

基础梁下部纵向钢筋的搭接位置宜在跨中，上部纵向钢筋的搭接位置宜在支座处，且满足搭接长度要求。顶部钢筋按计算配筋全部贯通，底部通长钢筋不应少于底部受力钢筋总截面面积的1／3。此外，纵向钢筋最小配筋率、腰筋和箍筋的设置等，应满足梁的有关构造要求。

基础梁翼板的受力钢筋，按翼板根部的弯矩配置。其受力钢筋的直径不小于8mm，间距宜为100～200mm。当翼板的悬伸长度lf＞750mm 时，其受力钢筋有一半可在距翼板边为a（a=0.5lf-20d）处切断。

条形基础的混凝土强度等级不应低于C20。