平面排架内力计算方法-从混凝土结构与砌体结构第4版中找到答案

单层厂房排架结构是个空间结构，目前，其内力计算方法有两种：考虑厂房整体空间作用和不考虑厂房整体空间作用。本节主要讨论不考虑厂房整体空间作用的平面排架的计算方法。

1）阶梯形柱的位移计算

排架是超静定结构，进行内力分析时，除了静力条件外，还需利用变形条件。由于排架柱通常是阶梯形的（最常见的是单阶柱，即上柱与下柱的截面不同）。因此，要先知道变阶柱，尤其是单阶柱位移的计算方法，才能进行排架的内力分析。

图14-36是一单阶柱柱顶受水平集中荷载作用时的位移计算简图。如图14-36中，Iu 为上柱截面惯性矩，Il 为下柱截面惯性矩，Hu 为上柱长度，Hl 为下柱长度，H 为柱全高。

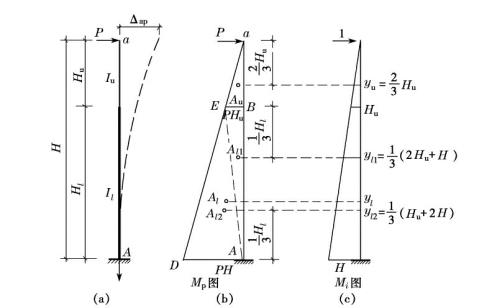
图14-36 柱顶受水平集中荷载作用时位移计算简图

由结构力学可知，柱中（截面刚度为EI）的任意一点i在外荷载作用下的位移Δip为

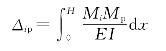
式中 Mp——外荷载作用所产生的弯矩；

Mi——在柱中计算位移的位置处作用一个与所要求的位移方向相同的单位力所产生的弯矩。

单阶柱上、下柱的截面惯性矩不相同，应进行分段积分，即

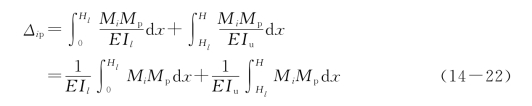
分段积分可以用分段图乘法来求解。应用图乘法在实际运算时工作量还是比较大的，为了加快计算速度，已将单阶柱在各类荷载下的位移制成了图表（附表25），设计时可直接查取。现以柱顶a作用一集中力的情况为例，简略说明计算图表的编制方法。

式中 Au、Al——分别为上、下柱Mp 图的面积，其中Al=Al1+Al2，Al1为△ABE 的面积，Al2为△ADE 的面积；

yu、yl——分别为与上、下柱Mp 图形心相对应的Mi 图的弯矩值。

于是，在柱顶作用一单位水平集中力（P=1）时（图14-37a）产生的柱顶水平位移δ（称为柱的柔度）为

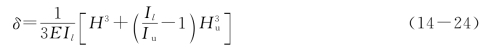
以和代入上式得

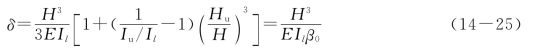
式中

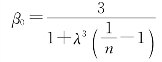
由公式（14-25）可见，单阶悬臂柱柱顶作用单位水平力时的柱顶位移值δ仅与柱的材料弹性模量、尺寸和形状有关，故称为形常数。

常用的λ、n都有一定的变化范围，将不同的λ及n 代入上式，就可以计算出β0，并绘制成计算图表，如附表25-1所示。其他荷载情况的计算图表也可用类似的方法给出，详见附表25。

由上述可见，若要使柱顶产生单位水平位移，则需要在柱顶施加1／δ的水平力（图14-37b），显然，当材料相同时，柱的截面尺寸越大，需施加的力将越大。可见1／δ反映了柱抵抗侧移的能力，一般称为侧移刚度。

2）等高排架内力计算方法——剪力分配法

对于等高的多跨排架，其内力可以简便地用剪力分配法求得。

（1）柱顶水平集中力作用下

设等高多跨排架有n 根柱（图14-38），任一柱i的侧移刚度为1／δi。根据上述的基本假定和计算简图，在柱顶水平集中力作用下，各柱顶端的位移相同，设均为Δ，即Δi=Δ（Δi 为柱i顶端的水平位移，i=1，2…n）。于是任一柱i分担的柱顶剪力Vi 为

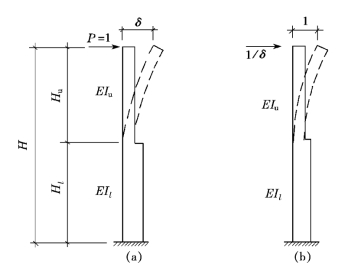
图14-37 单阶悬臂柱的侧移刚度(www.xing528.com)

由平衡条件可得

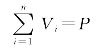
即

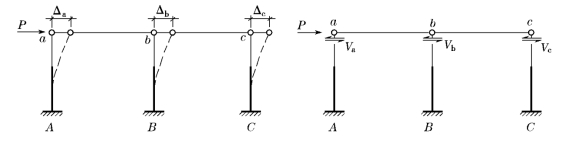
图14-38 在柱顶水平集中力作用下的剪力分配

则

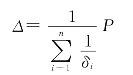
故

式中 ηi——柱i的剪力分配系数。

求得Vi 后，就可得到相应的内力图。下面对公式（14-26）的物理意义做进一步的说明。

①δi 为第i柱的柔度，（1／δi）为第i柱的侧移刚度，为第i柱的剪力分配系数，∑ηi=1。

②当排架结构柱顶作用有水平集中力P 时，各柱的柱顶剪力按其侧移刚度与各柱侧移刚度总和的比例进行分配，故称剪力分配法。

③集中力P 作用于排架的左侧或右侧时，各柱的柱顶所分配的剪力是相同的，但排架横梁的轴力将不同（轴力的符号改变，轴力的绝对值也可能改变）。

（2）在任意荷载作用下

在任意荷载作用下，等高排架的内力可按下述方法进行计算（图14-39）。图中绘示了在吊车水平荷载作用下的情况。

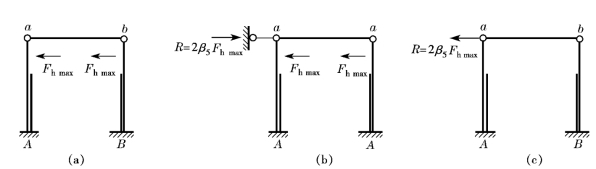
图14-39 在任意荷载作用下的剪力分配

当对称排架承受对称荷载时（如屋盖恒荷载），排架结构顶端无侧移，排架柱可简化为柱顶有不动铰支座的情况进行内力计算，如图14-40所示。

图14-40 对称排架在对称荷载作用下的内力计算

3）不等高排架内力计算方法简述

不等高排架结构在任意荷载作用下，高低列柱的柱顶水平位移不等。因此，其内力不能用剪力分配法求解。这时，用力法求解较为方便。

现以图14-41a所示高跨作用有水平集中力P 的两跨不等高排架为例来说明其内力计算方法。这时高、低跨排架横梁产生的内力为未知，分别为x1、x2。按照变形协调条件，高跨两柱的柱顶水平位移相等，低跨柱顶标高处两柱的水平位移也相等。即Δa=Δb，Δc=Δd，此处Δa、Δb、Δc、Δd 分别为a、b、c、d 点的水平位移。于是，可得到下列联立方程（图14-40b）：

式中，δa、δb、δc、δd 分别为单柱A、B、C 的柱顶a、b、c及单柱B 的结点d 处作用有单位水平力时在该处（水平力作用点）产生的水平位移；δbd、δdb分别为单位水平力作用在单柱B 结点d 处时，在B 柱柱顶b 产生的水平位移，以及单位水平力作用在单柱的柱顶b时在结点d 处产生的水平位移。按照结构力学中的位移互等定理，δbd=δdb。

显然，δa、δb、δc、δd、δbd、δdb均可按照排架柱的高度和截面尺寸用图乘法求出，解联立方程就可求得x1、x2。于是，该不等高排架结构的内力即可求得。

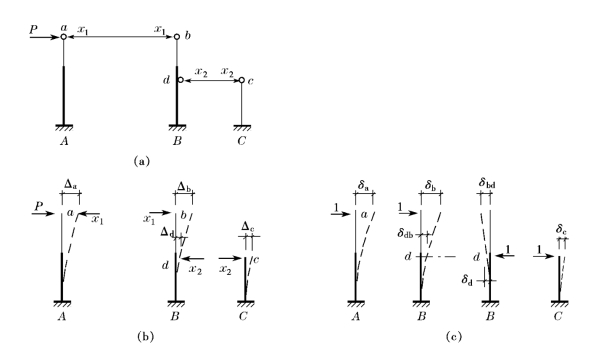
图14-41 不等高两跨排架结构的内力计算

对于其他荷载情况，其内力计算方法相同，不另赘述。