混凝土结构计算方法–非对称配筋矩形截面(第4版)

1）设计截面

当作用于构件正截面上的轴向压力设计值N（设计时取Nu=N）和弯矩设计值M（或轴向力偏心距e0）为已知，欲设计该截面时，一般可先选择混凝土强度等级和钢筋种类，确定截面尺寸，然后再计算钢筋截面面积和选用钢筋。由于混凝土强度对偏心受压构件承载力的影响比对受弯构件大，所以宜选用较高强度等级的混凝土，以便节省钢材，一般可采用C20～C40。当构件承受的荷载较小，而按刚度要求截面尺寸不宜过小时，则可适当选用较低强度等级的混凝土。纵向受力钢筋一般宜采用HRB400、HRB500和HRB335级钢筋。构造钢筋常采用HPB300级或HRB335级钢筋。箍筋采用HPB300或HRB335级钢筋。偏心受压构件除应具有一定的承载力外，还必须具有足够的刚度。因此，其截面尺寸往往是由经验（如参考类似的设计资料）或其他构造条件确定。计算钢筋截面面积时，应首先由公式（7-18）和（7-23a）求得轴向力偏心距增大系数ηns和轴向力初始偏心距ei，然后判别截面的破坏形态，最后，应用相应的公式计算钢筋截面面积和选用钢筋。

由于截面的破坏形态不仅与轴向力的偏心距有关，还与轴向力的大小、混凝土强度和钢筋强度以及配筋形式和数量有关。设计截面时，由于As 和尚未确定，所以，x 也未能确定。这时，要根据公式（7-24）来判定截面的破坏形态是困难的。理论分析结果表明，当ei＜0.3h0 时，截面总是属于小偏心受压破坏；当ei≥0.3h0 时，截面则可能属于大偏心受压破坏，也可能属于小偏心受压破坏。因此，在一般情况下，当ei＜0.3h0 时，可按小偏心受压破坏进行计算；当ei≥0.3h0 时，可先按大偏心受压破坏进行计算，然后再判断其适用条件是否满足。

（1）大偏心受压破坏

大偏心受压破坏的计算可分为两种情况。

①当钢筋As 和均为未知时

与双筋受弯构件一样，为使钢筋总用量为最少，可取x=ξbh0。于是，由公式（7-27）可得（取Nu=N）

将求得及x=ξbh0 代入公式（7-26），则得

当 时，公式（7-42）简化为

若按公式（7-41）求得的小于最小配筋率（见附表15）或为负值， 应按最小配筋率或构造要求配置。这时，As 可按为已知的情况计算。

若按公式（7-42）或（7-43）求得的As 不能满足最小配筋率的要求或为负值，As 应按最小配筋率或构造要求配置。

②当钢筋为已知时

这类问题往往是由于承受变号弯矩的需要或由于构造要求，必须在受压区配置截面面积为的钢筋，设计时应充分利用以减少As，节省用钢量。这时混凝土受压区高度x将不等于ξbh0，因此，也就不能用公式（7-42）或公式（7-43）来计算As。

为了便于计算，可将图7-17a所示计算应力图形转化为图7-17b所示的计算应力图形，这与承受弯矩M=Ne的双筋受弯截面是类似的。因此，可仿照双筋受弯截面的计算方法，将M=Ne分解为两部分，一部分是由受压钢筋的压力和相应的一部分受拉钢筋AsI的拉力fyAsI所承担的弯矩Mu1（图7-17c）；另一部分是由受压区混凝土的压力α1fcbx和相应的另一部分受拉钢筋AsⅡ的拉力fyAsⅡ及轴向力N 所承担的弯矩Mu2（图7-17d）。必须注意，图7-17c中的AsⅠ相当于图4-16中的As1，而图7-17d中的AsⅡ并不相当于图4-16中的As2，必须是才相当于图4-16中的As2。同时，AsⅡ可能为正值，也可能为负值。于是，即可按与双筋受弯截面相同的方法求得As1（即AsⅠ）和As2（即）。

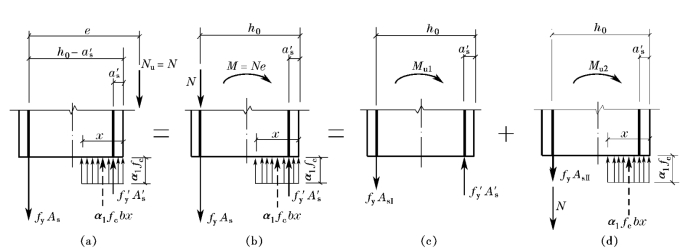
图7-17 矩形截面大偏心受压承载力计算应力图形的分解

由图7-17c可得

于是可得

或

则

这时，Mu2为已知，与Mu2相应的x 不一定等于ξbh0，因此，必须按与单筋矩形截面相同的方法求得As2，即。由此可得

因此，所必须配置的钢筋As 为

As=AsⅠ+AsⅡ

即

必须注意，在计算As2时，若求得的x＞ξbh0，则表明给定的偏少，可改按为未知的情况重新计算，使其满足x≤ξbh0；若求得的，则可仿照双筋受弯截面，直接对受压钢筋合力点取矩，以计算As，即

式中 e′——轴向力作用点到受压钢筋合力点的距离。

当所求得的很多时，还可再按不考虑受压钢筋，即取，利用公式（7-26）和公式（7-27）或采用公式（7-46）～公式（7-48）所述相同步骤求As 值，然后与按公式（7-49）所求得的As 比较，取二者之较小者来配筋。为了简化计算，也可不必进行这一计算，因二者的用钢量一般相差不多，且按公式（7-49）求得的As 是偏于安全的。

（2）小偏心受压破坏

①计算As

由公式（7-34）和公式（7-35）可见，未知数有三个，而独立的方程只有两个，故可先指定其中一个未知数。为节省钢材，应充分利用混凝土受压。于是，可按最小配筋率确定As（即取As=ρminbh，ρmin见附表15）或按构造要求确定As。

同时，为了防止离轴向力较远一侧的混凝土先发生破坏，在设计时，可配置适量的钢筋As，使截面上混凝土应力为均匀分布。因此，截面的计算应力图形将如图7-16所示，这时的初始偏心距ei 应取为（e0-ea），且偏心距增大系数η应取为1.0。由公式（7-40）可得

钢筋As 应取上述二者的较大值。

分析表明，对采用非对称配筋的小偏心受压构件，当N＞fcbh 时，应按公式（7-50）进行计算；当N≤fcbh时，按公式（7-50）计算的As 不起控制作用，故不需进行计算。

②计算

确定As 以后，可由公式（7-34）和（7-35）求得。

当混凝土强度等级不大于C50时（α1=1.0，β1=0.8），可得下列公式：

式中

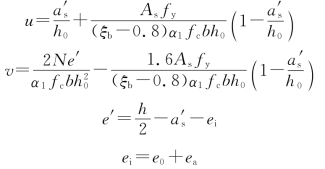
则

式中

ξ必须满足下列条件：

当 时，公式（7-53）简化为

如果上述条件不满足，表明钢筋As 已受压屈服。这时，可将原来确定的As 乘以修正系数。为区别起见，修正后的As 用Asa表示，则有

2）复核截面

复核截面时，一般已知截面尺寸b×h、混凝土强度等级、钢筋级别、钢筋截面面积As 和 以及构件计算长度l0、轴向力设计值N 及其偏心距e0，需验算截面是否能承担该轴向力。

当混凝土强度等级不大于C50时（α1=1.0，β1=0.8）其计算步骤和计算公式如下。

按公式（7-18）和公式（7-23a）确定轴向力偏心距增大系数ηns和初始偏心距ei。

当ei＜0.3h0时，按小偏心受压破坏计算。这时对轴向力N 作用点取矩可得（图7-15）

式中

于是可得

式中

则

按公式（7-57）求得的ξ必须满足公式（7-53）或公式（7-54）的要求，当ξ不能满足公式（7-53）或公式（7-54）的要求，尚应按下列公式计算：

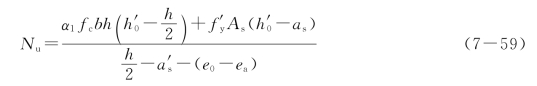
这时，截面的偏心受压承载力设计值Nu 应取按公式（7-58）和公式（7-59）的计算值的较小者。

当ei≥0.3h0 时，先按大偏心受压破坏计算。这时，对轴向力Nu 作用点取矩可得（图7-14）

(www.xing528.com)

由公式（7-60）可得

式中

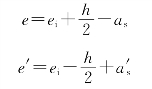
若

若，则由公式（7-30）可得

式中

若ξ＞ξb，则应按小偏心受压破坏计算。

当混凝土强度等级大于C50时，可按类似的方法推导出计算公式，此处从略。

例题7-4 某框架结构底层钢筋混凝土边柱，其上下端承受的弯矩设计值分别为（均使该柱左侧受拉），轴向力弯矩设计值N=355.5kN。已知柱计算长度l0=4.5m，柱截面尺寸为b×h=300mm×400mm。环境类别为一类，混凝土强度等级采用C30（fc=14.3N／mm2，ft=1.43N／mm2），钢筋采用HRB400级（fy=，试计算该柱所需的钢筋截面面积As 和。

解 （1）判别是否需考虑构件自身挠曲引起的附加弯矩

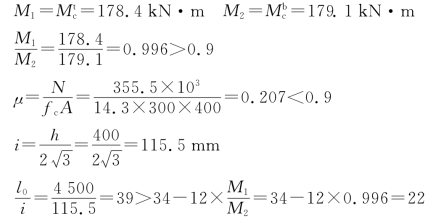
需考虑构件自身挠曲引起的附加弯矩。

（2）计算柱控制截面的弯矩设计值

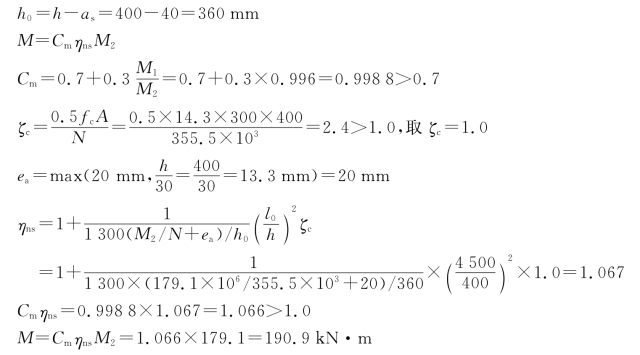
（3）配筋计算

故可先按大偏心受压破坏计算。

①计算

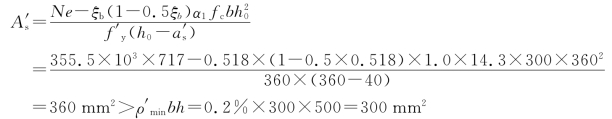
②计算As

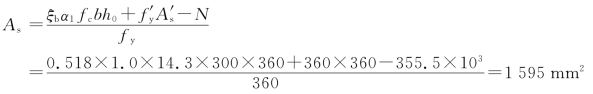
③选择钢筋

受拉钢筋选用，受压钢筋选择。

例题7-5 由于构造要求，在例题7-4中的截面上已配置受压钢筋，试计算所需的受拉钢筋截面面积As。

解 Cm、ηns、ei 等的计算与例题7-4相同。已知ei=557mm，e=717mm。As 按下述计算。

（1）计算As2

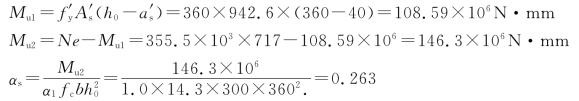
查附表16，得

则

（2）计算As

选用。

由计算结果可见，在例题7-4中，总用钢量为402+1 570=1 972mm2，在本例题中，总用钢量为942.6+1 269=2 211.6mm2，较前者用钢量增加12.2%。

例题7-6 由于构造要求，在例题7-4中的截面上已配置受压钢筋，试计算所需的受拉钢筋截面面积As。

解 Cm、ηns、ei 等的计算与例题7-4相同。已知ei=557mm，e=717mm。As 按下述计算。

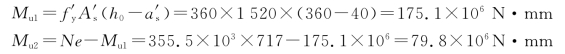
查附表16，得，表明混凝土受压区高度。

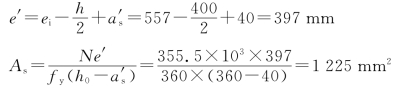
选用。

例题7-7 某框架结构钢筋混凝土柱，其上下端承受的弯矩设计值分别为（均使该柱左侧受拉），轴向力弯矩设计值N=1 386kN。已知柱计算长度l0=5.0m，柱截面尺寸为b×h=300mm×500mm，环境类别为一类。混凝土强度等级采用C30（fc=14.3N／mm2，ft=1.43N／mm2），钢筋采用HRB400级（fy=，试计算该柱所需的钢筋截面面积As 和。

解 （1）判别是否需考虑构件自身挠曲引起的附加弯矩

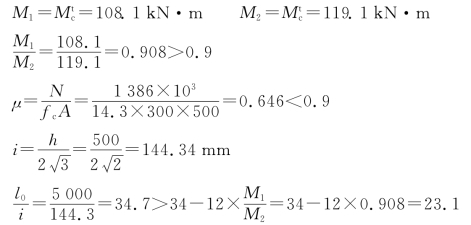
需考虑构件自身挠曲引起的附加弯矩。

（2）计算柱控制截面的弯矩设计值

（3）配筋计算

属于小偏心受压破坏。

①确定As

取As=ρminbh=0.002×300×500=300mm2，选用2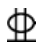14，As=308mm2

②计算

选用。

（3）验算垂直于弯矩作用平面方向的轴心受压承载力

本例从略。

例题7-8 某框架结构钢筋混凝土柱，其上下端承受的弯矩设计值分别为（均使该柱左侧受拉），轴向力弯矩设计值N=1 186kN。已知柱计算长度l0=7.0m，柱截面尺寸为b×h=400mm×600mm。环境类别为一类，混凝土强度等级采用C30（fc=14.3N／mm2，ft=1.43N／mm2），钢筋采用HRB400级试复核该截面。

解 （1）判别是否需考虑构件自身挠曲引起的附加弯矩

需考虑构件自身挠曲引起的附加弯矩。

（2）计算柱控制截面的弯矩设计值

（3）截面复核计算

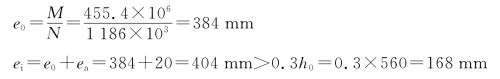
按大偏心受压破坏计算。

①计算ξ

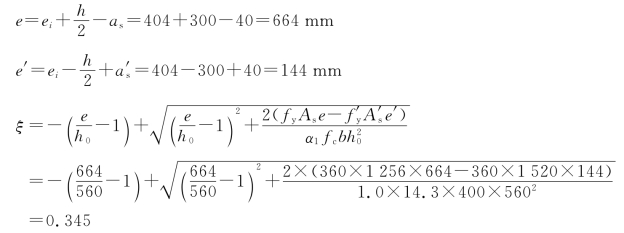
②计算Nu

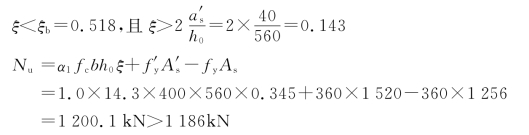
可见设计是安全和经济的。